- 2021-05-08 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级下册数学教案 30-4 第1课时 抛物线形问题 冀教版
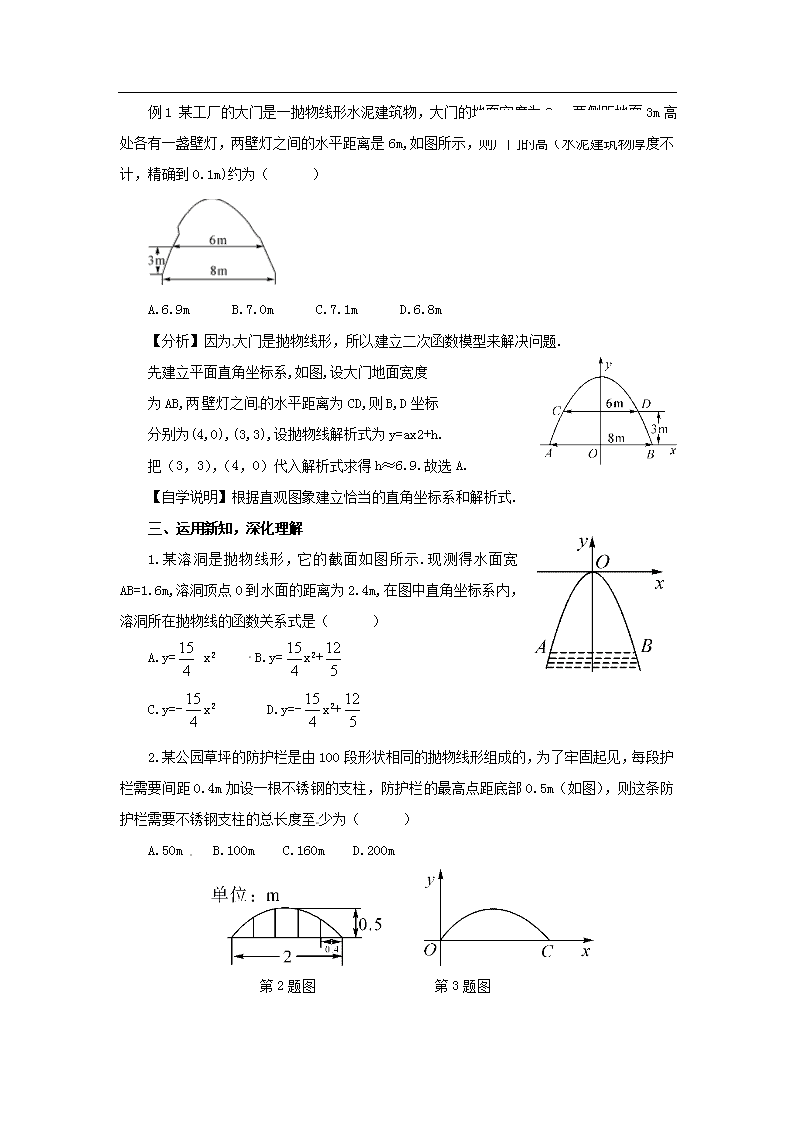
30.4 二次函数的应用 第1课时 抛物线形问题 学习目的 【知识与技能】 能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能利用二次函数的知识解决实际问题. 【过程与方法】 经历运用二次函数解决实际问题的探究过程,进一步体验运用数学方法描述变量之间的依赖关系,体会二次函数是解决实际问题的重要模型,提高运用数学知识解决实际问题的能力. 【情感态度】 1.体验函数是有效的描述现实世界的重要手段,认识到数学是解决问题和进行交流的重要工具. 2.敢于面对在解决实际问题时碰到的困难,积累运用知识解决问题的成功经验. 【学习重点】 用抛物线的知识解决拱桥类问题.[来源:学+科+网Z+X+X+K] 【学习难点】 将实际问题转化为抛物线的知识来解决. 自学过程 一、情境导入,初步认识 1、如图所示的抛物线的解析式可设为 ,若AB∥x轴,且AB=4,OC=1,则点A的坐标为 ,点B的坐标为 ;代入解析式可得出此抛物线的解析式为 . 2、 某涵洞是抛物线形,它的截面如图所示。现测得水面宽AB=4m,涵洞顶点O到水面的距离为1m,于是你可推断点A的坐标是 ,点B的坐标为 ;根据图中的直角坐标系内,涵洞所在的抛物线的函数解析式可设为 . 二、思考探究,获取新知 探究 直观图象的建模应用[来源:Z。xx。k.Com] 例1 某工厂的大门是一抛物线形水泥建筑物,大门的地面宽度为8m,两侧距地面3m高处各有一盏壁灯,两壁灯之间的水平距离是6m,如图所示,则厂门的高(水泥建筑物厚度不计,精确到0.1m)约为( ) A.6.9m B.7.0m C.7.1m D.6.8m 【分析】因为大门是抛物线形,所以建立二次函数模型来解决问题.[来源:学科网ZXXK] 先建立平面直角坐标系,如图,设大门地面宽度 为AB,两壁灯之间的水平距离为CD,则B,D坐标 分别为(4,0),(3,3),设抛物线解析式为y=ax2+h. 把(3,3),(4,0)代入解析式求得h≈6.9.故选A. 【自学说明】根据直观图象建立恰当的直角坐标系和解析式. 三、运用新知,深化理解 1.某溶洞是抛物线形,它的截面如图所示.现测得水面宽AB=1.6m,溶洞顶点O到水面的距离为2.4m,在图中直角坐标系内,溶洞所在抛物线的函数关系式是( ) A.y= x2 B.y=x2+ C.y=-x2 D.y=-x2+[来源:学科网ZXXK] 2.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( ) A.50m B.100m C.160m D.200m [来源:学科网] 第2题图 第3题图 3.如图,济南建邦大桥有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需 秒. 四、预习小结 你学到了什么?还有哪些疑惑? 建立二次实际问题的一般步骤:(1)根据题意建立适当的平面直角坐标系.(2)把已知条件转化为点的坐标.(3)合理设出函数解析式.(4)利用待定系数法求出函数解析式.(5)根据求得的解析式进一步分析,判断并进行有关的计算.查看更多