- 2021-05-08 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
甘肃省张掖市山丹县第一中学2019-2020学年高一11月月考数学试题
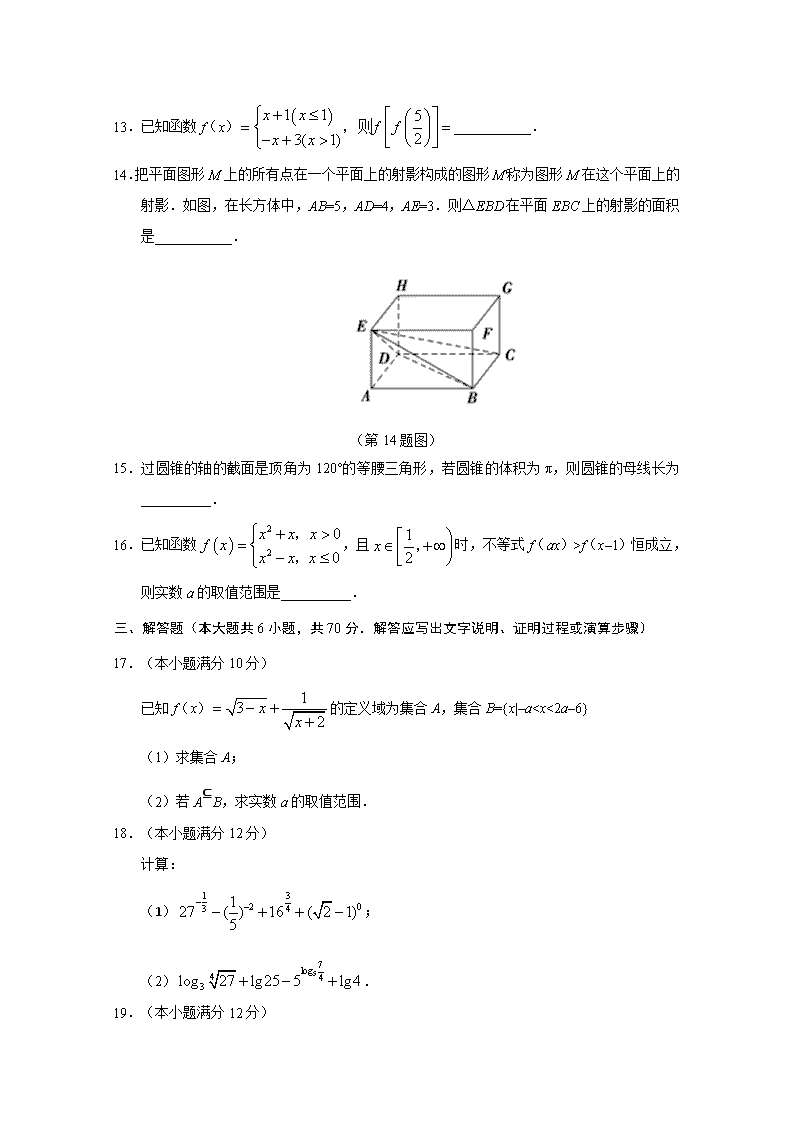
山丹一中2019-2020学年上学期11月月考试卷 高一数学 (考试时间:120分钟 试卷满分:150分) 测试范围:人教必修1,必修2第1章、第2章。 第Ⅰ卷 一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设集合A={x|–3≤x<1},B={x|x2≤4},则A∪B等于 A.{x|–2≤x<1} B.{x|–3≤x≤2} C.{x|x<1} D.{x|x≤2} 2.函数f(x)的定义域为 A.{x|x≥–3且x≠–1} B.{x|x>–3且x≠–1} C.{x|x≥–1} D.{x|x≥–3} 3.下列关于棱柱的说法中,错误的是 A.三棱柱的底面为三角形 B.一个棱柱至少有五个面 C.若棱柱的底面边长相等,则它的各个侧面全等 D.五棱柱有5条侧棱、5个侧面,侧面为平行四边形 4.已知f(x)=ax5+bx3+cx+3,且f(–2)=5,则f(2)= A.2 B.1 C.–2 D.–1 5.已知函数f(2)=x+45,则f(x)的解析式为 A.f(x)=x2+1 B.f(x)=x2+1(x≥2) C.f(x)=x2 D.f(x)=x2(x≥2) 6.下列命题正确的是 A.有两个面互相平行,其余四个面都是等腰梯形的六面体为棱台 B.用一个平面去截棱锥,棱锥底面和截面之间的部分为棱台 C.棱锥是由一个底面为多边形,其余各面为具有公共顶点的三角形围成的几何体 D.一个正方形按不同方向平移所得几何体都是正方体 7.函数y的定义域为R,则k的取值范围是 A.(–∞,9)∪[0,+∞) B.[1,+∞) C.[–9,1) D.(0,1] 8.A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对折裁剪后可以得到2张A1纸,1张A1纸对折裁剪可以得到2张A2纸,依此类推.这是因为A系列纸张的长宽比为:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41,那么A4纸的长度为 A.14.8厘米 B.21.0厘米 C.29.7厘米 D.42.0厘米 9.若函数f(x)=loga(x2–ax+2)在区间(0,1]上单调递减,则实数a的取值范围是 A.[2,3) B.(2,3) C.[2,+∞) D.(2,+∞) 10.某工厂产生的废气经过过滤后排放,规定排放时污染物的残留含量不德超过1%,已知在过滤过程中的污染物的残留数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为:P=P0•e–kt(k为正的常数,P0为原污染物数量).若前5个小时废气中的污染物被过滤掉了90%,那么要能够按规定排放废气,至少还需要过滤 A.小时 B.小时 C.5小时 D.小时 11.设函数f(x)满足f()=1+x,则f(x)的表达式为 A. B. C. D. 12.已知函数f(x)=ln(1+|x|),则关于x的不等式f(lnx)+f(ln)<2f(1)的解集为 A.(0,+∞) B.(0,e) C.(,e) D.(1,e) 第Ⅱ卷 二、填空题(本题共4小题,每小题5分,共20分) 13.已知函数f(x)___________. 14.把平面图形M上的所有点在一个平面上的射影构成的图形M'称为图形M在这个平面上的射影.如图,在长方体中,AB=5,AD=4,AE=3.则△EBD在平面EBC上的射影的面积是___________. (第14题图) 15.过圆锥的轴的截面是顶角为120°的等腰三角形,若圆锥的体积为π,则圆锥的母线长为__________. 16.已知函数,且时,不等式f(ax)>f(x–1)恒成立,则实数a的取值范围是__________. 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分) 已知f(x)的定义域为集合A,集合B={x|–a查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档