- 2021-05-06 发布 |
- 37.5 KB |
- 6页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2015年高考试题——数学理(北京卷)原卷版
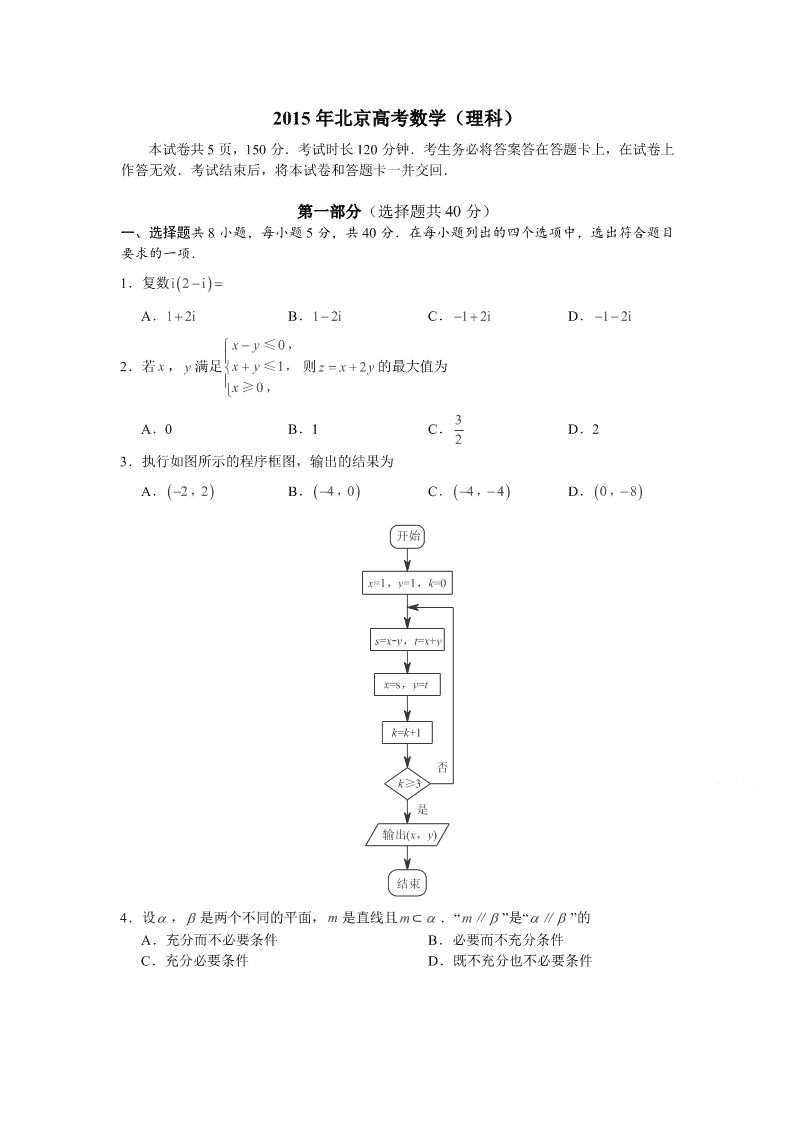
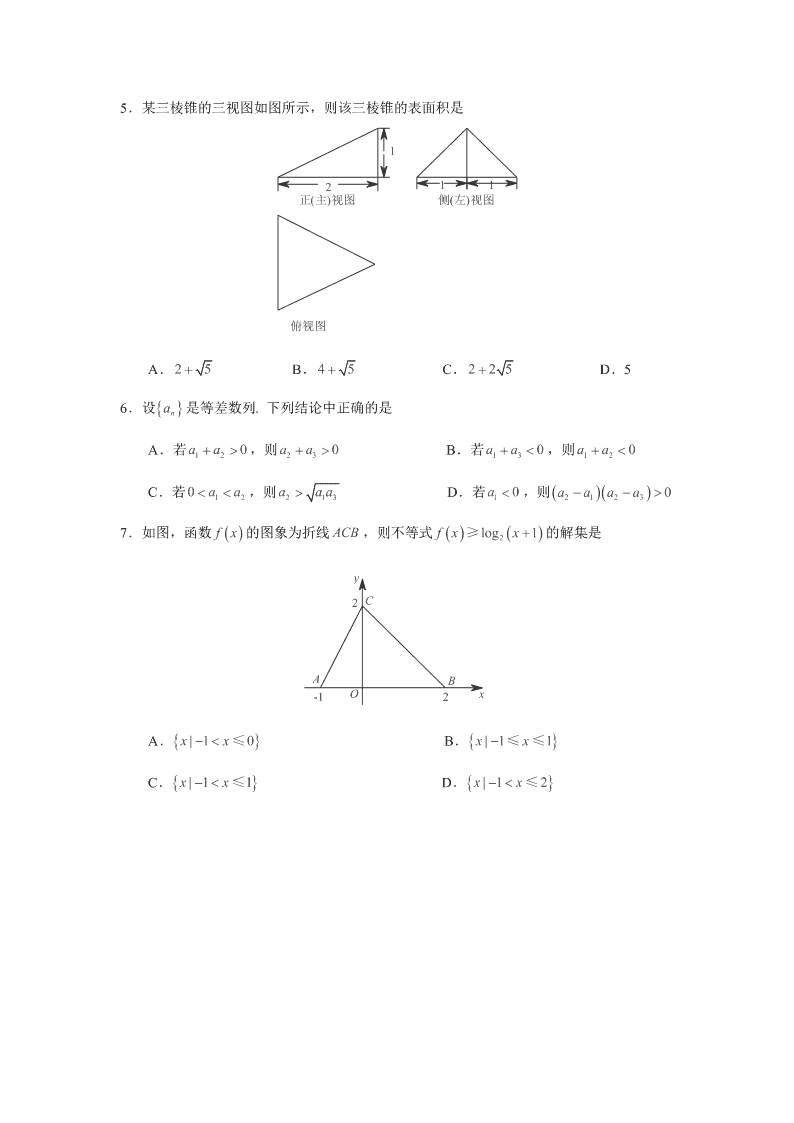
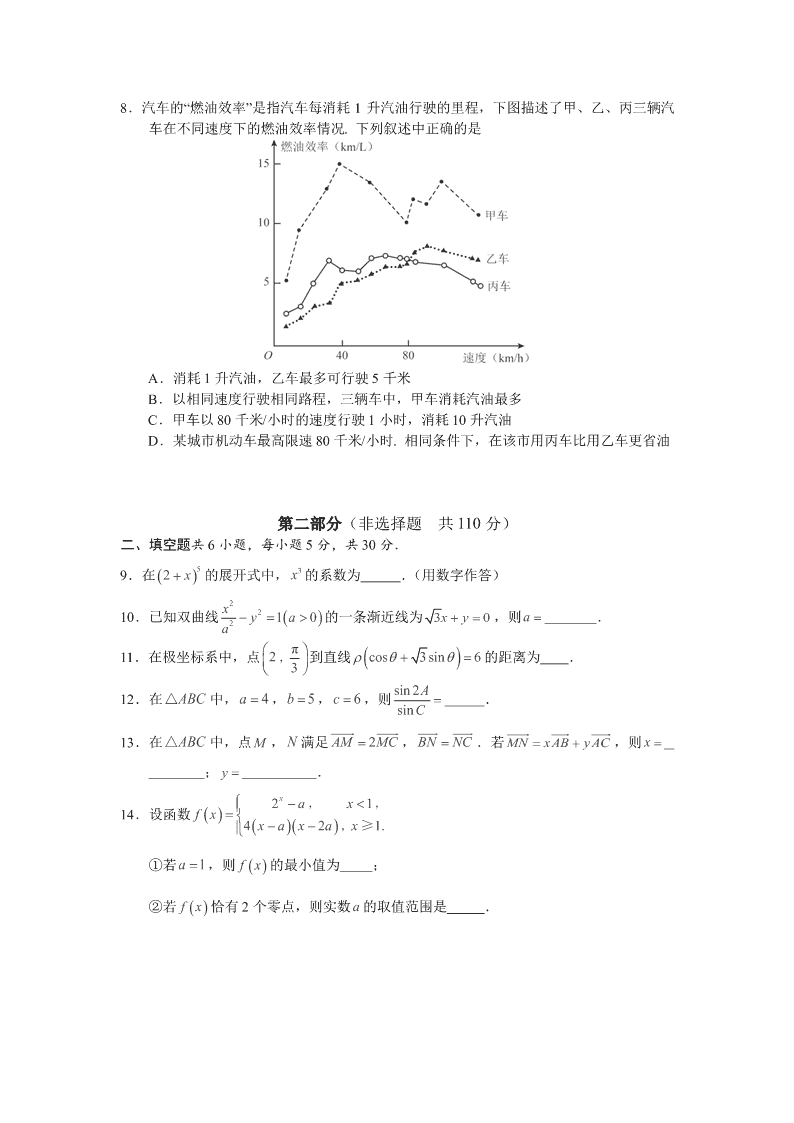
2015 年北京高考数学(理科) 本试卷共 5 页,150 分.考试时长 120 分钟.考生务必将答案答在答题卡上,在试卷上 作答无效.考试结束后,将本试卷和答题卡一并交回. 第一部分(选择题共 40 分) 一、选择题共 8 小题,每小题 5 分,共 40 分.在每小题列出的四个选项中,选出符合题目 要求的一项. 1.复数 i 2 i A.1 2i B.1 2i C. 1 2i D. 1 2i 2.若 x , y 满足 0 1 0 xy xy x ≤ , ≤ , ≥ , 则 2z x y 的最大值为 A.0 B.1 C. 3 2 D.2 3.执行如图所示的程序框图,输出的结果为 A. 22 , B. 40 , C. 44, D. 08, 开始 x=1,y=1,k=0 s=x-y,t=x+y x=s,y=t k=k+1 k≥3 输出(x,y) 结束 是 否 4.设 , 是两个不同的平面, m 是直线且 m ⊂ .“ m ∥ ”是“∥ ”的 A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 5.某三棱锥的三视图如图所示,则该三棱锥的表面积是 正(主)视图 11 俯视图 侧(左)视图 2 1 A. 25 B. 45 C. 2 2 5 D.5 6.设 na 是等差数列. 下列结论中正确的是 A.若 120aa,则 230aa B.若 130aa,则 120aa C.若 120 aa,则 2 1 3a a a D.若 1 0a ,则 2 1 2 3 0a a a a 7.如图,函数 fx的图象为折线 ACB ,则不等式 2log 1f x x ≥ 的解集是 A B O x y -1 2 2 C A. | 1 0xx ≤ B. | 1 1xx ≤ ≤ C. | 1 1xx ≤ D. | 1 2xx ≤ 8.汽车的“燃油效率”是指汽车每消耗 1 升汽油行驶的里程,下图描述了甲、乙、丙三辆汽 车在不同速度下的燃油效率情况. 下列叙述中正确的是 A.消耗 1 升汽油,乙车最多可行驶 5 千米 B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多 C.甲车以 80 千米/小时的速度行驶 1 小时,消耗 10 升汽油 D.某城市机动车最高限速 80 千米/小时. 相同条件下,在该市用丙车比用乙车更省油 第二部分(非选择题 共 110 分) 二、填空题共 6 小题,每小题 5 分,共 30 分. 9.在 52 x 的展开式中, 3x 的系数为 .(用数字作答) 10.已知双曲线 2 2 2 10x yaa 的一条渐近线为 30xy,则 a . 11.在极坐标系中,点 π2 3 ‚ 到直线 cos 3sin 6 的距离为 . 12.在 ABC△ 中, 4a , 5b , 6c ,则 sin 2 sin A C . 13.在 ABC△ 中,点 M , N 满足 2AM MC , BN NC .若 MN xAB y AC,则 x ; y . 14.设函数 21 4 2 1. x axfx x a x a x ‚ ‚ ‚ ≥ ①若 1a ,则 fx的最小值为 ; ②若 fx恰有 2 个零点,则实数 a 的取值范围是 . 三、解答题(共 6 小题,共 80 分.解答应写出文字说明,演算步骤或证明过程) 15.(本小题 13 分) 已知函数 2( ) 2 sin cos 2 sin2 2 2 x x xfx. (Ⅰ) 求 ()fx的最小正周期; (Ⅱ) 求 ()fx在区间[ π 0] , 上的最小值. 16.(本小题 13 分) A , B 两组各有 7 位病人,他们服用某种药物后的康复时间(单位:天)记录如下: A 组:10,11,12,13,14,15,16 B 组:12,13,15,16,17,14, a 假设所有病人的康复时间互相独立,从 A , B 两组随机各选 1 人, A 组选出的人记为 甲, B 组选出的人记为乙. (Ⅰ) 求甲的康复时间不少于 14 天的概率; (Ⅱ) 如果 25a ,求甲的康复时间比乙的康复时间长的概率; (Ⅲ) 当 a 为何值时, A , B 两组病人康复时间的方差相等?(结论不要求证明) 17.(本小题 14 分) 如图,在四棱锥 A EFCB 中, AEF△ 为等边三角形,平面 AEF 平面 EFCB , EF BC∥ , 4BC , 2EF a , 60EBC FCB ,O 为 EF 的中点. (Ⅰ) 求证: AO BE ; (Ⅱ) 求二面角 F AE B的余弦值; (Ⅲ) 若 BE 平面 AOC ,求 a 的值. O F E C B A 18.(本小题 13 分) 已知函数 1ln1 xfx x . (Ⅰ)求曲线 y f x 在点 00f, 处的切线方程; (Ⅱ)求证:当 01x , 时, 3 2 3 xf x x ; (Ⅲ)设实数 k 使得 3 3 xf x k x 对 01x , 恒成立,求 k 的最大值. 19.(本小题 14 分) 已知椭圆C : 22 2210xy abab 的离心率为 2 2 ,点 01P , 和点 A m n, 0m≠ 都 在椭圆C 上,直线 PA 交 x 轴于点 M . (Ⅰ)求椭圆C 的方程,并求点 M 的坐标(用 m , n 表示); (Ⅱ)设 O 为原点,点 B 与点 A 关于 x 轴对称,直线 PB 交 x 轴于点 N .问: y 轴上是 否存在点Q ,使得 OQM ONQ ?若存在,求点Q 的坐标;若不存在,说明理由. 20.(本小题 13 分) 已知数列 na 满足: * 1a N , 1 36a ≤ ,且 1 2 18 2 36 18 nn n nn aaa aa , ≤ , , 12n , , . 记集合 *|nM a nN . (Ⅰ)若 1 6a ,写出集合 M 的所有元素; (Ⅱ)若集合 M 存在一个元素是 3 的倍数,证明: M 的所有元素都是 3 的倍数; (Ⅲ)求集合 M 的元素个数的最大值. (考生务必将答案答在答题卡上,在试卷上作答无效)查看更多