人教版九年级数学上册专题训练(十一)证明圆的切线的两种常见方法

人教版九年级数学上册专题训练(十一)证明圆的切线的两种常见方法

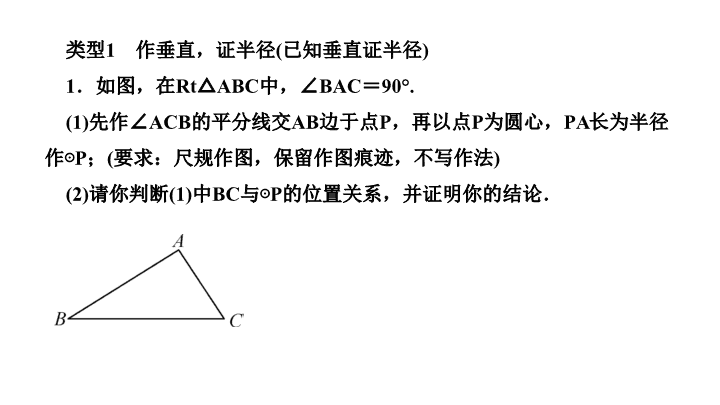
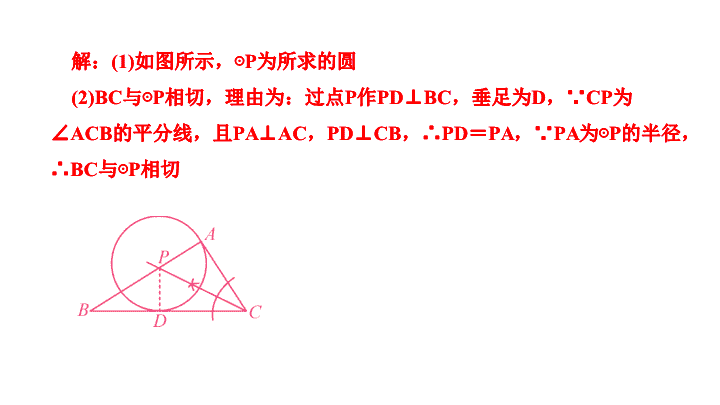
第二十四章　圆 人教版 专题训练(十一)　 证明圆的切线的两种常见方法 类型 1 　作垂直，证半径 ( 已知垂直证半径 ) 1 ．如图，在 Rt△ABC 中，∠ BAC ＝ 90°. (1) 先作∠ ACB 的平分线交 AB 边于点 P ，再以点 P 为圆心， PA 长为半径作⊙ P ； ( 要求：尺规作图，保留作图痕迹，不写作法 ) (2) 请你判断 (1) 中 BC 与⊙ P 的位置关系，并证明你的结论． 解： (1) 如图所示，⊙ P 为所求的圆 (2)BC 与⊙ P 相切，理由为：过点 P 作 PD⊥BC ，垂足为 D ，∵ CP 为∠ ACB 的平分线，且 PA⊥AC ， PD⊥CB ，∴ PD ＝ PA ，∵ PA 为⊙ P 的半径，∴ BC 与⊙ P 相切 解： (1) 如图所示，⊙ P 为所求的圆 (2)BC 与⊙ P 相切，理由为：过点 P 作 PD⊥BC ，垂足为 D ，∵ CP 为∠ ACB 的平分线，且 PA⊥AC ， PD⊥CB ，∴ PD ＝ PA ，∵ PA 为⊙ P 的半径，∴ BC 与⊙ P 相切 2 ．如图， O 为正方形 ABCD 对角线 AC 上一点，以点 O 为圆心， OA 长为半径的⊙ O 与 BC 相切于点 M. 求证： CD 与⊙ O 相切． 证明：连接 OM ，过点 O 作 ON⊥CD 于点 N ，∵四边形 ABCD 是正方形，∴∠ BCD ＝ 90° ， AC 平分∠ BCD ，∵⊙ O 与 BC 相切，∴ OM⊥BC ，又∵ ON⊥CD ，∴ OM ＝ ON ，∴ ON 是⊙ O 的半径，∴ CD 与⊙ O 相切 类型 2 　连半径，证垂直 ( 已知半径证垂直 ) ( 一 ) 利用勾股定理证垂直 3 ．如图， AB 为⊙ O 的直径，点 P 为 AB 延长线上一点，点 C 为⊙ O 上一点， PC ＝ 8 ， PB ＝ 4 ， AB ＝ 12 ，求证： PC 是⊙ O 的切线． 证明：如图，连接 OC ，∵ AB ＝ 12 ，∴ OA ＝ OB ＝ OC ＝ 6 ，∴ OP ＝ OB ＋ BP ＝ 6 ＋ 4 ＝ 10. 在△ OPC 中，∵ OP ＝ 10 ， PC ＝ 8 ， OC ＝ 6 ， 6 2 ＋ 8 2 ＝ 10 2 ，即 CO 2 ＋ PC 2 ＝ OP 2 ，∴△ OPC 为直角三角形，∠ OCP ＝ 90° ，∵点 C 在⊙ O 上，∴ PC 是⊙ O 的切线 ( 二 ) 利用全等证垂直 4 ．如图，已知 AB 是⊙ O 的直径， BC⊥AB ，连接 OC ，弦 AD∥OC ，直线 CD 交 BA 的延长线于点 E. 求证：直线 CD 是⊙ O 的切线． 证明：连接 DO.∵AD∥OC ，∴∠ DAO ＝∠ COB ，∠ ADO ＝∠ COD. 又∵ OA ＝ OD ，∴∠ DAO ＝∠ ADO ，∴∠ COD ＝∠ COB.∵OC ＝ OC ， OD ＝ OB ，∴△ COD≌△COB(SAS) ，∴∠ CDO ＝∠ CBO ＝ 90°. 又∵点 D 在⊙ O 上，∴ CD 是⊙ O 的切线 ( 三 ) 利用角度转换证垂直 5 ． ( 鄂尔多斯中考改编 ) 如图， AB 是⊙ O 的直径，弦 CD⊥AB ，垂足为 H ，连接 AC. 过上一点 E 作 EG∥AC 交 CD 的延长线于点 G ，连接 AE 交 CD 于点 F ，且 EG ＝ FG. 求证： EG 是⊙ O 的切线； 证明：连接 OE ，如图，∵ GE ＝ GF ，∴∠ GEF ＝∠ GFE ，而∠ GFE ＝∠ AFH ，∴∠ GEF ＝∠ AFH ，∵ AB⊥CD ，∴∠ OAF ＋∠ AFH ＝ 90° ，∴∠ GEA ＋∠ OAF ＝ 90° ，∵ OA ＝ OE ，∴∠ OEA ＝∠ OAF ，∴∠ GEA ＋∠ OEA ＝ 90° ，即∠ GEO ＝ 90° ，∴ OE⊥GE ，∴ EG 是⊙ O 的切线 证明：连接 OE ，如图，∵ GE ＝ GF ，∴∠ GEF ＝∠ GFE ，而∠ GFE ＝∠ AFH ，∴∠ GEF ＝∠ AFH ，∵ AB⊥CD ，∴∠ OAF ＋∠ AFH ＝ 90° ，∴∠ GEA ＋∠ OAF ＝ 90° ，∵ OA ＝ OE ，∴∠ OEA ＝∠ OAF ，∴∠ GEA ＋∠ OEA ＝ 90° ，即∠ GEO ＝ 90° ，∴ OE⊥GE ，∴ EG 是⊙ O 的切线