2019届二轮复习函数、导数与不等式的提分策略学案(全国通用)
函数、导数与不等式的提分策略
授课提示:对应学生用书第16页
提分策略一 “双图法——明确思路”
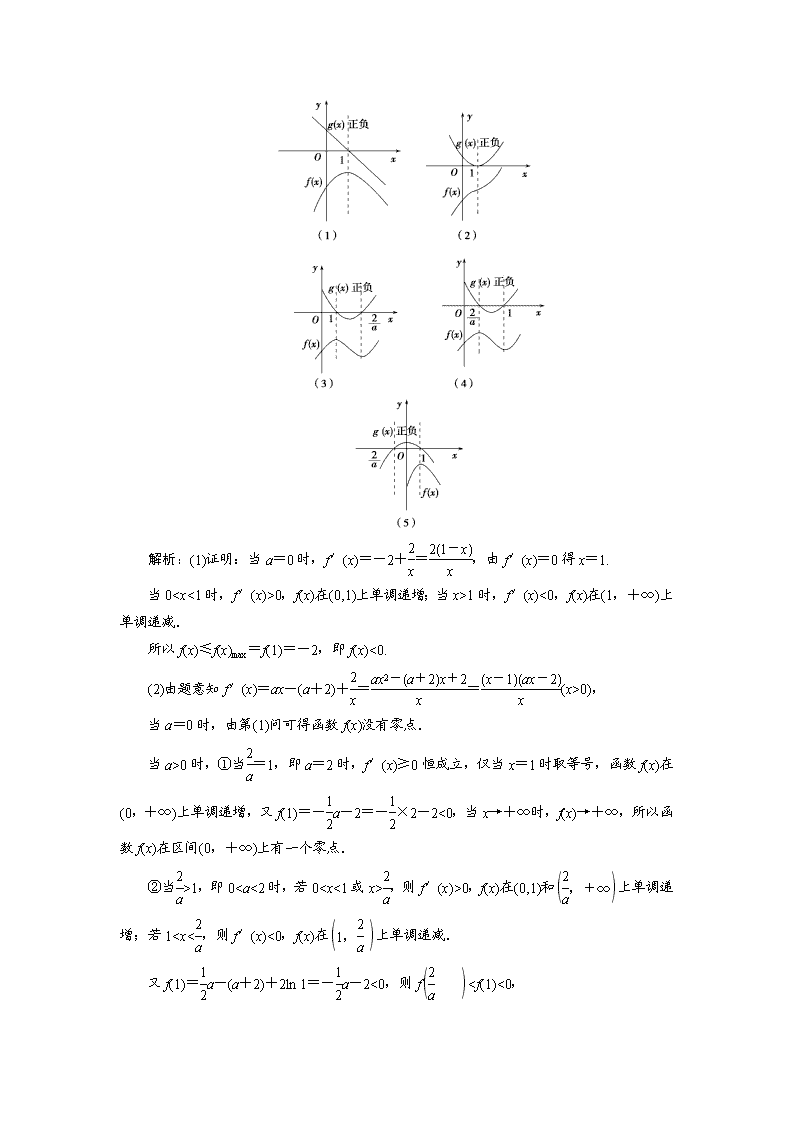
在解答函数综合问题时,若能快速地画出相关函数的图象,便可直观明快地解决问题.然而,画函数f(x)的图象前,需要明确其单调性(走势)、极值、最值及端点值.尤其是单调性,对于可导函数,单调性由导数f′(x)的正负确定,于是我们从f′(x)中“抽象”出与其正负相关的函数g(x),通过g(x)的图象(只需关注其正负值)即可大致画出f(x)的图象,通过g(x)与f(x)的图象解决问题的方法,我们称其为“双图法”.
已知函数f(x)=ax2-(a+2)x+2ln x(a∈R).
(1)若a=0,求证:f(x)<0;
(2)讨论函数f(x)零点的个数.
分析:(1)当a=0时,f(x)=-2x+2ln x(x>0),f′(x)=-2+=,设g(x)=1-x,根据g(x)的正负可画出f(x)的图象如图(1)所示.(2)f′(x)=(x>0),令g(x)=(x-1)(ax-2),当a=0时,由(1)知f(x)没有零点;当a>0时,画g(x)的正负图象时,需分=1,>1,<1三种情形进行讨论,再根据极值、端点走势可画出f(x)的图象,如图(2)(3)(4)所示;当a<0时,同理可得图(5).综上,易得f(x)的零点个数.
解析:(1)证明:当a=0时,f′(x)=-2+=,由f′(x)=0得x=1.
当0
0,f(x)在(0,1)上单调递增;当x>1时,f′(x)<0,f(x)在(1,+∞)上单调递减.
所以f(x)≤f(x)max=f(1)=-2,即f(x)<0.
(2)由题意知f′(x)=ax-(a+2)+==(x>0),
当a=0时,由第(1)问可得函数f(x)没有零点.
当a>0时,①当=1,即a=2时,f′(x)≥0恒成立,仅当x=1时取等号,函数f(x)在(0,+∞)上单调递增,又f(1)=-a-2=-×2-2<0,当x→+∞时,f(x)→+∞,所以函数f(x)在区间(0,+∞)上有一个零点.
②当>1,即0,则f′(x)>0,f(x)在(0,1)和上单调递增;若12时,若01,则f′(x)>0,f(x)在和(1,+∞)上单调递增;
若2,所以f=--2+2ln <--2+2ln 1<0,
又x→+∞时,f(x)→+∞,
所以函数f(x)仅有一个零点在区间(1,+∞)上.
当<0,即a<0时,若00,f(x)在(0,1)上单调递增;
若x>1,f′(x)<0,f(x)在(1,+∞)上单调递减.
当x→0时,f(x)→-∞,当x→+∞时,f(x)→-∞,
又f(1)=a-(a+2)+2ln 1=-a-2=.
当f(1)=>0,即a<-4时,函数f(x)有两个零点;
当f(1)==0,即a=-4时,函数f(x)有一个零点;
当f(1)=<0,即-40时,函数f(x)有一个零点.
点评 解决本题运用了分类、分层的思想方法,表面看起来非常繁杂.但若能用好“双图法”处理问题,可回避不等式f′(x)>0与f′(x)<0的求解,特别是含有参数的不等式求解,而从f′(x)抽象出与其正负有关的函数g(x),画图更方便,观察图形即可直观快速地得到f(x)的单调性,大大提高解题的效率.
[对点训练]
已知函数f(x)=ex(2x-1)-ax+a(a∈R),e为自然对数的底数.
(1)当a=1时,求函数f(x)的单调区间;
(2)①若存在实数x,满足f(x)<0,求实数a的取值范围;
②若有且只有唯一整数x0,满足f(x0)<0,求实数a的取值范围.
解析:(1)当a=1时,f(x)=ex(2x-1)-x+1,f′(x)=ex(2x+1)-1,f′(0)=0,f″(x)=ex(2x+3),
由f″(x)=0,得x=-,当x<-时,f″(x)<0,f′(x)单调递减;当x>-时,f″(
x)>0,f′(x)单调递增.且当x<-时,f′(x)<0,即当x<0时,f′(x)<0,f(x)单调递减;当x>0时,f′(x)>0,f(x)单调递增.
所以f(x)的单调减区间为(-∞,0),单调增区间为(0,+∞).
(2)①由f(x)<0,得ex(2x-1)1时,a>;
当x<1时,a<.
记g(x)=,
g′(x)==,
所以g(x)在区间(-∞,0)和上为增函数,在(0,1)和上为减函数.
所以当x>1时,a>g=4e;当x<1时,aa,
又g(x)在区间(-∞,0)上单调递增,在(0,1)上单调递减,且g(0)=1>a,所以g(-1)≤a,即a≥,所以≤a<1.
当a>4e时, x0∈(1,+∞),由f(x0)<0,得g(x0)f
B.f>2f(1)cos 1
C.2f(1)cos 1>f
D.f0,cos x>0,构造函数F(x)=f(x)cos x,
则F′(x)=-f(x)sin x+f′(x)cos x,
因为对任意的x∈,不等式f(x)tan x0恒成立,
所以F′(x)>0恒成立,所以函数F(x)在x∈上单调递增,
所以F0时,<0恒成立,则不等式>0的解集为( )
A.(-2,0)∪(2,+∞)
B.(-2,0)∪(0,2)
C.(-∞,-2)∪(0,2)
D.(-∞,-2)∪(2,+∞)
解析:设g(x)=,则g′(x)=′=,当x>0时,g′(x)<0,所以函数g(x)=在(0,+∞)上单调递减.因为f(x)是奇函数,所以g(x)=是偶函数.因为f(2)=0,所以f(-2)=0.所以不等式>0的解集为(-2,0)∪(0,2). 故选B.
答案:B
3.构造F(x)=enxf(x)(n∈Z,且n≠0)类型的辅助函数
已知f(x)(x∈R)有导函数,且∀x∈R,f′(x)>f(x),n∈N*,则有( )
A.enf(-n)enf(0)
B.enf(-n)f(0),f(n)>enf(0)
D.enf(-n)>f(0),f(n)0,g(x)为R上的增函数,故g(-n)enf(0),故选A.
答案:A
点评 构造函数解决导数问题常用模型
(1)条件:f′(x)>a(a≠0) 构造函数:h(x)=f(x)-ax
(2)条件:f′(x)±g′(x)>0 构造函数:h(x)=f(x)±g(x)
(3)条件:f′(x)+f(x)>0 构造函数:h(x)=exf(x)
(4)条件:f′(x)-f(x)>0 构造函数:h(x)=
(5)条件:xf′(x)+f(x)>0 构造函数:h(x)=xf(x)
(6)条件:xf′(x)-f(x)>0 构造函数:h(x)=
[对点训练]
1.已知f(x)的定义域为(0,+∞),f′(x)为f(x)的导函数,且满足f(x)<-xf′(x),则不等式f(x+1)>(x-1)f(x2-1)的解集是( )
A.(0,1) B.(1,+∞)
C.(1,2) D.(2,+∞)
解析:因为f(x)<-xf′(x),所以f(x)+xf′(x)<0,即(xf(x)) ′<0,所以函数y=xf(x)在(0,+∞)上单调递减.由不等式f(x+1)>(x-1)f(x2-1),可得(x+1)f(x+1)>(x2-1)f(x2-1),所以解得x>2.选D.
答案:D
2.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且2f(x)+xf′(x)>x2,则不等式(x+2 016)2f(x+2 016)-4f(-2)>0的解集为( )
A.(-∞,-2 016) B.(-∞,-2 018)
C.(-2 018,0) D.(-2 016,0)
解析:由2f(x)+xf′(x)>x2,结合x∈(-∞,0)得2xf(x)+x2f′(x)0可化为(x+2 016)2f(x+2 016)>(-2)2f(-2),
所以解得x<-2 018.故选B.
答案:B
二、构造函数证明不等式问题常见类型
1.选择关键部分来构造
设函数f(x)=x2ex-1+ax3+bx2,已知x=-2和x=1为f(x)的极值点.
(1)求a,b值;
(2)讨论f(x)的单调性;
(3)设g(x)=x3-x2,比较f(x)与g(x)的大小.
解析:(1)由已知得f′(x)=2xex-1+x2ex-1+3ax2+2bx=xex-1(x+2)+x(3ax+2b),
由x=-2和x=1为f(x)的极值点,得
,
即,
解得.
(2)由(1)得f′(x)=x(x+2)(ex-1-1).
令f′(x)=0,得x1=-2,x2=0,x3=1.
f′(x)、f(x)随x的变化情况如下表:
x
(-∞,-2)
-2
(-2,0)
0
(0,1)
1
(1,+∞)
f′(x)
-
0
+
0
-
0
+
f(x)
极小值
极大值
极小值
从表可知:函数f(x)在(-2,0)和(1,+∞)上单调递增,在(-∞,-2)和(0,1)上单调递减.
(3)由(1)可知f(x)=x2ex-1-x3-x2,故f(x)-g(x)=x2ex-1-x3=x2(ex-1-x).
选取关键部分构造,可令h(x)=ex-1-x,则h′(x)=ex-1-1,令h′(x)=0得x=1;因为当x∈(-∞,1]时,h′(x)≤0,所以h(x)在(-∞,1]上单调递减;故当x∈(-∞,1]时,h(x)≥h(1)=0;因为当x∈[1,+∞)时,h′(x)≥0,所以h(x)在[1,+∞)上单调递增;故x∈[1,+∞)时,h(x)≥h(1)=0.所以对任意x∈(-∞,+∞),恒有h(x)≥0;又x2≥0,因此f(x)-g(x)≥0;故对任意x∈(-∞,+∞),恒有f(x)≥g(x).
点评 所谓选择关键部分,就是在差函数f(x)-g(x)=x2ex-1-x3=x2(ex-1-x)中,x2已经能够明确地判断符号,为了求导简单,没有必要一起构造,只需要选择关键部分ex-1-x构造即可.
2.适当放缩再构造
已知函数f(x)=+aln(x-1),其中n∈N*,a为常数.
(1)当n=2时,求函数f(x)的极值;
(2)当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
解析:(1)f(x)的定义域为{x|x>1}.当n=2时:当a>0时,f(x)的极小值为f=;当a≤0时f(x)无极值.
(2)证明:法一:令g(x)=x-1--ln(x-1),则g′(x)=1+-=+(x≥2).
讨论:若n为偶数,则当x∈[2,+∞)时,g′(x)>0,g(x)单调递增;又g(2)=0,因此g(x)=x-1--ln(x-1)≥g(2)=0恒成立,所以f(x)≤x-1成立.
若n为奇数,则难以判断g′(x)的符号.需要另起炉灶,考虑放缩:
要证f(x)≤x-1,由于<0,所以只需证ln(x-1)≤x-1;
可令h(x)=x-1-ln(x-1),则h′(x)=1-=≥0(x≥2),所以当x∈[2,+∞)时,h(x)=x-1-ln(x-1)单调递增;又h(2)=1>0,所以当x≥2时,恒有h(x)>0,即ln(x-1).
解析:(1)∵f(x)=ln x,g(x)=f(x+1)-x,
∴g(x)=ln(x+1)-x(x>-1),
∴g′(x)=-1.
令g′(x)=0,得x=0,
当-1<x<0时,g′(x)>0,
当x>0时,g′(x)<0,
又g(0)=0,
∴当且仅当x=0时,g(x)取得最大值0.
(2)证明:法一:分析所证不等式的结构,稍作变形:
f(b)-f(a)=ln ,=,
令x=,构造函数F(x)=ln x-(x>1),可得F(x)在区间(1,+∞)上递增,有F(x)>F(1)=0,得证.
法二:观察所证不等式的结构特征,联想几何意义可作如下变形:
待证不等式⇔>.
又<=,故只要证明>=f′(b)即可;
设P(a,f(a)),Q(b,f(b)),由于f(x)=ln x为上凸函数,可得割线PQ的斜率大于在点Q处的切线斜率,即kPQ=>=f′(b),得证.
点评 有些问题可变形为与x2-x1,有关的问题,可作换元t=x2-x1,t=
,将问题转化为关于一个变量t的问题,然后构造函数g(t)来解决问题.
[对点训练]
已知函数f(x)=ln x-a(x-1),a∈R,x∈[1,+∞),且f(x)≤恒成立,求a的取值范围.
解析:法一:含参直接构造
f(x)-=,
构造函数g(x)=xln x-a(x2-1),(x≥1),g′(x)=ln x+1-2ax,
令F(x)=g′(x)=ln x+1-2ax,F′(x)=.
①若a≤0,F′(x)>0,g′(x)在[1,+∞)上单调递增,g′(x)≥g′(1)=1-2a>0,
∴g(x)在[1,+∞)上单调递增,g(x)≥g(1)=0,从而f(x)-≥0,不符合题意.
②若00,∴g′(x)在上单调递增,从而g′(x)>g′(1)=1-2a,以下论证同①一样,所以不符合题意.
③若a≥,F′(x)≤0在[1,+∞)上恒成立,
∴g′(x)在[1,+∞)上单调递减,g′(x)≤g′(1)=1-2a≤0.
从而g(x)≤g(1)=0,f(x)-≤0,
综上所述,a的取值范围是.
法二:巧妙两边构造
当x≥1时,f(x)≤恒成立等价于ln x-≤a(x-1),
不等式两边分别构造函数:h(x)=ln x-=,g(x)=a(x-1).
h′(x)=,∵x≥1,∴h′(x)>0,即h(x)在[1,+∞)上是增函数.
g′(x)=a,∵当a>0时,g(x)在[1,+∞)上是增函数,
又∵h(1)=g(1)=0,∴要使h(x)≤g(x)(x≥1)恒成立,只需h′(1)≤g′(1),
易解得a∈.
授课提示:对应学生用书第121页
1.(2018·胶州模拟)已知函数f(x)=(a∈R,e为自然对数的底数,e≈2.718 28).
(1)若曲线y=f(x)在x=0处的切线的斜率为-1,求实数a的值;
(2)求f(x)在[-1,1]上的最大值g(a);
(3)当a=0时,若对任意的x∈(0,1),恒有f(x)>f,求正实数m的最小值.
解析:(1)f′(x)==,f′(0)=1-a=-1,解得a=2.
(2)由f′(x)>0,得x<1-a;由f′(x)<0,得x>1-a.
所以f(x)的单调递增区间是(-∞,1-a),单调递减区间是(1-a,+∞).
当1-a<-1,即a>2时,f(x)在[-1,1]上单调递减,f(x)max=f(-1)=(a-1)e;
当-1≤1-a≤1,即0≤a≤2时,x=1-a为f(x)在区间[-1,1]上的极大值点,也是最大值点,所以f(x)max=f(1-a)=;
当1-a>1,即a<0时,f(x)在[-1,1]上单调递增,f(x)max=f(1)=.
所以g(a)=.
(3)当a=0时,由(2)知,f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减.
若0f(1),与f(x)在(-∞,1)上单调递增矛盾,所以只有m≥1.
当m≥1时,≥>1,所以f≥f,故只需f(x)>f,即可满足f(x)>f.
下面证明f(x)>f在区间(0,1)上恒成立.
f(x)>f,即>,即xe>ex,即x2>ex-,两边取对数,
得ln x>.
构造函数h(x)=ln x-,则h′(x)=-=,对任意的x∈(0,1),h′(x)<0,故h(x)在(0,1)上单调递减,
所以h(x)>h(1)=0,所以ln x>.
综上可知,正实数m的最小值为1.
2.(2018·贵阳模拟)设函数f(x)=xln(ax)(a>0).
(1)设F(x)=f(1)x2+f′(x),讨论函数F(x)的单调性;
(2)过两点A(x1,f′(x1)),B(x2,f′(x2))(x10,函数F(x)在(0,+∞)上是增函数;
②当ln a<0,即00,得(ln a)x2+1>0,解得0 .
所以函数F(x)在上为增函数,在上为减函数.
(2)证明:因为k===,x2-x1>0,要证1,则只要证1-0(t>1),故g(t)在(1,+∞)上是增函数.
所以当t>1时,g(t)=t-1-ln t>g(1)=0,即t-1>ln t成立.
②要证1-1,即证t-10(t>1),故函数h(t)在(1,+∞)上是增函数,
所以当t>1时,h(t)=tln t-(t-1)>h(1)=0,即 t-1k(x-1)+ax-x恒成立,求正整数k的值.
解析:(1)由f(x)=xln x+ax,得f′(x)=ln x+a+1,
∵函数f(x)在区间[e2,+∞)上为增函数,
∴当x∈[e2,+∞)时,f′(x)≥0,
即ln x+a+1≥0在区间[e2,+∞)上恒成立,
∴a≥-1-ln x.
又当x∈[e2,+∞) 时,ln x∈[2,+∞),∴-1-ln x∈(-∞,-3].
∴a≥-3.
(2)若对任意x∈(1,+∞),f(x)>k(x-1)+ax-x恒成立,
即xln x+ax>k(x-1)+ax-x恒成立,
也就是k(x-1)0.
则问题转化为k<对任意x∈(1,+∞)恒成立.
设函数h(x)=,则h′(x)=,
再设m(x)=x-ln x-2,则m′(x)=1-.
∵x∈(1,+∞),∴m′(x)>0,
则m(x)=x-ln x-2在(1,+∞)上为增函数 ,
∵m(1)=1-ln 1-2=-1,m(2)=2-ln 2-2=-ln 2,
m(3)=3-ln 3-2=1-ln 3<0,m(4)=4-ln 4-2=2-ln 4>0.
∴∃x0∈(3,4),使m(x0)=x0-ln x0-2=0.
∴当x∈(1,x0)时,m(x)<0,h′(x)<0,
∴h(x)=在(1,x0)上单调递减,
当x∈(x0,+∞)时,m(x)>0,h′(x)>0,
∴h(x)=在(x0,+∞)上单调递增,
∴h(x)的最小值为h(x0)=.
∵m(x0)=x0-ln x0-2=0,∴ln x0+1=x0-1,代入函数h(x)=得h(x0)=x0,
∵x0∈(3,4),且k成立.
解析:由题意得f′(x)=+2ax-(2a+1)==,x∈(0,+∞).
(1)由题意得f′(2)=1,即=1,解得a=.
(2)①当a≤0时,2ax-1<0在(0,+∞)上恒成立,由f′(x)>0得01,故函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
②当a>0时,令f′(x)=0得x=1或x=,
当<1,即a>时,由f′(x)>0得x>1或01,即00,得x>或0时,函数f(x)在上单调递增,在上单调递减,在(1,+∞)上单调递增.
(3)证明:由(2)知,当a=1时,函数f(x)=ln x+x2-3x在(1,+∞)上单调递增,∴ln x+x2-3x≥f(1)=-2,即ln x≥-x2+3x-2=-(x-1)(x-2),
令x=1+,n∈N*,则ln>-,
∴ln+ln+ln+…+ln>-+-+-+…+-,
∴ln>-+-+-+…+-,即ln(1+n)>
.
故对任意的n∈N*,都有ln(1+n)> 成立.