2012年烟台中考数学试卷

2012年烟台中考数学试卷

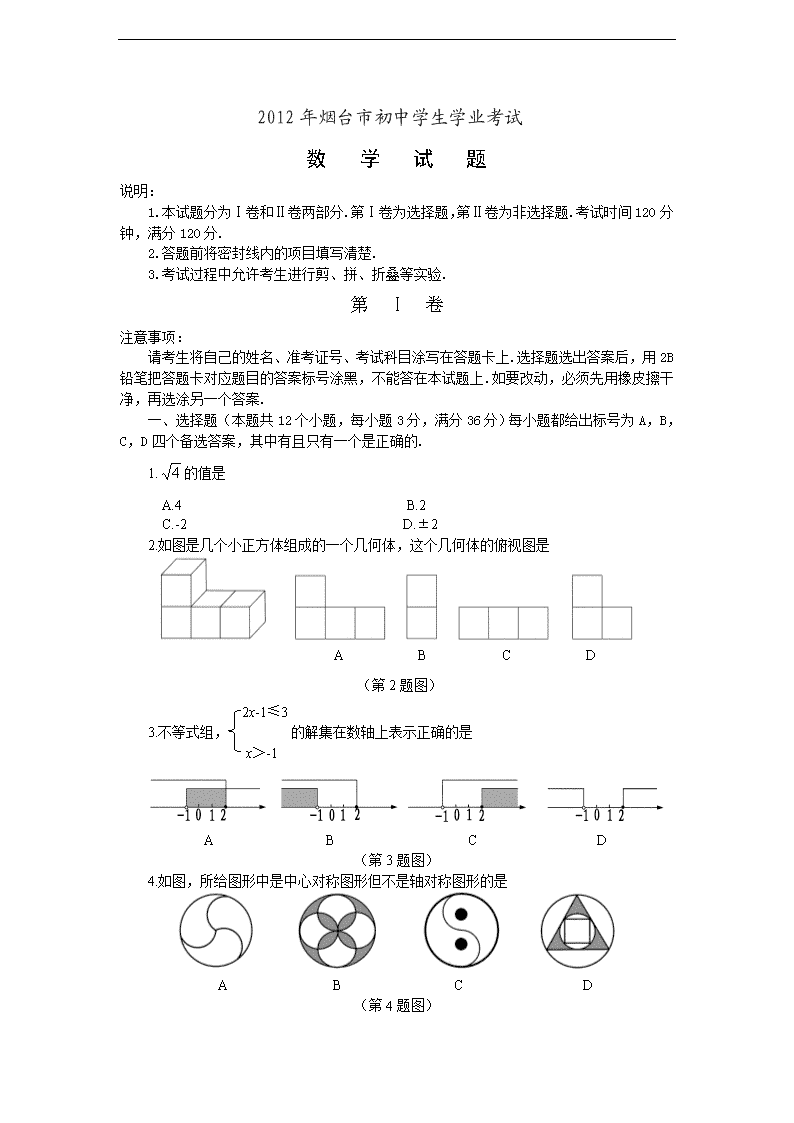
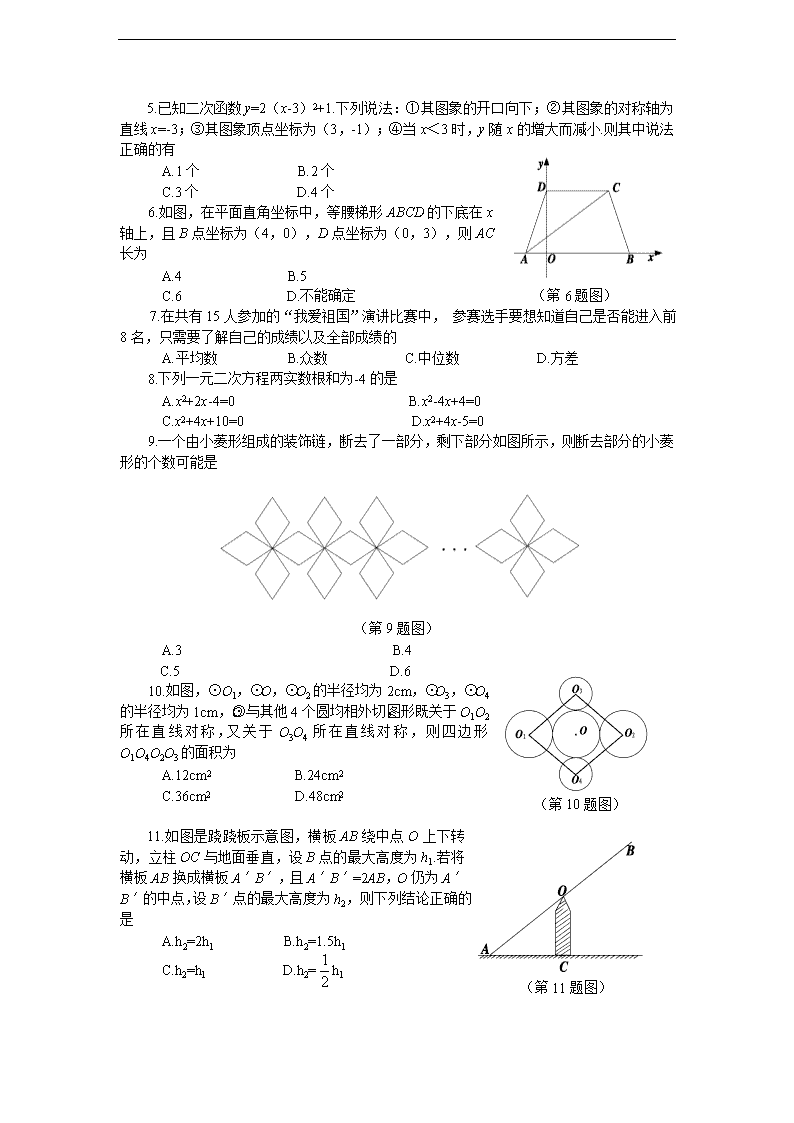
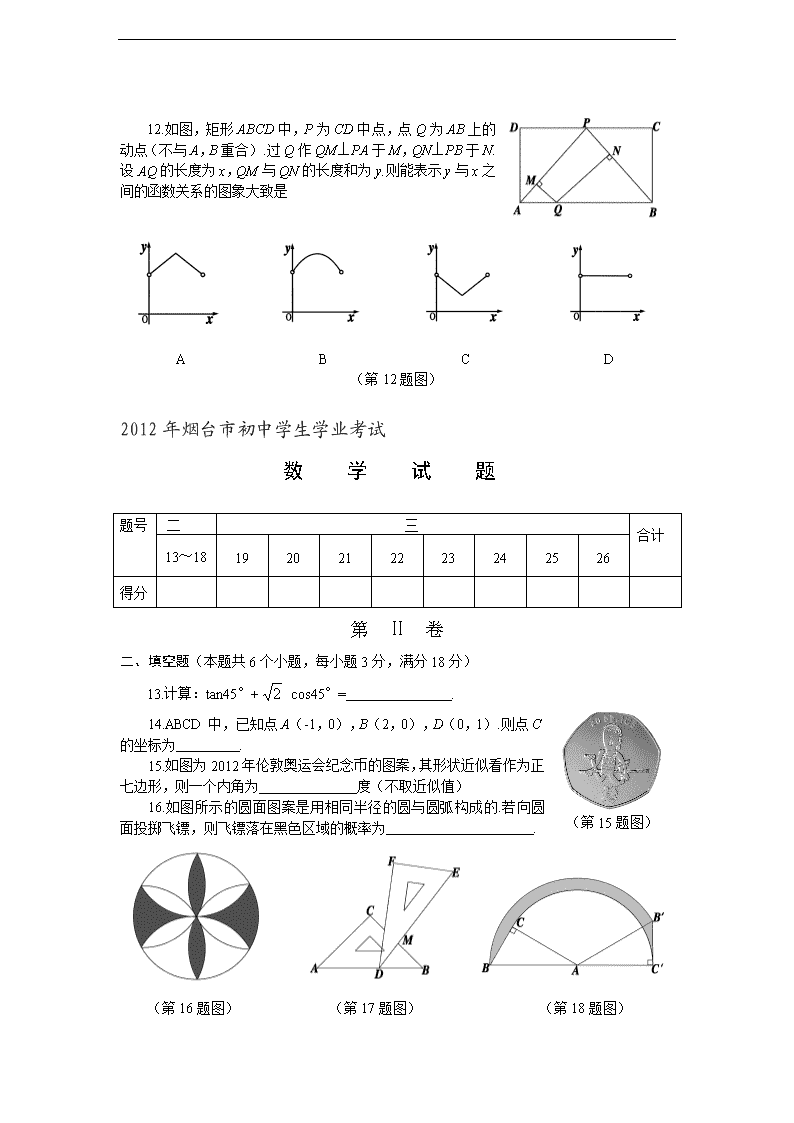
‎2012年烟台市初中学生学业考试 数 学 试 题 说明：‎ ‎1.本试题分为Ⅰ卷和Ⅱ卷两部分.第Ⅰ卷为选择题，第Ⅱ卷为非选择题.考试时间120分钟，满分120分.‎ ‎2.答题前将密封线内的项目填写清楚.‎ ‎3.考试过程中允许考生进行剪、拼、折叠等实验.‎ 第 Ⅰ 卷 注意事项：‎ 请考生将自己的姓名、准考证号、考试科目涂写在答题卡上.选择题选出答案后，用2B铅笔把答题卡对应题目的答案标号涂黑，不能答在本试题上.如要改动，必须先用橡皮擦干净，再选涂另一个答案.‎ 一、选择题（本题共12个小题，每小题3分，满分36分）每小题都给出标号为A，B，C，D四个备选答案，其中有且只有一个是正确的.‎ ‎1.的值是 A.4 B.2‎ C.-2 D.±2 ‎2.如图是几个小正方体组成的一个几何体，这个几何体的俯视图是 A B C D ‎（第2题图）‎ ‎2x-1≤3‎ ‎3.不等式组， 的解集在数轴上表示正确的是 x＞-1‎ A B C D ‎（第3题图）‎ ‎4.如图，所给图形中是中心对称图形但不是轴对称图形的是 A B C D ‎（第4题图）‎ ‎5.已知二次函数y=2（x-3）2+1.下列说法：①其图象的开口向下；②其图象的对称轴为直线x=-3；③其图象顶点坐标为（3，-1）；④当x＜3时，y随x的增大而减小.则其中说法正确的有 A.1个 B.2个 C.3个 D.4个 ‎6.如图，在平面直角坐标中，等腰梯形ABCD的下底在x轴上，且B点坐标为（4，0），D点坐标为（0，3），则AC长为 A.4 B.5‎ C.6 D.不能确定 （第6题图）‎ ‎7.在共有15人参加的“我爱祖国”演讲比赛中， 参赛选手要想知道自己是否能进入前8名，只需要了解自己的成绩以及全部成绩的 A.平均数 B.众数 C.中位数 D.方差 ‎8.下列一元二次方程两实数根和为-4的是 A.x2+2x-4=0 B.x2-4x+4=0‎ C.x2+4x+10=0 D.x2+4x-5=0‎ ‎9.一个由小菱形组成的装饰链，断去了一部分，剩下部分如图所示，则断去部分的小菱形的个数可能是 ‎（第9题图）‎ A.3 B.4 ‎ ‎（第10题图）‎ C.5 D.6‎ ‎10.如图，⊙O1，⊙O，⊙O2的半径均为2cm，⊙O3，⊙O4的半径均为1cm，⊙O与其他4个圆均相外切，图形既关于O1O2所在直线对称，又关于O3O4所在直线对称，则四边形O1O4O2O3的面积为 A.12cm2 B.24cm2‎ C.36cm2 D.48cm2‎ ‎（‎ ‎（第11题图）‎ ‎11.如图是跷跷板示意图，横板AB绕中点O上下转动，立柱OC与地面垂直，设B点的最大高度为h1.若将横板AB换成横板A′B′，且A′B′=2AB，O仍为A′B′的中点，设B′点的最大高度为h2，则下列结论正确的是 A.h2=2h1 B.h2=1.5h1‎ C.h2=h1 D.h2=h1 ‎ ‎12.如图，矩形ABCD中，P为CD中点，点Q为AB上的动点（不与A，B重合）.过Q作QM⊥PA于M，QN⊥PB于N.设AQ的长度为x，QM与QN的长度和为y.则能表示y与x之间的函数关系的图象大致是 A B C D ‎（第12题图）‎ ‎2012年烟台市初中学生学业考试 数 学 试 题 题号21世纪教育网21世纪教育网 二[来源:21世纪教育网]‎ 三21世纪教育网 合计21世纪教育网 ‎13～18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ ‎26‎ 得分 第 Ⅱ 卷 二、填空题（本题共6个小题，每小题3分，满分18分）‎ ‎（第15题图）‎ ‎13.计算：tan45°+ cos45°= .‎ ‎14.ABCD中，已知点A（-1，0），B（2，0），D（0，1）.则点C的坐标为 . ‎ ‎15.如图为2012年伦敦奥运会纪念币的图案，其形状近似看作为正七边形，则一个内角为 度（不取近似值） ‎ ‎16.如图所示的圆面图案是用相同半径的圆与圆弧构成的.若向圆面投掷飞镖，则飞镖落在黑色区域的概率为 .‎ ‎ ‎ ‎（第16题图） （第17题图） （第18题图）‎ ‎17.一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M.如果∠ADF=100°，那么∠BMD为 度.‎ ‎18.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2.将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置，B，A，C′三点共线，则线段BC扫过的区域面积为 .‎ 三、解答题（本大题共8个小题，满分66分）‎ ‎19.（本题满分5分）‎ 化简：‎ ‎20.（本题满分6分）‎ 第三届亚洲沙滩运动会服务中心要在某校选拔一名志愿者.经笔试、面试，结果小明和小颖并列第一.评委会决定通过抓球来确定人选.抓球规则如下：在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球，小明先取出一个球，记住颜色后放回，然后小颖再取出一个球.若取出的球都是红球，则小明胜出；若取出的球是一红一绿，则小颖胜出.你认为这个规则对双方公平吗？请用列表法或画树状图的方法进行分析.‎ ‎21.（本题满分8分）‎ 某市为了鼓励居民节约用电，采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时，按0.55元/度计费；月用电量超过200度时，其中的200度仍按0.55元/度计费，超过部分按0.70元/度计费.设每户家庭月用电量为x度时，应交电费y元.‎ ‎（1）分别求出0≤x≤200和x＞200时，y与x的函数表达式；‎ ‎（2）小明家5月份交纳电费117元，小明家这个月用电多少度？‎ ‎22.（本题满分9分）‎ 某市园林处去年植树节在滨海路两侧栽了A，B，C三个品种的树苗.栽种的A，B，C三个品种树苗数量的扇形统计图如图（1），其中B种树苗数量对应的扇形圆心角为120°.今年植树节前管理员调查了这三个品种树苗的成活率情况，准备今年从三个品种中选成活率最高的品种再进行栽种.经调查得知： A品种的成活率为85%，三个品种的总成活率为89%，但三个品种树苗成活数量统计图尚不完整，如图（2）.‎ 请你根据以上信息帮管理员解决下列问题：‎ ‎（1）三个品种树苗去年共栽多少棵？‎ ‎（2）补全条形统计图，并通过计算，说明今年应栽哪个品种的树苗.‎ ‎ ‎ 图（1） 图（2）‎ ‎（第22题图）‎ ‎23.（本题满分8分）‎ 如图，在平面直角坐标系中，A，B两点的纵坐标分别为7和1，直线AB与y轴所夹锐角为60°.‎ ‎（1）求线段AB的长；‎ ‎（2）求经过A，B两点的反比例函数的解析式.‎ ‎（第23题图）‎ ‎24.（本题满分8分）‎ 如图，AB为⊙O的直径，弦CD⊥AB，垂足为点E，CF⊥AF，且CF=CE.‎ ‎（1）求证：CF是⊙O的切线；‎ ‎（2）若sin∠BAC=2/5，求的值.‎ ‎（第24题图）‎ ‎25.（本题满分10分）‎ ‎（1）问题探究 如图1，分别以△ABC的边AC与边BC为边，向△ABC外作正方形ACD1E1和正方形BCD2E2，过点C作直线KH交直线AB于点H，使∠AHK=∠ACD1作D1M⊥KH，D2N⊥KH，垂足分别为点M，N.试探究线段D1M与线段D2N的数量关系，并加以证明.‎ ‎（2）拓展延伸 ‎①如图2，若将“问题探究”中的正方形改为正三角形，过点C作直线K1H1，K2H2，分别交直线AB于点H1，H2，使∠AH1K1=∠BH2K2=∠ACD1.作D1M⊥K1H1，D2N⊥K2H2，垂足分别为点M，N.D1M=D2N是否仍成立？若成立，给出证明；若不成立，说明理由.‎ ‎②如图3，若将①中的“正三角形”改为“正五边形”，其他条件不变.D1M=D2N是否仍成立？（要求：在图3中补全图形，注明字母，直接写出结论，不需证明）‎ 图1 图2 图3 ‎（第25题图）‎ ‎26.（本题满分12分）‎ 如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）.以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发，沿线段AB向点B运动.同时动点Q从点C出发，沿线段CD向点D运动.点P，Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.‎ ‎（1）直接写出点A的坐标，并求出抛物线的解析式；‎ ‎（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？‎ ‎（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值.‎ ‎（第26题图）‎ ‎2012年烟台市初中学生学业考试 数学试题参考答案及评分意见 本试题答案及评分意见，供阅卷评分使用.考生若写出其它正确答案，可参照评分意见相应评分.‎ 一、选择题（本题共12个小题，每小题3分，满分36分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C A C A B C D C B C D 二、填空题（本题共6个小题，每小题3分，满分18分）‎ ‎13. 2 14.（3，1） 15. 16. 17. 85 18. ‎ 三、解答题(本题共8个小题，满分66分)‎ ‎19.（本题满分5分） 解：原式=………………………………2分 ‎= ……………………………………………4分 ‎= …………………………………………………………5分 ‎20.（本题满分6分） 解：根据题意，列出树状图如下： ‎ ‎ 第20题图……………………………………3分 由此可知，共有9种等可能的结果，其中，两红球及一红一绿各有4种结果 P（都是红球）=…………………………………………………………………4分 P（1红1绿球）=………………………………………………………………5分 因此，这个规则对双方是公平的.…………………………………………………6分 ‎21.（本题满分8分） 解：（1）当0≤x≤200时，y与x的函数表达式是y=0.55x；……………………2分 当x＞200时，y与x的函数表达式是 y=0.55×200+0.7（x-200）， …………………………………………………………4分 即y=0.7x-30.……………………………………………………………………………5分 ‎（2）因为小明家5月份的电费超过110元，……6分 所以把y=117代入y=0.7x-30中，得x=210.…………………………………………7分 答：小明家5月份用电210度.[ZK]][JY。]8分 ‎22.（本题满分9分）‎ 解：（1）A品种树苗棵数为1020÷85%=1200.（棵）…1分 所以，三个品种树苗共栽棵数为1200÷40%=3000（棵）.…3分 ‎（2）B品种树苗成活棵数为 ‎3000×89%-1020-720=930（棵）.……………………5分 补全条形统计图，如图.………………………………7分 B品种树苗成活率为=93%；‎ C品种树苗成活率为=90%.‎ 所以，B品种成活率最高，今年应栽B品种树苗.……………9分 ‎23.（本题满分8分）‎ 解：（1）分别过点A，B作AC⊥x轴，‎ BD⊥AC，垂足分别为点C，D……………………1分 由题意，知∠BAC=60°， AD=7-1=6‎ ‎∴AB= ==12…………………………3分 ‎（2）设过A，B两点的反比例函数解析式为y=，A点坐标为（m，7）……4分 ‎∵BD=AD·tan60°=6，‎ ‎∴B点坐标为（m+6，1）………………………………………………5分 ‎ ‎7m=k，‎ ‎∴ ………………………………………………6分 ‎（m+6）·1=k.‎ 解得k=7…………………………………………………………………7分 ‎∴所求反比例函数的解析式为y=……………………………………8分 ‎24.（本题满分8分） 解：（1）证明：连接OC.………………………………1分 ‎∵CE⊥AB，CF⊥AF，CE=CF，‎ ‎∴AC平分∠BAF，即∠BAF=2∠BAC.………………2分 ‎∵∠BOC=2∠BAC，‎ ‎∴∠BOC=∠BAF.‎ ‎∴OC∥AF.‎ ‎∴CF⊥OC.………………………………………………3分 ‎∴CF是⊙O的切线.……………………………………4分 ‎ ‎（2）∵AB是⊙O的直径，CD⊥AB， ‎ ‎∴CE=ED.………………………………………………………………………………5分 ‎∴S△CBD=2S△CEB，∠BAC=∠BCE ‎∴△ABC∽△CBE.……………………………………………………………………6分 ‎∴S△CBE/S△ABC==（sin∠BAC）2==.………………………………7分 ‎∴S△CBD/S△ABC=.……………………………………………………………………8分 ‎25.（本题满分10分）‎ 解：（1）D1M=D2N.……………………………………………………………………1分 证明：∵∠ACD1=90°，‎ ‎∴∠ACH+∠D1CK=90°‎ ‎∵∠AHK=∠ACD1=90°，‎ ‎∴∠ACH+∠HAC=90°‎ ‎∴∠D1CK=∠HAC………………………………………………………………………2分 ‎∵AC=CD1，‎ ‎∴△ACH≌△CD1M ‎∴D1M=CH.………………………………………………………………………………3分 同理可证D2N=CH ‎∴D1M=D2N.……………………………………………………………………………4分 ‎（2）①证明：D1M=D2N成立.………………………………………………………5分 过点C作CG⊥AB，垂足为点G.‎ ‎∵∠H1AC+∠ACH1+∠AH1C=180°，‎ ‎∠D1CM+∠ACH1+∠ACD1=180°，‎ ‎∠AH1C=∠ACD1，‎ ‎∴∠H1AC=∠D1CM.……………………………………………………………………6分 ‎∵AC=CD1，∠AGC=∠CMD1=90°，‎ ‎∴△ACG≌△CD1M.‎ ‎∴CG=D1M.………………………………………………………………………………7分 同理可证CG=D2N.‎ ‎∴D1M=D2N.……………………………………………………………………………8分 ‎②作图正确.……………………………………………………………………………9分 D1M=D2N还成立.……………………………………………………………………10分 图1 图2 图3‎ ‎26.（本题满分12分）‎ 解：（1）A（1，4）.…………………………1分 由题意知，可设抛物线解析式为y=a(x-1) 2+4‎ 因抛物线过点C（3，0），‎ ‎∴0=a（3-1）2+4‎ ‎∴a=-1‎ 所以抛物线的解析式为y=-(x-1) 2+4，‎ 即y=-x2+2x+3.………………………………………… 2分 ‎（2）∵A（1，4），C（3，0）， ‎ ‎∴可求直线AC的解析式为y=-2x+6. ‎ 点P（1，4-t）.………………………………………………………………………3分 将y=4-t代入y=-2x+6中，解得点E的横坐标为x=1+.…………………………4分 ‎∴点G的横坐标为1+t/2，代入抛物线的解析式中，可求点G的纵坐标为4-t2/4.‎ ‎∴GE=（4-）-（4-t）=t-.………………………………………………………5分 又点A到GE的距离为t/2，C到GE的距离为2-t/2，‎ 即S△ACG=S△AEG+S△CEG=1/2·EG·t/2+1/2·EG（2-t/2）‎ ‎=·2（t-）=-（t-2）2+1.………………………………………7分 当t=2时，S△ACG的最大值为1.………………………………………………………8分 ‎（3）t=或t=20-8.………………………………………………12分 ‎（说明：每值各占2分，多出的值未舍去，每个扣1分）‎