- 2021-04-29 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版9年级上册数学全册导学案23_2_3《旋转》第二节中心对称导学案3
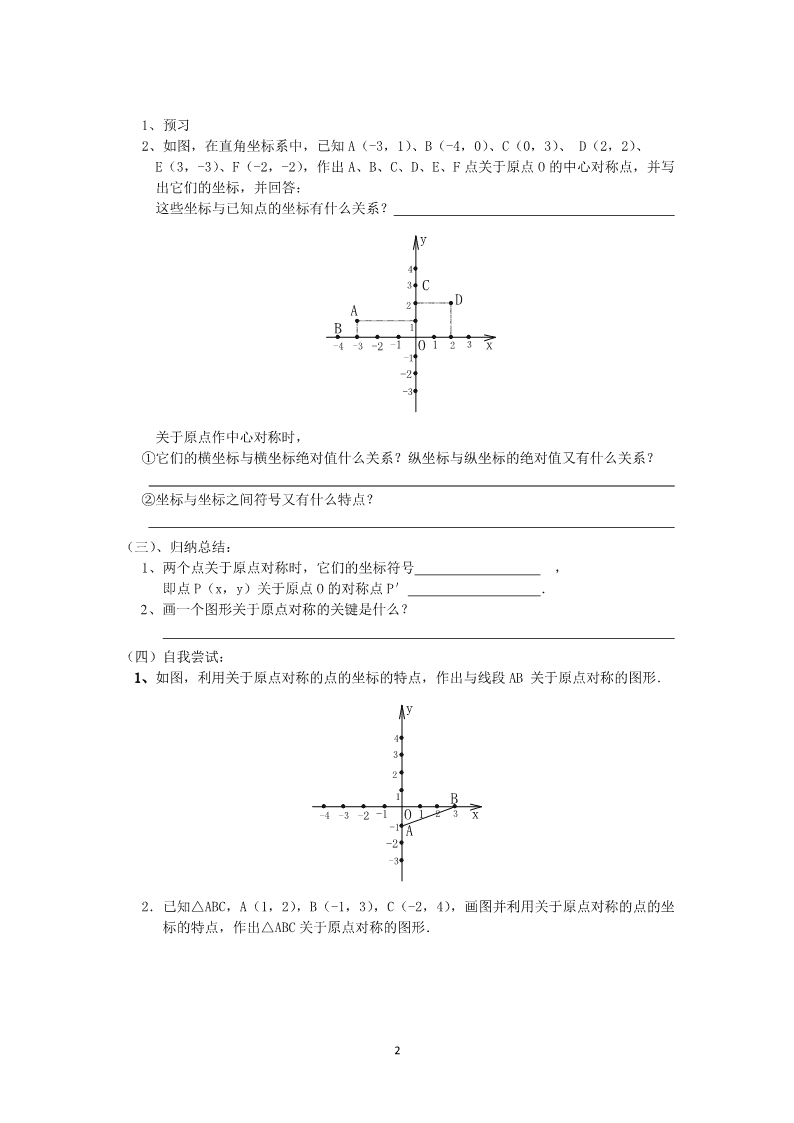
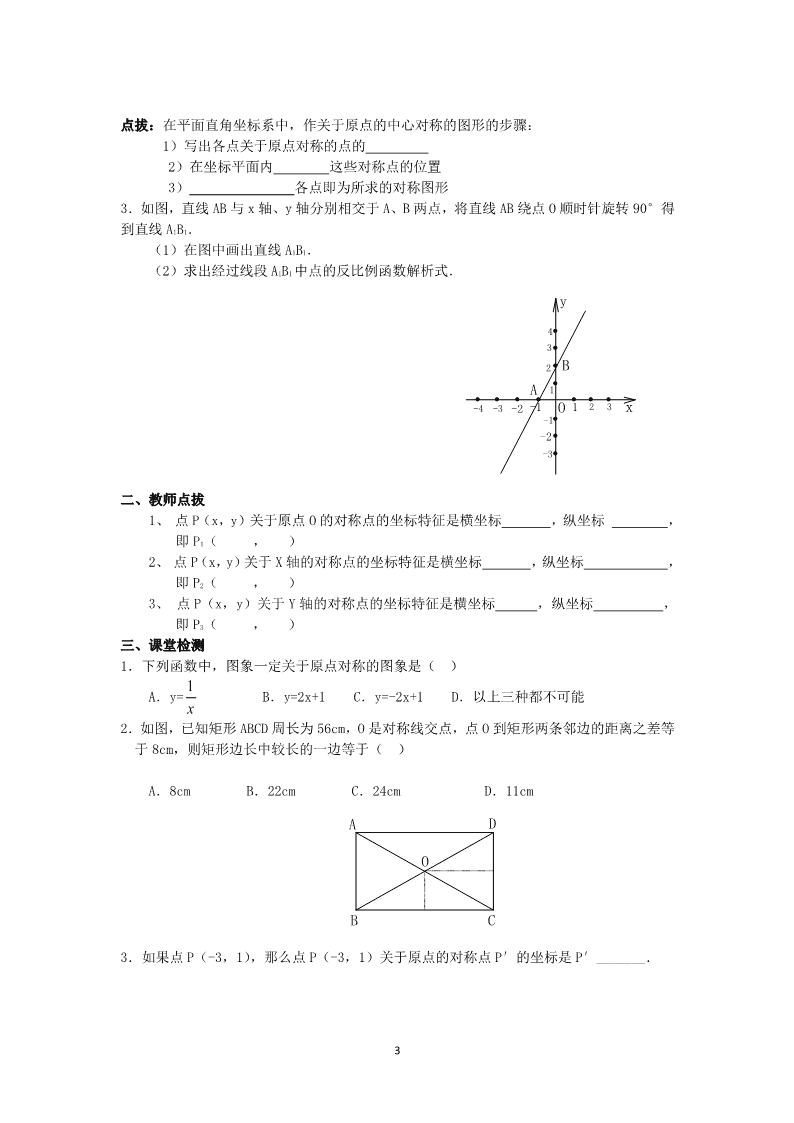
1 《旋转》第二节 中心对称导学案 3 主编人: 主审人: 班级: 学号: 姓名: 学习目标: 【知识与技能】 掌握在直角坐标系中关于原点对称的点的坐标的关系 【过程与方法】 经历操作——猜想——验证的实践过程,积累数学活动的经验 【情感、态度与价值观】 从坐标角度揭示中心对称与轴对称的关系,培养观察、分析、探究及合作交流的学习习惯,体验事物 的变化之间是有联系的 【重点】 关于原点对称的点的坐标的关系及初步应用. 【难点】 运用中心对称的知识导出关于原点对称的点的坐标的性质及其运用它解决实际问题 学习过程: 一、自主学习 (一)复习巩固 1.已知点 A 和直线 L,如图,请画出点 A 关于 L 对称的点 A′. l A 2.如图,△ABC 是正三角形,以点 A 为中心,把△ADC 顺时针旋转 60°,画出旋转后 的图形. 3.如图△ABO,绕点 O 旋转 180°,画出旋转后的图形. (二)自主探究 B A C 2 1、预习 2、如图,在直角坐标系中,已知 A(-3,1)、 B(-4,0)、 C(0,3)、 •D(2,2)、 E(3,-3)、 F(-2,-2),作出 A、B、C、D、E、F 点关于原点 O 的中心对称点,并写 出它们的坐标,并回答: 这些坐标与已知点的坐标有什么关系? -3 -3 3 O B A C -2 -2 1-1 y x3-4 D 4 2 2 1 -1 关于原点作中心对称时, •①它们的横坐标与横坐标绝对值什么关系?纵坐标与纵坐标的绝对值又有什么关系? ②坐标与坐标之间符号又有什么特点? (三)、归纳总结: 1、两个点关于原点对称时,它们的坐标符号 , 即点 P(x,y)关于原点 O 的对称点 P′ . 2、画一个图形关于原点对称的关键是什么? (四)自我尝试: 1、如图,利用关于原点对称的点的坐标的特点,作出与线段 AB•关于原点对称的图形. -3 -3 3 O B A -2 -2 1-1 y x3-4 4 2 2 1 -1 2.已知△ABC,A(1,2), B(-1,3), C(-2,4),画图并利用关于原点对称的点的坐 标的特点,作出△ABC 关于原点对称的图形. 3 点拔:在平面直角坐标系中,作关于原点的中心对称的图形的步骤: 1)写出各点关于原点对称的点的 2)在坐标平面内 这些对称点的位置 3) 各点即为所求的对称图形 3.如图,直线 AB 与 x 轴、y 轴分别相交于 A、B 两点,将直线 AB 绕点 O 顺时针旋转 90°得 到直线 A1B1. (1)在图中画出直线 A1B1. (2)求出经过线段 A1B1 中点的反比例函数解析式. -3 -3 3 O B A -2 -2 1-1 y x3-4 4 2 2 1 -1 二、教师点拔 1、 点 P(x,y)关于原点 O 的对称点的坐标特征是横坐标 ,纵坐标 , 即 P1( , ) 2、 点 P(x,y)关于 X 轴的对称点的坐标特征是横坐标 ,纵坐标 , 即 P2( , ) 3、 点 P(x,y)关于 Y 轴的对称点的坐标特征是横坐标 ,纵坐标 , 即 P3( , ) 三、课堂检测 1.下列函数中,图象一定关于原点对称的图象是( ) A.y= 1 x B.y=2x+1 C.y=-2x+1 D.以上三种都不可能 2.如图,已知矩形 ABCD 周长为 56cm,O 是对称线交点,点 O 到矩形两条邻边的距离之差等 于 8cm,则矩形边长中较长的一边等于( ) A.8cm B.22cm C.24cm D.11cm O B A C D 3.如果点 P(-3,1),那么点 P(-3,1)关于原点的对称点 P′的坐标是 P′_______. 4 4.写出函数 y=- 3 x 与 y= 具有的一个共同性质________(用对称的观点写). 四、课外拓展 1、如图,在平面直角坐标系中,A(-3,1), B(-2,3), C(0,2),画出△ABC•关于 x 轴 对称的△A′B′C′,再画出△A′B′C′关于 y 轴对称的△A″B″C″,那么△A″B″C″ 与△ABC 有什么关系,请说明理由. -3 -3 3B A C -2 -2 1-1 y x3-4 4 2 2 1 -1 O 2、过菱形对角线交点的一条直线,把菱形分成了两个梯形,这两个梯形是全等的吗? 3、如图,有一块长方形钢板,工人师傅想把它分成面积相等的两部分,请你用三种方法在 图中画出作图痕迹.查看更多