第十三章轴对称13-1轴对称13-1-2线段的垂直平分线的性质第1课时线段的垂直平分线的性质和判定作业课件新版 人教版

第十三章轴对称13-1轴对称13-1-2线段的垂直平分线的性质第1课时线段的垂直平分线的性质和判定作业课件新版 人教版

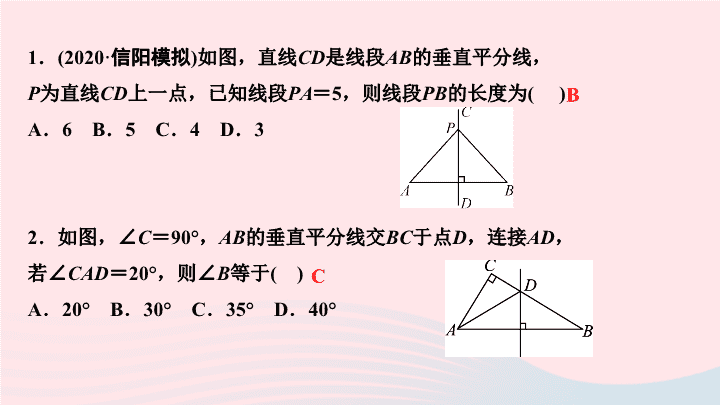
第十三章　轴对称 13．1　轴对称 13.1.2　线段的垂直平分线的性质 第 1 课时　线段的垂直平分线的性质和判定 1 ． (2020 · 信阳模拟 ) 如图，直线 CD 是线段 AB 的垂直平分线， P 为直线 CD 上一点，已知线段 PA ＝ 5 ，则线段 PB 的长度为 ( ) A ． 6 B ． 5 C ． 4 D ． 3 2 ．如图，∠ C ＝ 90° ， AB 的垂直平分线交 BC 于点 D ，连接 AD ， 若∠ CAD ＝ 20° ，则∠ B 等于 ( ) A ． 20° B ． 30° C ． 35° D ． 40° B C 3 ． ( 教材 P65 习题 6 变式 ) 如图，△ ABC 的周长为 30 cm ， 把△ ABC 的边 AC 对折，使顶点 C 和点 A 重合，折痕交 BC 边于点 D ， 交 AC 边于点 E ，若△ ABD 的周长是 22 cm ，则 AE 的长为 ( ) A ． 2 cm B ． 3 cm C ． 4 cm D ． 5 cm C 4 ． ( 毕节中考 ) 如图，在△ ABC 中， AC ＝ 10 ， BC ＝ 6 ， AB 的垂直平分线交 AB 于点 D ，交 AC 于点 E ，则△ BCE 的周长是 ____ ． 16 5 ．如图， AD ⊥ BC ， BD ＝ CD ，点 C 在 AE 的垂直平分线上． 若 AB ＝ 5 cm ， BD ＝ 3 cm ，求 BE 的长． 解：∵ BD ＝ CD ，∴ BC ＝ 2 BD ＝ 6 cm ，又∵ AD ⊥ BC ， ∴由 SAS 可证△ ABD ≌△ ACD ，∴ AB ＝ AC ＝ 5 cm. ∵ 点 C 在 AE 的垂直平分线上，∴ CE ＝ AC ＝ 5 cm ， ∴ BE ＝ BC ＋ CE ＝ 11 cm 6 ．如图， AC ＝ AD ， BC ＝ BD ，则有 ( ) A. AB 垂直平分 CD B ． CD 垂直平分 AB C ． AB 与 CD 互相垂直平分 D ． CD 平分∠ ACB A 7 ．在锐角△ ABC 内有一点 P ，满足 PA ＝ PB ＝ PC ，则点 P 是△ ABC ( ) A ．三边垂直平分线的交点 B ．三条角平分线的交点 C ．三条高的交点 D ．三边中线的交点 A 8 ．如图，点 D 在 △ ABC 的 BC 边上，且 BC ＝ BD ＋ AD ， 则点 D 在 ____ 的垂直平分线上 . AC 9 ．如图， AB ＝ AC ， DB ＝ DC ， E 是 AD 延长线上的一点， 则 BE 是否与 CE 相等？试说明理由． 解： BE ＝ CE . 理由：连接 BC ， ∵ AB ＝ AC ， DB ＝ DC ， ∴ A ， D 都在线段 BC 的垂直平分线上，即 AD 垂直平分 BC ， ∴ BE ＝ CE 10 ．如图，已知钝角 △ ABC ，其中 ∠ A 是钝角，求作 AC 边上的高 BH . ( 尺规作图，保留作图痕迹，不写过程 ) 解： BH 即为所求，如图： 11 ．如图，在四边形 ABCD 中， AC 垂直平分 BD ，垂足为 E ， 下列结论不一定成立的是 ( ) A ． AB ＝ AD B ． CA 平分∠ BCD C ． AB ＝ BD D ．△ BEC ≌△ DEC C 12 ． ( 洛阳东方中学期末 ) 如图，∠ MON 内有一点 P ， PP 1 ， PP 2 分别 被 OM ， ON 垂直平分， P 1 P 2 与 OM ， ON 分别交于点 A ， B . 若 P 1 P 2 ＝ 10 cm ，则△ PAB 的周长为 ( ) A ． 6 cm B ． 8 cm C ． 10 cm D ． 12 cm C 13 ．如图， BD 垂直平分线段 AC ， AE ⊥ BC ，垂足为 E ，交 BD 于点 P ， PE ＝ 3 cm ，则点 P 到直线 AB 的距离是 ___cm. 3 14 ．如图，已知 AB 比 AC 长 2 cm ， BC 的垂直平分线交 AB 于点 D ， 交 BC 于点 E ，△ ACD 的周长是 14 cm ，求 AB 和 AC 的长． 解：∵ DE 垂直平分 BC ，∴ BD ＝ CD ， ∴△ ACD 的周长＝ AD ＋ AC ＋ CD ＝ AB ＋ AC ＝ 14 cm ， 又∵ AB － AC ＝ 2 cm ，可得 AB ＝ 8 cm ， AC ＝ 6 cm 15 ．如图，在 Rt△ ABC 中，∠ C ＝ 90° ， AB ＝ 2 AC ， AD 为∠ BAC 的平分线．求证：点 D 在线段 AB 的垂直平分线上． 解：过点 D 作 DE ⊥ AB 于点 E ，由 AAS 可证△ ACD ≌△ AED ， ∴ AC ＝ AE .∵ AB ＝ 2 AC ＝ BE ＋ AE ，∴ BE ＝ AE ＝ AC ， ∴ DE 是线段 AB 的垂直平分线，即点 D 在线段 AB 的垂直平分线上 16 ．如图，在△ ABC 中，∠ BAC 的平分线与 BC 的垂直平分线 PQ 相交于 点 P ，过点 P 分别作 PN ⊥ AB 于点 N ， PM ⊥ AC 于点 M . 求证： BN ＝ CM . 解：连接 PB ， PC ，由角的平分线的性质证 PN ＝ PM ， 由线段垂直平分线的性质证 PB ＝ PC ， 从而由 HL 证 Rt△ PNB ≌Rt△ PMC ，∴ BN ＝ CM 17 ．如图，在△ ABC 中，∠ B ＝∠ C ，点 D ， E ， F 分别在三边上， 且 BE ＝ CD ， BD ＝ CF ， G 为 EF 的中点．求证： DG 垂直平分 EF . 解：连接 DE ， DF ，由 SAS 证△ BED ≌△ CDF ，∴ DE ＝ DF ， 又∵ GE ＝ GF ， GD ＝ GD ，∴△ GED ≌△ GFD (SSS) ， ∴∠ EGD ＝∠ FGD ＝ 90° ，即 DG ⊥ EF ，∴ DG 垂直平分 EF