中考数学规律探索专题复习

中考数学规律探索专题复习

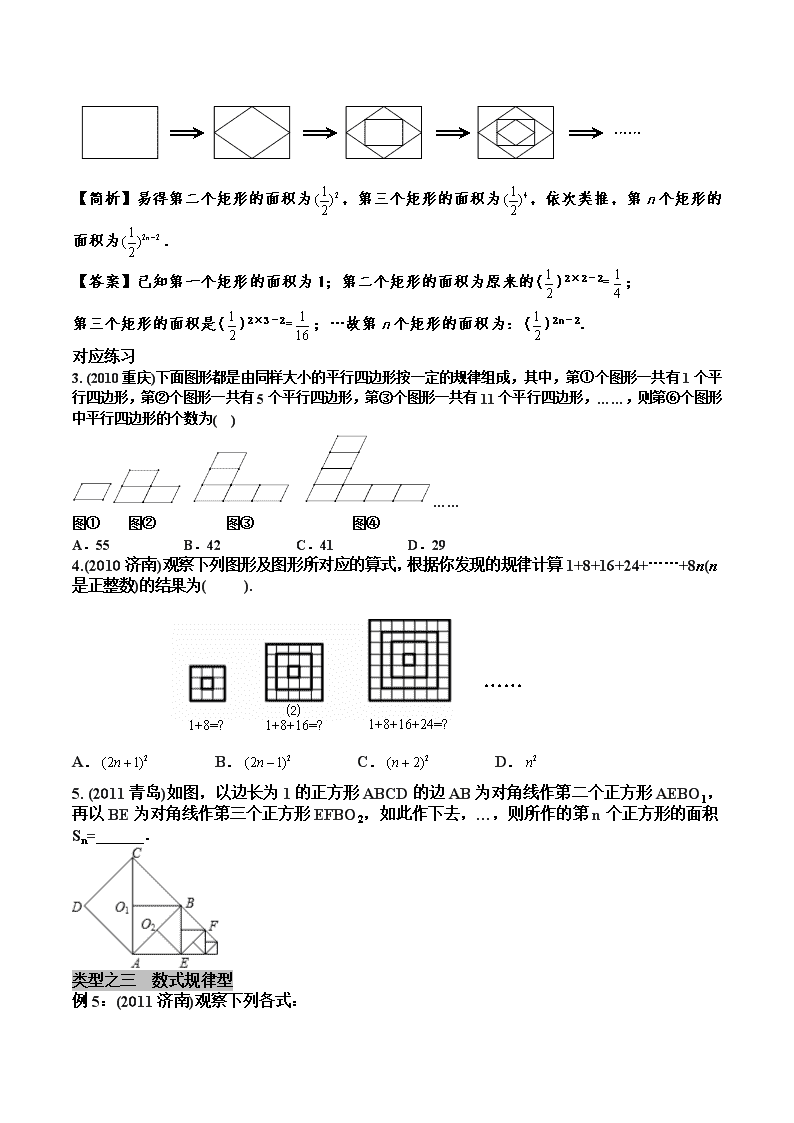
中考数学规律探索专题复习 ‎ 一、典例精析 类型之一　数字规律型 例1. (2011丽江)下面是按一定规律排列的一列数：，，，，…那么第n个数是 . ‎【简析】根据题意，首先从各个数开始分析，n=1时，分子：2=(﹣1)2•21，分母：3=2×1+1；n=2时，分子：﹣4=(﹣1)3•22，分母：5=2×2+1；…，即可推出第n个数为.‎ ‎【答案】解：∵n=1时，分子：2=(-1)2•21，分母：3=2×1+1；n=2时，分子：﹣4=(-1)3•22，分母：5=2×2+1；‎ n=3时，分子：8=(-1)4•23，分母：7=2×3+1；n=4时，分子：﹣16=(-1)5•24，分母：9=2×4+1；…，‎ ‎∴第n个数为： 故答案为：.‎ 例2：(2010深圳) 观察下列算式，用你所发现的规律得出22010的末位数字是(　　).‎ ‎21＝2,22＝4,23＝8,24＝16,25＝32,26＝64,27＝128,28＝256，…‎ A．2 B．‎4 C．6 D．8‎ ‎【简析】有些题目包含着事物的循环规律，找到了事物的循环规律，其他问题就可以迎刃而解.通过观察可以发现，本题中的数字从第1个到第4个为一个循环节，以此规律总结下来，第2010个图形应该就是一个循环节中的第2个数字，故选B.‎ ‎【答案】B 对应练习 ‎1.有一组数：1，2，5，10，17，26，……，请观察这组数的构成规律，用你发现的规律确定第8个数为　　　　　　　．‎ ‎2.(2011湛江)若：A32=3×2=6，A53=5×4×3=60，A54=5×4×3×2=120，A64=6×5×4×3=360，…，观察前面计算过程，寻找计算规律计算A73=　 　(直接写出计算结果)，并比较A‎103　‎ 　A104(填“＞”或“＜”或“=”)‎ 类型之二　图形规律型 例3：(2011•临沂)如图，上面各图都是用全等的等边三角形拼成的一组图形．则在第10个这样的图形中共有　 　个等腰梯形．‎ ‎【简析】本题考查了图形的变化，解题的关键是按照一定的顺序依次找到符合条件的等腰梯形，做到不重复不遗漏．由于图②4个=2+1+1，图③8个3+2+2+1+1，图④16=4+3+3+2+2+1+1，由此即可得到第10个图形中等腰梯形的个数为：‎ ‎10+9+9+8+8+7+7+6+6+5+5+4+4+3+3+2+2+1+1=100．‎ ‎【答案】100．‎ 例4： (2011兰州)如图，依次连结第一个矩形各边的中点得到一个菱形，再依次连结菱形各边的中点得到第二个矩形，按照此方法继续下去.已知第一个矩形的面积为1，则第n个矩形的面积为 .‎ ‎……‎ ‎【简析】易得第二个矩形的面积为，第三个矩形的面积为，依次类推，第n个矩形的面积为．‎ ‎【答案】已知第一个矩形的面积为1；第二个矩形的面积为原来的()2×2﹣2=；‎ 第三个矩形的面积是()2×3﹣2=；…故第n个矩形的面积为：()2n﹣2．‎ 对应练习 ‎3. (2010重庆)下面图形都是由同样大小的平行四边形按一定的规律组成，其中，第①个图形一共有1个平行四边形，第②个图形一共有5个平行四边形，第③个图形一共有11个平行四边形，……，则第⑥个图形中平行四边形的个数为( )‎ ‎……‎ 图① 图② 图③ 图④‎ A．55 B．‎42 ‎ C．41 D．29‎ ‎4.(2010济南)观察下列图形及图形所对应的算式，根据你发现的规律计算1+8+16+24+……+8n(n是正整数)的结果为( ).‎ ‎1+8=?‎ ‎1+8+16=?‎ ‎⑵‎ ‎1+8+16+24=?‎ ‎……‎ ‎⑶‎ ‎⑴‎ A． B． C． D．‎ ‎5. (2011青岛)如图，以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1，再以BE为对角线作第三个正方形EFBO2，如此作下去，…，则所作的第n个正方形的面积Sn= ．‎ 类型之三　数式规律型 例5：(2011济南)观察下列各式：‎ ‎(1)1=12；(2)2+3+4=32；(3)3+4+5+6+7=52；(4)4+5+6+7+8+9+10=72…‎ 请你根据观察得到的规律判断下列各式正确的是( )‎ A．1005+1006+1007+…+3016=20112 B．1005+1006+1007+…+3017=20112‎ C．1006+1007+1008+…+3016=20112 D．1007+1008+1009+…+3017=20112‎ ‎【简析】根据已知条件找出数字规律a+(a+1)+(a+2)+…+(a+n)=(a+n﹣a+1)2，依次判断各个式子即可得出结果．‎ ‎【解答】根据(1)1=12；(2)2+3+4=32；(3)3+4+5+6+7=52；(4)4+5+6+7+8+9+10=77‎ 可得出：a+(a+1)+(a+2)+…+(a+n)=(a+n﹣a+1)2，‎ 依次判断各选项，只有C符合要求，故选C．‎ 例6：(2011成都)设,,,…, ‎ 设，则S＝_________ (用含n的代数式表示，其中n为正整数)．‎ ‎【简析】，求，得出一般规律．‎ ‎∵，‎ ‎∴，‎ ‎∴‎ ‎【答案】‎ 对应练习 ‎6(2011常德)先找规律，再填数：，，，，‎ 则- =．‎ ‎7(2009济南)在平面直角坐标系中，对于平面内任一点若规定以下三种变换：‎ 按照以上变换有：那么等于( )‎ A． B． C． D．‎ 类型之四 坐标规律型 例7：(2011•莱芜)如图①，在△AOB中，∠AOB=90°，OA=3，OB=4．将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转，分别得到图②、图③、…，则旋转得到的图⑩的直角顶点的坐标为　_________　．‎ ‎【简析】有些题目包含着事物的循环规律，找到了事物的循环规律，其他问题就可以迎刃而解.本题主要考查了旋转的性质、坐标与图形的性质及勾股定理，找出图形旋转的规律“旋转3次为一循环”，是解答本题的关键．如图，在△AOB中，∠AOB=90°，OA=3，OB=4，则AB=5，每旋转3次为一循环，则图③、④的直角顶点坐标为(12，0)，图⑥、⑦的直角顶点坐标为(24，0)，所以，图⑨、⑩10的直角顶点为(36，0)．‎ ‎【解答】∵在△AOB中，∠AOB=90°，OA=3，OB=4，∴AB=5，‎ ‎∴图③、④的直角顶点坐标为(12，0)，‎ ‎∵每旋转3次为一循环，∴图⑥、⑦的直角顶点坐标为(24，0)，‎ ‎∴图⑨、⑩的直角顶点为(36，0)．‎ ‎【答案】(36，0)．‎ 例8(2011盐城)将1、、、按右侧方式排列．若规定(m，n)表示第m排从左向右第n个数，则(5，4)与(15，7)表示的两数之积是　 ．‎ ‎【简析】：根据数的排列方法可知，第一排：1个数，第二排2个数．第三排3个数，第四排4个数，…第m－1排有(m－1)个数，从第一排到(m－1)排共有：1+2+3+4+…+(m－1)个数，根据数的排列方法，每四个数一个轮回，根据题目意思找出第m排第n个数到底是哪个数后再计算．‎ ‎ (5，4)表示第5排从左向右第4个数是：，(15，7)表示第15排从左向右第7个数是：，＝2．‎ ‎【答案】2．‎ 对应练习 ‎8. (2011•贺州)如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，…，按这样的运动规律，经过第2011次运动后，动点P的坐标是　 ．‎ ‎9. (2011梧州)如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称或中心对称变换，若原来点A坐标是(a，b)，则经过第2011次变换后所得的A点坐标是　 　．‎ 类型之五 图表规律 例9：(2011•遵义)有一数值转换器，原理如图所示，若开始输入x的值是5，可发现第一次输出的结果是8，第二次输出的结果是4，…，请你探索第2011次输出的结果是　 　．‎ ‎【简析】首先由数值转换器，发现第二次输出的结果是4 为偶数，所以第三次输出的结果为2，第四次为1，第五次为4，第六次为2，…，可得出规律从第二次开始每三次一个循环，根据此规律求出第2011次输出的结果．‎ ‎【答案】由已知要求得出：第一次输出结果为8，第二次为4，则第三次为2，第四次为1，‎ 那么第五次为4，…，所以得到从第二次开始每三次一个循环，(2011﹣1)÷3=670，‎ 所以第2011次输出的结果是1．‎ ‎【答案】1．‎ 例10：(2010广东)如下数表是由从1开始的连续自然数组成，观察规律并完成各题的解答．‎ ‎1‎ ‎2 3 4‎ ‎5 6 7 8 9‎ ‎10 11 12 13 14 15 16‎ ‎17 18 19 20 21 22 23 24 25‎ ‎26 27 28 29 30 31 32 33 34 35 36‎ ‎ …………………………‎ ‎(1)表中第8行的最后一个数是______________，它是自然数_____________的平方，第8行共有____________个数；‎ ‎(2)用含n的代数式表示：第n行的第一个数是___________________，最后一个数是 ‎________________，第n行共有_______________个数；‎ ‎(3)求第n行各数之和．‎ ‎【简析】(1)数为自然数，每行数的个数为1，3，5，…的奇数列，很容易得到所求之数；(2)知第n行最后一数为n2，则第一个数为n2﹣2n+2，每行数由题意知每行数的个数为1，3，5，…的奇数列，故个数为2n﹣1；(3)通过以上两部列公式从而解得．‎ ‎【解答】 (1)每行数的个数为1，3，5，…的奇数列，由题意最后一个数是该行数的平方即得64，‎ 其他也随之解得：8，15；‎ ‎(2)由(1)知第n行最后一数为n2，则第一个数为n2﹣2n+2，‎ 每行数由题意知每行数的个数为1，3，5，…的奇数列，‎ 故个数为2n﹣1；‎ ‎(3)第n行各数之和：×(2n﹣1)=(n2﹣n+1)(2n﹣1)．‎ 对应练习：‎ ‎10. (2011綦江)如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2011个格子中的数为(　　)‎ ‎3‎ a b c ‎－1‎ ‎2‎ ‎…‎ ‎ A．3 B．‎2 ‎ C．0 D．－1‎ 类型之六 与函数有关的规律型 例11：在直角坐标系中，正方形A1B‎1C1O1、A2B‎2C2C1、…、AnBnCnCn-1按如图所示的方式放置，其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上，点C1、C2、C3、…、Cn均在x轴上．若点B1的坐标为(1，1)，点B2的坐标为(3，2)，则点An的坐标为 ．‎ ‎【简析】首先求得直线的解析式，分别求得A1，A2，A3…的坐标，可以得到一定的规律，据此即可求解．‎ ‎【解答】解：A1的坐标是(0，1)，A2的坐标是：(1，2)， 根据题意得：，解得：．则直线的解析式是：y=x+1． ∵A1B1=1，点B2的坐标为(3，2)，∴A1的纵坐标是1，A2的纵坐标是2． 在直线y=x+1中，令x=3，则纵坐标是：3+1=4=22；则A4的横坐标是：1+2+4=7，则A4的纵坐标是：7+1=8=23；据此可以得到An的纵坐标是：2n-1，横坐标是：2n-1-1．故点An的坐标为 (2n-1-1，2n-1)．‎ ‎【答案】(2n-1-1，2n-1)．‎ 例12： (2011广安)如图4所示，直线OP经过点P(4, )，过x轴上的点l、3、5、7、9、‎ ‎11……分别作x轴的垂线，与直线OP相交得到一组梯形，其阴影部分梯形的面积从左至右依次记为S1、S2、S3……Sn，则Sn关于n的函数关系式是____________．‎ ‎【简析】运用待定系数法可以确定一次函数的解析式，根据函数解析式，已知自变量的值可求得函数的值，从而可以确定每个梯形的上底与下底的长，根据梯形的面积公式可计算出每个梯形的面积，由此发现规律，根据规律可得Sn关于n的函数关系式．‎ 设直线OP的函数解析式为，根据题意可知，所以．所以．当时，；当时，；当时，；当时，；当时，；当时，；…；所以，，，…，‎ 所以．‎ ‎【答案】‎ 对应练习：‎ ‎11.(2011威海)如图，在直线l1⊥x轴于点(1，0)，直线l2⊥x轴于点(2，0)，直线l3⊥x轴于点(3，0)…直线ln⊥x轴于点(n，0)．函数y=x的图象与直线l1，l2，l3，…ln分别交于点A1，A2，A3，…An，函数y=2x的图象与直线l1，l2，l3，…ln分别交于点B1，B2，B3，…Bn．如果△OA1B1的面积记为S1，四边形A‎1A2B2B1的面积记作S2，四边形A‎2A3B3B2的面积记作S3，…四边形An–1AnBnBn–1的面积记作Sn，那么S2011= ．‎ 达标演练 ‎1.(2011•日照)观察图中正方形四个顶点所标的数字规律，可知数2011应标在(　　)‎ ‎ A.第502个正方形的左下角 B.第502个正方形的右下角 ‎ C.第503个正方形的左上角 D.第503个正方形的右下角 ‎2.(2011济宁)如图，观察每一个图中黑色正六边形的排列规律，则第10个图中黑色正六边形有　 个．‎ ‎3.(2011•南平)观察下列各图形中小正方形的个数，依此规律，第(11)个图形中小正方形的个数为(　　) ‎ ‎ A．78 B. ‎66 ‎ C. 55 D. 50‎ ‎4.(2011东营)如图，观察由棱长为1的小立方体摆成的图形，寻找规律：如图①中：共有1个小立方体，其中1个看得见，0个看不见；如图②中：共有8个小立方体，其中7个看得见，1个看不见；如图③中：共有27个小立方体，其中19个看得见，8个看不见；…，则第⑥个图中，看得见的小立方体有　　个．‎ ‎5. (2011烟台) 如图，六边形ABCDEF是正六边形，曲线FK1K2K3K4K5K6K7……叫做“正六边形的渐开线”，其中弧FK1，弧K1 K2，弧K2 K3，弧K3 K4，弧K4K5，弧K5 K6，……的圆心依次按点A，B，C，D，E，F循环，其弧长分别记为l1，l2，l3，l4，l5，l6，…….当AB＝1时，l2 011等于( )‎ A. B. C. D. ‎ ‎6.(2011•安顺)一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到(0，1)，然后接着按图中箭头所示方向跳动[即(0，0)→(0，1)→(1，1)→(1，0)→…]，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是(　　)‎ ‎ A、(4，O) B、(5，0) C、(0，5) D、(5，5)‎ ‎7.将正整数按如图所示的规律排列下去.若用有序实数对(n，m)表示第n排，从左到右第m个数，如(4，3)表示实数9，则(7，2)表示的实数是 .‎ ‎8. (2011菏泽)填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值是　 　．‎