- 2021-04-28 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届数学(理)二轮复习第2部分专题2解密高考② 数列问题重在“归”——化归、归纳学案
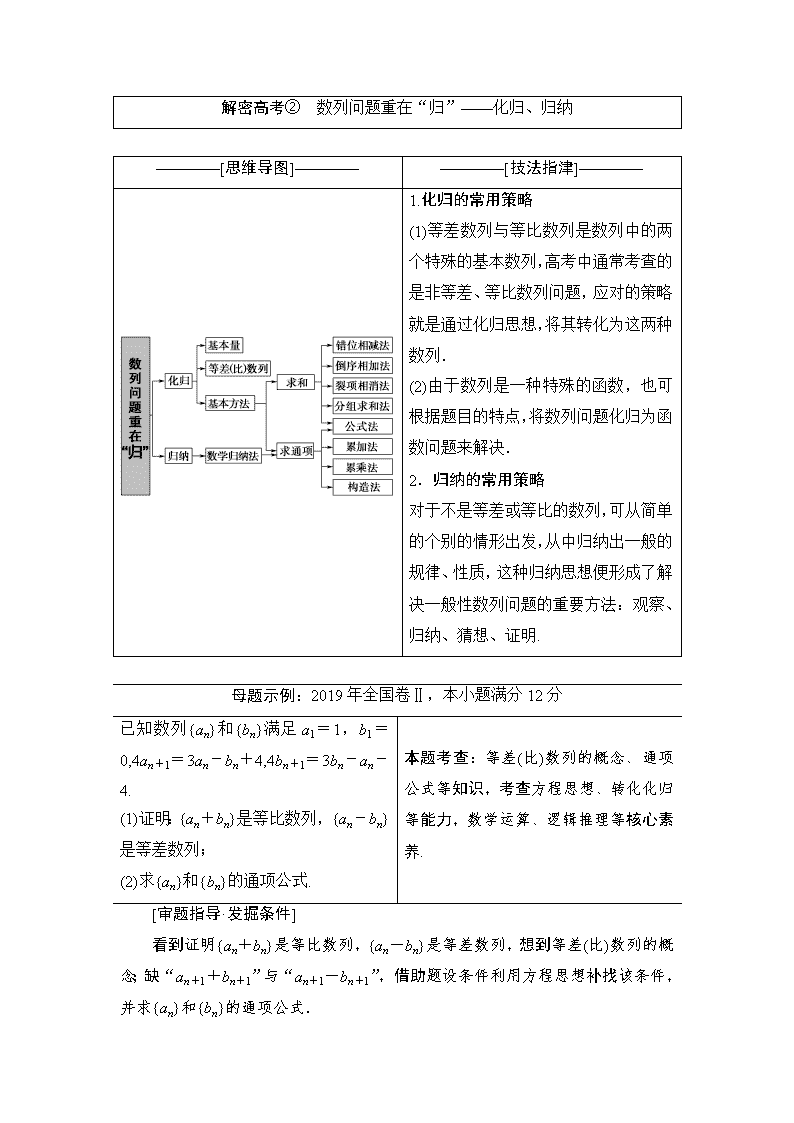
解密高考② 数列问题重在“归”——化归、归纳 ————[思维导图]———— ————[技法指津]———— 1.化归的常用策略 (1)等差数列与等比数列是数列中的两个特殊的基本数列,高考中通常考查的是非等差、等比数列问题,应对的策略就是通过化归思想,将其转化为这两种数列. (2)由于数列是一种特殊的函数,也可根据题目的特点,将数列问题化归为函数问题来解决. 2.归纳的常用策略 对于不是等差或等比的数列,可从简单的个别的情形出发,从中归纳出一般的规律、性质,这种归纳思想便形成了解决一般性数列问题的重要方法:观察、归纳、猜想、证明. 母题示例:2019年全国卷Ⅱ,本小题满分12分 已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an-bn+4,4bn+1=3bn-an-4. (1)证明:{an+bn}是等比数列,{an-bn}是等差数列; (2)求{an}和{bn}的通项公式. 本题考查:等差(比)数列的概念、通项公式等知识,考查方程思想、转化化归等能力,数学运算、逻辑推理等核心素养. [审题指导·发掘条件] 看到证明{an+bn}是等比数列,{an-bn}是等差数列,想到等差(比)数列的概念;缺“an+1+bn+1”与“an+1-bn+1”,借助题设条件利用方程思想补找该条件,并求{an}和{bn}的通项公式. [构建模板·四步解法] 数列类问题的求解策略 第一步 找条件 第二步 求通项 第三步 定方法 第四步 再反思 根据已知条件确定数列的项之间的关系 根据等差或等比数列的通项公式,求数列的通项公式 根据题设条件及数列表达式的结构特征,选择合适的方法,求解相应问题 审视转化过程的等价性与合理性 母题突破:2019年潍坊二模,本小题满分12分 已知数列{an}满足a1=2,(n+2)an=(n+1)an+1-2(n2+3n+2),设bn=. (1)证明数列{bn}是等差数列; (2)设=2n+1,求数列{cn}的前n项和Tn(n∈N*). [解](1)因为a1=2,所以b1==1. 1分 将(n+2)an=(n+1)an+1-2(n2+3n+2)两边同时除以(n+1)(n+2)得:=-2, 3分 ∴-=2,即bn+1-bn=2. 4分 ∴数列{bn}是以1为首项,2为公差的等差数列. 5分 (2)由(1)得bn=1+2(n-1)=2n-1. 6分 ∵ =2n+1,∴cn=(2n+1)bn=(2n-1)·2n+2n-1. 7分 设Pn=1×2+3×22+5×23+…+(2n-1)·2n, 2Pn=1×22+3×23+…+(2n-3)·2n+(2n-1)·2n+1, 8分 两式相减得:-Pn=2+2(22+23+…+2n )-(2n-1)·2n+1 =2+2×-(2n-1)·2n+1=-6-(2n-3)·2n+1.化简得Pn=6+(2n-3)·2n+1. 10分 设Sn=1+3+5+…+(2n-1)==n2, 11分 ∴Tn=Pn+Sn=6+(2n-3)·2n+1+n2. 12分查看更多