2014湖北省十堰市中考数学试卷

2014湖北省十堰市中考数学试卷

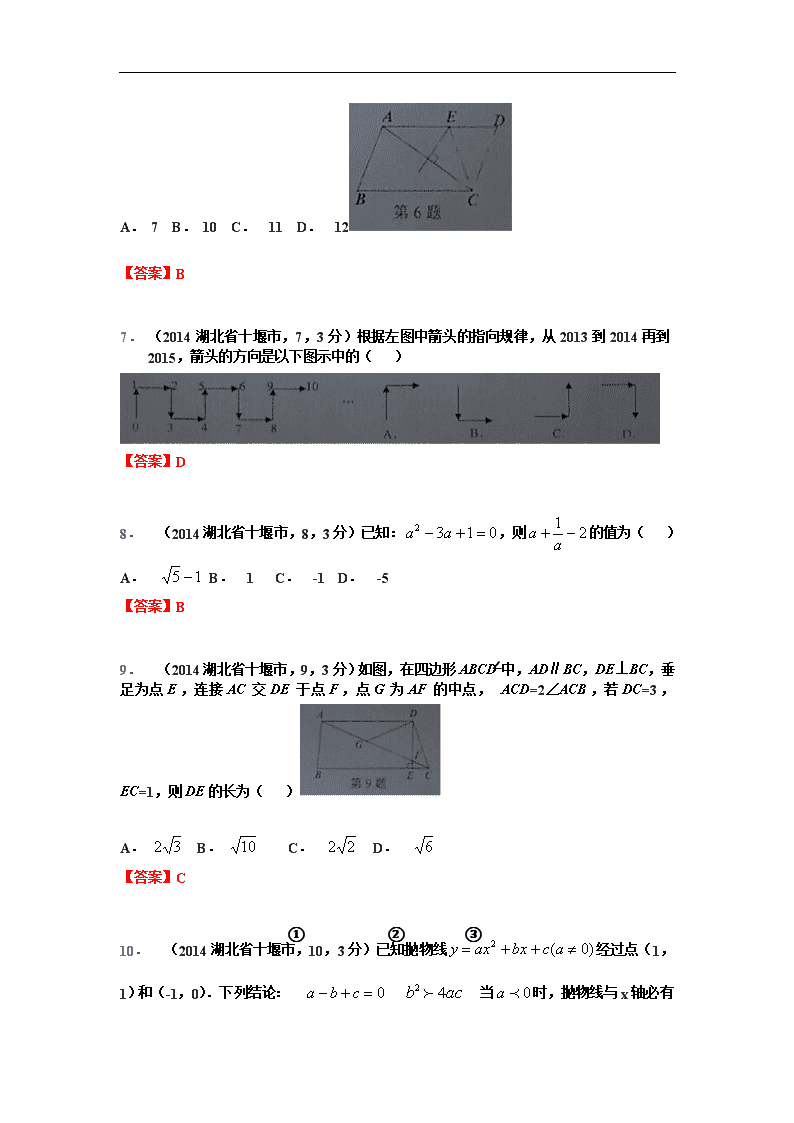
‎2014年湖北省十堰市中考数学试卷 ‎（满分120分，考试时间120分钟）‎ 一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1．（2014湖北省十堰市，1，3分）3的倒数是（ ）‎ A． B． C． D． ‎ ‎【答案】A ‎2． （2014湖北省十堰市，2，3分）如图，直线m∥n，则∠α为（ ）‎ A． 70° B． 65° C． 50° D． 40°‎ ‎【答案】C ‎3．（2014湖北省十堰市，3， 3分）在正南的四个几何体中，左视图与主视图不相同的几何体是（ ）‎ ‎【答案】B ‎4． （2014湖北省十堰市，4，3分）下列计算正确的是（ ）‎ A． B． C． D． ‎ ‎【答案】D ‎5． （2014湖北省十堰市，5，3分）为了调查某小区 居民的用水情况，随机抽查了若干户家庭的月用水量，结果如下表：‎ 月用水量（吨）‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ 户数 ‎2‎ ‎3‎ ‎4‎ ‎1‎ 则关于这若干户家庭的月用水量，下列说法错误的是（ ）‎ A．众数是4 B．平均数是4．‎6 C． 调查了10户家庭的月用水量D． 中位数是4．5‎ ‎【答案】A ‎6． （2014湖北省十堰市，6，3分）如图，在平行四边形ABCD中，AB=4，BC=6，AC的垂直平分线交AD与点B，则△CDE的周长是（ ）‎ A． 7 B． ‎10 C． 11 D． 12‎ ‎【答案】B ‎7． （2014湖北省十堰市，7，3分）根据左图中箭头的指向规律，从2013到2014再到2015，箭头的方向是以下图示中的（ ）‎ ‎【答案】D ‎8． jscm（2014湖北省十堰市，8，3分）已知：，则的值为（ ）‎ A． B． ‎1 C． -1 D． -5‎ ‎【答案】B ‎9． jscm（2014湖北省十堰市，9，3分）如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD=2∠ACB，若DC=3，EC=1，则DE的长为（ ）‎ A． B． C． D． ‎ ‎【答案】C ‎10． jscm（2014湖北省十堰市，10，3分）已知抛物线经过点（1，1）和（-1，0）．下列结论：①②③当时，抛物线与x 轴必有一个交点在点（1，0）的右侧；④抛物线的对称轴为，其中结论正确的个数有（ ）‎ A． 4个 B． 3个 C． 2个 D． 1个 ‎ ‎【答案】B 二、填空题（本大题共6小题，每小题3分，满分18分．）‎ ‎11．（2014湖北省十堰市，11，3分）世界文化遗产长城总长约‎6700000m，用科学记数法表示这个数为 m．‎ ‎【答案】6．7×106‎ ‎12． （2014湖北省十堰市，12，3分）计算： ‎ ‎【答案】1‎ ‎13． （2014湖北省十堰市，13，3分）不等式组的解集为 ‎ ‎【答案】‎ ‎14． （2014湖北省十堰市，14，3分）如图，在△ABC中，点D是BC的中点，点E、F分别在线段AD及其延长线上，且DE=DF，给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC；从中选择一个条件使四边形BECF是菱形，你认为这个条件是 （只填写序号）‎ ‎【答案】③‎ ‎15． （2014湖北省十堰市，15，3分）如图，轮船在A处观测灯塔C位于北偏西70°方向上，轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行，1小时后到达码头B处，此时，观测灯塔C位于北偏西25°方向上，则灯塔C与码头B的距离是 海里（结果精确到个位，参考数据：，，）‎ ‎【答案】24‎ ‎16． （2014湖北省十堰市，16，3分）如图，扇形OAB中，∠AOB=60°，扇形半径为4，点C在弧AB上，CD⊥OA，垂足为点D，当△OCD的面积最大时，图中阴影部分的面积为 ．‎ ‎【答案】‎ ‎17． jscm（2014湖北省十堰市，17，3分）‎ ‎【答案】‎ ‎18．jscm（2014湖北省十堰市，18，3分）‎ ‎【答案】‎ ‎19． （2014湖北省十堰市，19，3分）‎ ‎【答案】‎ ‎20． （2014湖北省十堰市，20，3分）‎ ‎【答案】‎ 三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤）‎ ‎21．（2014湖北省十堰市，21，分）‎ ‎【答案】解：‎ ‎22． jscm（2014湖北省十堰市，22，分）‎ ‎【答案】解：‎ ‎23． （2014湖北省十堰市，23，8分）如图，点B(3,3)在双曲线上，点D在双曲线上，点A和点C分别在x轴，y轴的正半轴上，且点A,B,C,D构成的四边形为正方形．（1）求k值；（2）求点A的坐标．‎ ‎【答案】解：（1）∵点B(3,3)在反比例上∴k=3×3=9‎ ‎（2）分别作DM⊥x轴，BN⊥x轴， ‎ ‎∵ A,B,C,D构成的四边形为正方形 ‎∴ DA=AB，∠DAB=90°‎ ‎∵ ∠DMA=∠ANB= 90°，∠ADM=∠BAN ‎∴ △ADM≌△BAN ‎∴ DM=AN，MA=BN 设OA=x，则DM=MO=3-x ‎∵点D在双曲线上 ‎∴(3-x)2=4，解得x=1，‎ ‎∴点A的坐标（1，0）‎ ‎24． （2014湖北省十堰市，24，10分）如图1，AB为半圆的直径，O为圆心，C为圆弧上一点，AD垂直于过点C的切线，垂足为D，AB的延长线交直线CD于点E．（1）求证：AC平分∠DAB；（2）若AB=4，B为OE的中点，CF⊥AB，垂足为点F，求CF的长；（3）如图2，连接OD交AC于点G，若，求sin∠E的值． ‎ ‎【答案】解：（1）连接OC，‎ ‎∵CD是切线 ‎∴OC⊥DC ‎∵AD⊥DC ‎∴OC∥AD ‎∴∠DAC=∠CAF ‎∵OC=OA ‎∴∠OCF=∠OAF ‎∴∠OAF=∠DAF ‎∴AC平分∠DAB；‎ ‎（2）∵∠OCB=90，OC=OB=BE ‎∴∠COF=60‎ ‎∵OC=2，CF⊥AB ‎∴CF=‎ ‎（3）∵OC∥AD ‎ ‎∴,‎ 设CO=3k，则AD=4k，AO=3k，OE=9k ‎∴sin∠E=‎ ‎25． （2014湖北省十堰市，25，12分）已知抛物线C1：的顶点为A，且经过点B(-2,-1)．‎ ‎(1)求A点的坐标和抛物线C1的解析式；‎ ‎(2)如图1，将抛物线C1向下平移2个单位后得到抛物线C2，且抛物线C2与直线AB相交于C、D两点，求S△OAC:S△OAD的值；‎ ‎(3)如图2，若过P（-4，0），Q（0，2）的直线为l，点E在（2）中抛物线C2对称轴右侧部分（含顶点）运动，直线m过点C和点E，问：是否存在直线m，使得直线l，m与x轴围成的三角形和直线l，m与y轴围成的三角形相似？若存在，求出直线m的解析式；若不存在，说明理由．‎ ‎【答案】解：（1）∵抛物线C1：经过点B(-2，-1)．‎ ‎∴ a=1‎ ‎∴, 顶点A点的坐标（-1，-2），‎ ‎（2）抛物线向下平移2个单位 抛物线C2: ‎ ‎∵ A（-1，-2），B(-2，-1)．‎ ‎∴ 直线AB解析式为 ‎∴ 解得，‎ ‎∴ C（-3，0），D（0，-3）‎ ‎∵ A（-1，-2），B(-2，-1)．‎ ‎∴ CB=BA=AD ‎∵ S△OAC:S△OAD=2：1‎ ‎（3）存在，直线m的解析式为：，与直线l交于点M，与y轴交于点N。‎ ‎∴PC=1，CO=3，PO=4，QO=2。‎ M N M N 如图1，当MN⊥PQ时，△QMN～△CMP，此时△CON～△QOP ‎∴ ∴ON=6‎ ‎∵C（-3，0），N(0，-6)．‎ ‎∴直线CN解析式为 如图2，当∴∠MPC=∠MNQ时，△QMN～△CMP，此时△CON～△QOP ‎∴ ∴ON=6‎ ‎∵C（-3，0），N(0，-6)．‎ ‎∴直线CN解析式为 综上，存在满足题意的直线m，解析式为或．‎