- 2021-04-28 发布 |
- 37.5 KB |
- 50页
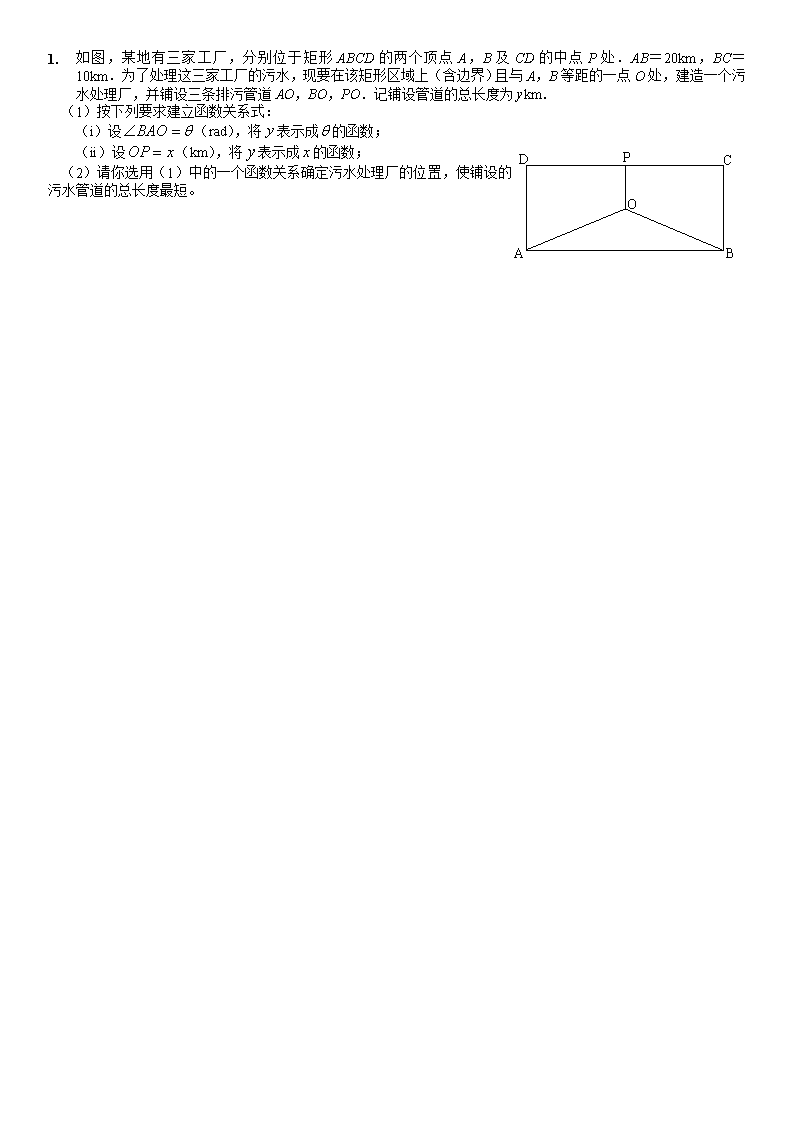


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江苏高考 应用题专项题
1. 如图,某地有三家工厂,分别位于矩形ABCD的两个顶点A,B及CD的中点P处.AB=20km,BC=10km.为了处理这三家工厂的污水,现要在该矩形区域上(含边界)且与A,B等距的一点O处,建造一个污水处理厂,并铺设三条排污管道AO,BO,PO.记铺设管道的总长度为ykm. (1)按下列要求建立函数关系式: B C D A O P (i)设(rad),将表示成的函数; (ii)设(km),将表示成的函数; (2)请你选用(1)中的一个函数关系确定污水处理厂的位置,使铺设的污水管道的总长度最短。 某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=,∠ADE=。 (1) 该小组已经测得一组、的值,tan=1.24,tan=1.20,请据此算出H的值; (2) 该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使与之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,-最大? 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm (1)若广告商要求包装盒侧面积S(cm)最大,试问x应取何值? (2)若广告商要求包装盒容积V(cm)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。 P 某运输装置如图所示,其中钢结构是,的固定装置,AB上可滑动的点C使垂直于底面(不与重合),且可伸缩(当CD伸缩时,装置ABD随之绕D在同一平面内旋转),利用该运输装置可以将货物从地面处沿运送至处,货物从处至处运行速度为,从处至处运行速度为.为了使运送货物的时间最短,需在运送前调整运输装置中的大小. (1)当变化时,试将货物运行的时间表示成的函数(用含有和的式子); (2)当最小时,点应设计在的什么位置? 如图,实线部分DE,DF,EF是某风景区设计的游客观光路线平面图,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,.若游客在每条路线上游览的“留恋度”均与相应的线段或弧的长度成正比,且“留恋度”与路线DE,DF的长度的比例系数为2,与路线EF的长度的比例系数为1,假定该风景区整体的“留恋度”是游客游览所有路线“留恋度”的和. (I)试将表示为的函数; (II)试确定当取何值时,该风景区整体的“留恋度”最佳? 如图,海上有两个小岛相距10,船O将保持观望A岛和B岛所成的视角为,现从船O上派下一只小艇沿方向驶至处进行作业,且.设. (1)用分别表示和,并求出的取值范围; (2)晚上小艇在处发出一道强烈的光线照射A岛,B岛至光线的距离为,求BD的最大值. (第18题图) 如图,在海岸线一侧C处有一个美丽的小岛,某旅游公司为方便游客,在上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米。公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛。据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元。设∠,每批游客从各自报名点到C岛所需运输成本S元。 ⑴写出S关于的函数表达式,并指出的取值范围; ⑵问中转点D距离A处多远时,S最小? 如图所示,一科学考察船从港口出发,沿北偏东角的射线方向航行,而在离港口(为正常数)海里的北偏东角的A处有一个供给科考船物资的小岛,其中,.现指挥部需要紧急征调沿海岸线港口正东m()海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜. Z 东 北 A B C O ⑴ 求S关于m的函数关系式; ⑵ 应征调m为何值处的船只,补给最适宜. 如图,某兴趣小组测得菱形养殖区的固定投食点到两条平行河岸线的距离分别为 4m、8m,河岸线与该养殖区的最近点的距离为1m,与该养殖区的最近点的距离为2m. (1)如图甲,养殖区在投食点的右侧,若该小组测得,请据此算出养殖区的面积; (2)如图乙,养殖区在投食点的两侧,试在该小组未测得的大小的情况下,估算出养 (图甲) (图乙) 殖区的最小面积. D C 如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件ABCD,设梯形部件ABCD的面积为平方米. (I)按下列要求写出函数关系式: ①设(米),将表示成的函数关系式; A B ②设,将表示成的函数关系式. O (II)求梯形部件ABCD面积的最大值. 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为立方米,且.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为()千元.设该容器的建造费用为千元. (1)写出关于的函数表达式,并求该函数的定义域; (2)求该容器的建造费用最小时的. 如图,海岸线,现用长为的拦网围成一养殖场,其中. (1)若,求养殖场面积最大值; (2)若、为定点,,在折线内选点, 使,求四边形养殖场DBAC的最大面积. 由一个小区历年市场行情调查得知,某一种蔬菜在一年12个月内每月销售量(单位:吨)与上市时间(单位:月)的关系大致如图(1)所示的折线表示,销售价格(单位:元/千克)与上市时间(单位:月)的大致关系如图(2)所示的抛物线段表示(为顶点). (Ⅰ)请分别写出,关于的函数关系式,并求出在这一年内3到6月份的销售额最大的月份? (Ⅱ)图(1)中由四条线段所在直线围成的平面区域为,动点在内(包括边界),求的最大值; (Ⅲ) 由(Ⅱ),将动点所满足的条件及所求的最大值由加法运算类比到乘法运算(如类比为),试列出所满足的条件,并求出相应的最大值. (图1) (图2) 已知某种稀有矿石的价值(单位:元)与其重量(单位:克)的平方成正比,且克该种矿石的价值为元。 ⑴写出(单位:元)关于(单位:克)的函数关系式; ⑵若把一块该种矿石切割成重量比为的两块矿石,求价值损失的百分率; ⑶把一块该种矿石切割成两块矿石时,切割的重量比为多少时,价值损失的百分率最大。 (注:价值损失的百分率;在切割过程中的重量损耗忽略不计) 某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线的一部分,栏栅与矩形区域的边界交于点M、N,交曲线于点P,设 O (1)将(O为坐标原点)的面积表示成的函数; (2)若在处,取得最小值,求此时的值及的最小值. 某公司为了应对金融危机,决定适当进行裁员.已知这家公司现有职工2m人(60查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档