2011年四川省广安中考数学试题及答案

2011年四川省广安中考数学试题及答案

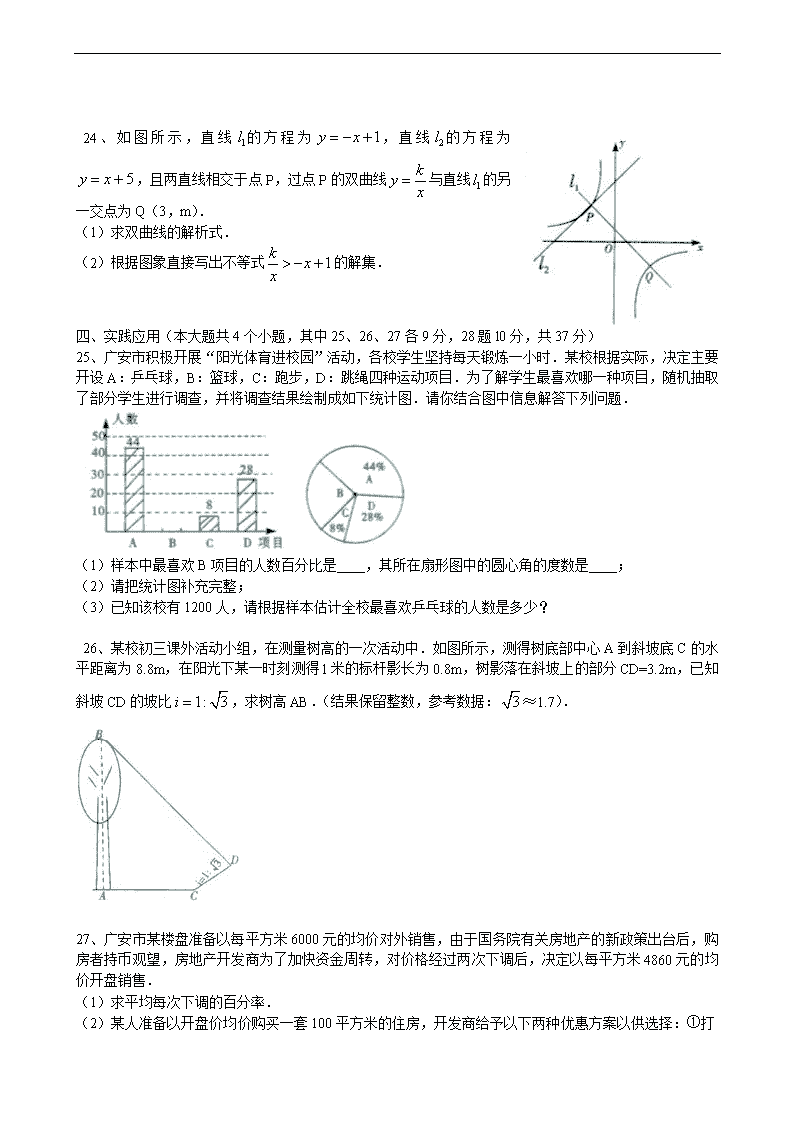
‎2011年四川省广安市中考数学试卷 一、选择题：每小题给出的四个选项中．只有一个选项符合题意要求．请将符合要求的选项的代号填涂在机读卡上（本大题共10个小题，每小题3分，共30分）‎ ‎1、的倒数是（　　）‎ ‎ A、 B、 C、± D、3 2、下列运算正确的是（　　）‎ ‎ A、 B、 C、 D、 3、已知样本数据l，0，6，l，2，下列说法不正确的是（　　）‎ ‎ A、中位数是6 B、平均数是2 C、众数是1 D、极差是6 4、从《中华人民共和国2010年国民经济和社会发展统计报告》中获悉，去年我国国内生产总值达397983亿元．请你以亿元为单位用科学记数法表示去年我国的国内生产总值为（结果保留两个有效数字）（　　）‎ ‎ A、 B、 C、 D、 5、下列几何图形：①角；②平行四边形；③扇形；④正方形，其中轴对称图形是（　　）‎ ‎ A、①②③ B、②③④ C、①③④ D、①②③④ 6、如图，圆柱的底面周长为6cm，AC是底面圆的直径，高BC=6cm，点P是母线BC上一点，且PC=BC．一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是（　　）‎ ‎ A、㎝ ‎ ‎ B、5cm ‎ C、㎝ ‎ D、7cm 7、下列命题中，正确的是（　　）‎ ‎ A、过一点作已知直线的平行线有一条且只有一条 B、对角线相等的四边形是矩形 C、两条边及一个角对应相等的两个三角形全等 D、位似图形一定是相似图形 8、在直角坐标平面内的机器人接受指令“[a，A]”（a≥0，0°＜A＜180°）后的行动结果为：在原地顺时针旋转A后，再向正前方沿直线行走口．若机器人的位置在原点，正前方为y轴的负半轴，则它完成一次指令[2，60°]后位置的坐标为（　　）‎ ‎ A、 B、 C、 D、 9、由n个相同的小正方体堆成的几何体，其视图如下所示，则n的最大值是（　　） ‎ ‎ A、18‎ ‎ B、19‎ ‎ C、20‎ ‎ D、21 ‎ ‎10、若二次函数，当时，y随x的增大而减小，则m的取值范围是（　　）‎ ‎ A、 B、 C、 D、 ‎ 二、填空题：请把最简答案直接填写在题后的横线上（本大题共10个小题，每小题3分，共30分）‎ ‎11、因式分解：=___________‎ ‎12、如图所示，直线a∥b，直线c与直线a，b分别相交于点A、点B，AM⊥b，垂足为点M，若∠l=58°，则∠2= ___________‎ ‎13、函数自变量x的取值范围是___________‎ ‎14、已知⊙与⊙的半径分别是方程的两实根，若⊙与⊙的圆心距d=5，则⊙与⊙的位置关系___________‎ ‎15、在一只不透明的口袋中放人只有颜色不同的白球6个，黑球4个，黄球n个，搅匀后随机从中摸取一个恰好是黄球的概率为，则放入的黄球总数n= ___________‎ ‎16、若凸n边形的内角和为1260°，则从一个顶点出发引的对角线条数是___________‎ ‎17、写出一个具体的y随x的增大而减小的一次函数解析式___________‎ ‎18、分式方程的解=___________‎ ‎19题图 ‎20题图 ‎12题图 ‎19、如图所示，若⊙O 的半径为13cm，点P是弦AB上一动点，且到圆心的最短距离为5cm，则弦AB的长为___________‎ ‎ 20、如图所示，直线OP经过点P（4，），过x轴上的点1、3、5、7、9、11…分别作x轴的垂线，与直线OP相交得到一组梯形，其阴影部分梯形的面积从左至右依次记为、…，则关于n的函数关系式是___________‎ 三、解答题（本大题共4个小题，第21小题7分，第22、23、24小题各8分．共31分）‎ ‎21、计算：‎ ‎22、先化简，然后从不等组的解集中，选取一个你认为符合题意的x的值代入求值．‎ ‎ 23、如图所示，在菱形ABCD中，∠ABC=60°，DE∥AC交BC的延长线于点E．‎ 求证：DE=BE．‎ ‎ ‎ ‎ 24、如图所示，直线的方程为，直线的方程为，且两直线相交于点P，过点P的双曲线与直线的另一交点为Q（3，m）．‎ ‎（1）求双曲线的解析式．‎ ‎（2）根据图象直接写出不等式的解集．‎ 四、实践应用（本大题共4个小题，其中25、26、27各9分，28题l0分，共37分）‎ ‎25、广安市积极开展“阳光体育进校园”活动，各校学生坚持每天锻炼一小时．某校根据实际，决定主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳四种运动项目．为了解学生最喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图．请你结合图中信息解答下列问题．‎ ‎ ‎ ‎（1）样本中最喜欢B项目的人数百分比是____，其所在扇形图中的圆心角的度数是____；‎ ‎（2）请把统计图补充完整；‎ ‎（3）已知该校有1200人，请根据样本估计全校最喜欢乒乓球的人数是多少？‎ ‎ ‎ ‎ 26、某校初三课外活动小组，在测量树高的一次活动中．如图所示，测得树底部中心A到斜坡底C的水平距离为8.8m，在阳光下某一时刻测得l米的标杆影长为0.8m，树影落在斜坡上的部分CD=3.2m，已知斜坡CD的坡比，求树高AB．（结果保留整数，参考数据：≈1.7）．‎ ‎ ‎ ‎27、广安市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售．‎ ‎（1）求平均每次下调的百分率．‎ ‎（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①‎ 打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？‎ ‎ ‎ ‎28、某园艺公司对一块直角三角形的花圃进行改造，测得两直角边长为6m、8m．现要将其扩建成等腰三角形，且扩充部分是以8m为直角边的直角三角形．求扩建后的等腰三角形花圃的周长．‎ ‎ ‎ 五、推理论证题（本题10分）‎ ‎ 29、如图所示，P是⊙O外一点，PA是⊙O的切线，A是切点，B是⊙O 上一点，且PA=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．‎ ‎（1）求证：PB是⊙O的切线；‎ ‎（2）求证：AQ•PQ=OQ•BQ；‎ ‎（3）设∠AOQ=α，若cosα= ，OQ=15，求AB的长．‎ 六、拓展探索题（本题12分）‎ ‎30、如图所示，在平面直角坐标系中，四边形ABCD是直角梯形，BC∥AD，∠BAD=90°，BC与y轴相交于点M，且M是BC的中点，A、B、D三点的坐标分别是A（），B（），D（3，0）．连接DM，并把线段DM沿DA方向平移到ON．若抛物线经过点D、M、N．‎ ‎（1）求抛物线的解析式．‎ ‎（2）抛物线上是否存在点P，使得PA=PC，若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎（3）设抛物线与x轴的另一个交点为E，点Q是抛物线的对称轴上的一个动点，当点Q在什么位置时有|QE-QC|最大？并求出最大值．‎ ‎ ‎ ‎2011年广安中考数学答案 一、 选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B C A D C B D C A C 二、 填空题 ‎11. 12. 32° 13. 14. 相交 15. 5 16. 6 17. 等（只要k<0即可） 18. 19. 24㎝ 20. ‎ 三、 解答题 ‎21. 解：原式=．‎ ‎22. 解：原式=，‎ 解不等式①，得，‎ 解不等式②，得，‎ ‎∴不等式组的解集为，‎ 取x=1时，原式=6．‎ 本题答案不唯一．‎ ‎23. 法一：证明：连接BD，‎ ‎∵四边形ABCD是菱形，∠ABC=60°，‎ ‎∴BD⊥AC，∠DBC=30°，‎ ‎∵DE∥AC，‎ ‎∴DE⊥BD，‎ 即∠BDE=90°，‎ ‎∴DE=BE．‎ 法二：∵四边形ABCD是菱形，∠ABC=60°，‎ ‎∴AD∥BC，AC=AD，‎ ‎∵AC∥DE，‎ ‎∴四边形ACED是菱形，‎ ‎∴DE=CE=AC=BC，‎ ‎∴DE=BE．‎ ‎24. 解：（1）联立列方程组得，‎ 解得，‎ 即P ‎∴，‎ ‎∴双曲线的解析式；‎ ‎（2）或．‎ ‎25. 解：（1）样本中最喜欢B项目的人数百分比是1-44%-8%-28%=20%，其所在扇形图中的圆心角的度数是360°×20%=72°．‎ ‎（2）B组人数44÷44%×20=20人，画图如下：‎ ‎（3）1200×44%=528人，全校最喜欢乒乓球的人数大约是528人．‎ 故答案为20%，72°．‎ ‎26. 解：过点作DE⊥AB，DF⊥AC，垂足分别为E，F，如图，‎ ‎∵斜坡CD的坡比，即tan∠DCF=，‎ ‎∴∠DCF=30°，‎ 而CD=3.2m，‎ ‎∴DF=CD=1.6m，CF=DF=m，‎ ‎∵AC=8.8m，‎ ‎∴DE=AC+CF=8.8+，‎ ‎∴，‎ ‎∴BE=，‎ ‎∴AB=BE+AE=1≈16m．‎ 答：树高AB为16m．‎ ‎27. 解：（1）设平均每次下调的百分率为x，‎ 则，‎ 解得或（舍去），‎ 故平均每次下调的百分率为10%；‎ ‎（2）方案①购房优惠：4860×100×0.02=9720（元）‎ 方案②购房优惠：80×100=8000（元），‎ 故选择方案①更优惠．‎ ‎28. 解：在Rt△ABC中，∵AC=8m，BC=6m，‎ ‎∴AB=10m，‎ ‎（1）当AB=AD时，CD=6m，‎ ‎△ABD的周长为32m；‎ ‎（2）当AB=BD时，CD=4m，AD=m，‎ ‎△ABD的周长是（20+）m；‎ ‎（3）当DA=DB时，设AD=x，则CD=x-6，‎ 则，‎ ‎∴，‎ ‎∴△ABD的周长是m，‎ 答：扩建后的等腰三角形花圃的周长是32m或 20+ m或 m．‎ ‎29. 解：（1）证明：连接OP，与AB交与点C．‎ ‎∵PA=PB，OA=OB，OP=OP，‎ ‎∴△OAP≌△OBP（SSS），‎ ‎∴∠OBP=∠OAP，‎ ‎∵PA是⊙O的切线，A是切点，‎ ‎∴∠OAP=90°，‎ ‎∴∠OBP=90°，即PB是⊙O的切线；‎ ‎（2）∵∠Q=∠Q，∠OAQ=∠QBP=90°，‎ ‎∴△QAO∽△QBP，‎ ‎∴ ，即AQ•PQ=OQ•BQ；‎ ‎（3）在Rt△OAQ中，∵OQ=15，cosα=，‎ ‎∴OA=12，AQ=9，‎ ‎∴QB=27；‎ ‎∵ = ，‎ ‎∴PQ=45，即PA=36，‎ ‎∴OP=；‎ ‎∵PA、PB是⊙O的切线，‎ ‎∴OP⊥AB，AC=BC，‎ ‎∴PA•OA=OP•AC，即36×12=•AC，‎ ‎∴AC=，故AB=．‎ ‎30. 解：（1）∵BC∥AD，B（-1，2），M是BC与x轴的交点，∴M（0，2），‎ ‎∵DM∥ON，D（3，0），∴N（-3，2），则，解得，∴；‎ ‎（2）连接AC交y轴与G，∵M是BC的中点，∴AO=BM=MC，AB=BC=2，∴AG=GC，即G（0，1），‎ ‎∵∠ABC=90°，∴BG⊥AC，即BG是AC的垂直平分线，要使PA=PC，即点P在AC的垂直平分线上，故P在直线BG上，‎ ‎∴点P为直线BG与抛物线的交点，‎ 设直线BG的解析式为，则，解得，∴，‎ ‎∴，解得，，‎ ‎∴点P（）或P（），‎ ‎（3）∵，∴对称轴，‎ 令，解得，，∴E（，0），‎ 故E、D关于直线对称，∴QE=QD，∴|QE-QC|=|QD-QC|，‎ 要使|QE-QC|最大，则延长DC与相交于点Q，即点Q为直线DC与直线的交点，‎ 由于M为BC的中点，∴C（1，2），设直线CD的解析式为y=kx+b，‎ 则，解得，∴，‎ 当时，，‎ 故当Q在（）的位置时，|QE-QC|最大，‎ 过点C作CF⊥x轴，垂足为F，则CD=．‎