中考数学模拟试卷

中考数学模拟试卷

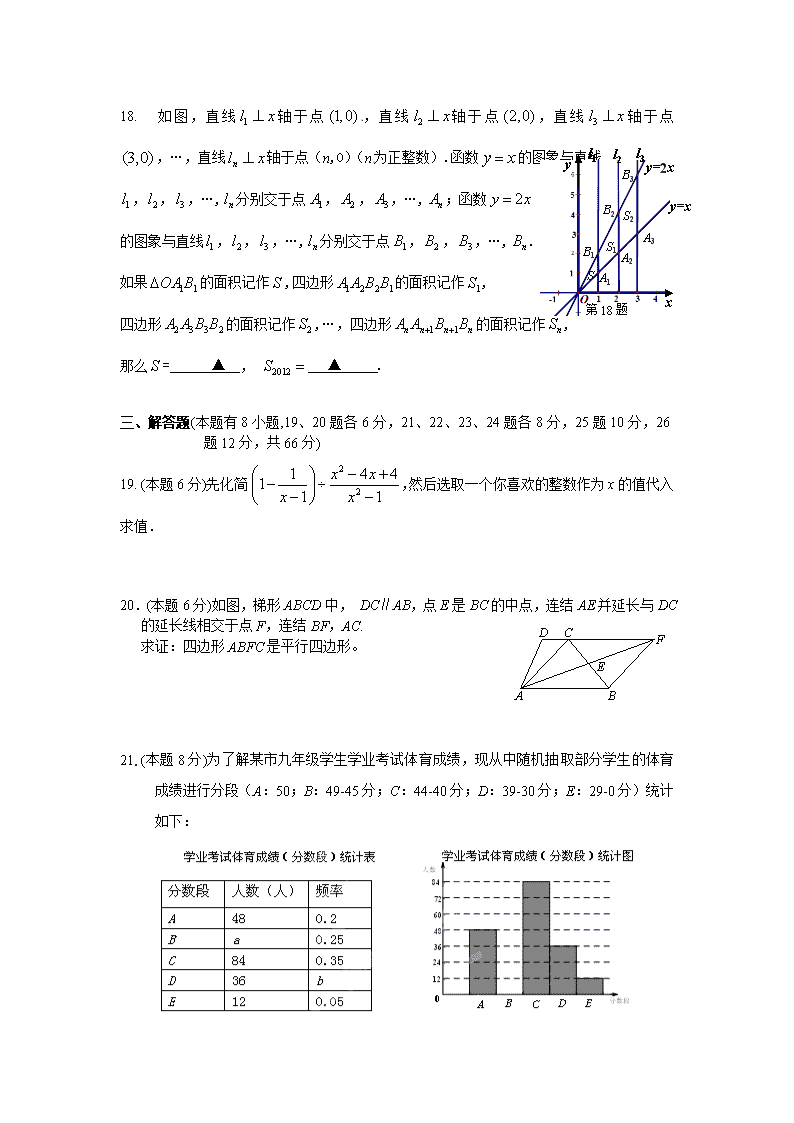
宁波市2012年中考数学模拟试卷 一、选择题(本题有12小题，每小题3分,共36分,在每小题给出的四个中只有一个符合题目要求)‎ ‎1．有理数的倒数是………（ ）‎ A． B． C． D．‎ ‎2. 函数中，自变量的取值范围是（ ）‎ ‎ A. B. C. D. ‎ ‎3. 下列运算中，结果正确的是（ ） ‎ ‎ A. B. C. D. ‎ ‎4. 第六次全国人口普查数据显示，全国总人口初步统计为134100万人，134100万人保留三个有效数字可表示为（ ）‎ A.1.34‎‎×105人 B. 1.34×109人 C. 1.35×105人 D. 1.35×109人 ‎5. 如图，下列水平放置的几何体中，左视图不是矩形的是（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎6. 一枚质地均匀的正方体骰子，其六个面上分别刻有1、2、3、4、5、6六个数字，投掷这个骰子一次，则向上一面的数字不小于3的概率是( )‎ A. B. C. D. ‎ ‎7. 在一次学校运动会上，参加男子跳高的15名运动员的成绩如下表：‎ 跳高成绩(m)‎ ‎1.20‎ ‎1.25‎ ‎1.30‎ ‎1.35‎ ‎1.40‎ ‎1.45‎ 跳高人数 ‎1‎ ‎3‎ ‎2‎ ‎3‎ ‎5‎ ‎1‎ 这些运动员跳高成绩的中位数和众数分别是（ ）‎ A C B D O 第8题图 ‎ A．1.35，1.40 B．1.40，‎1.35 C．1.40，1.40 D．3，5‎ ‎8．如图，是的外接圆，是的直径，若的半径为， ，则的值是（ ）‎ ‎（第9题）‎ A B C A． B． C． D．‎ ‎9. 在Rt△ABC中，∠C=90°，AC=8，BC=6，两等圆⊙A，⊙B 外切，那么图中两个扇形（即阴影部分）的面积之和为（ ）‎ A． B． C． D．‎ ‎10．如果一个三角形能够分成两个与原三角形都相似的三角形，我们把这样的三角形称为孪生三角形，那么孪生三角形是（ ）‎ A．不存在 B．等腰三角形 ‎ C．直角三角形 D．等腰三角形或直角三角形 ‎11．如图所示，P是菱形ABCD的对角线AC上一动点，过P垂直于AC的直线交菱形ABCD的边于M、N两点，设AC=2，BD=1，AP=x，则△AMN的面积为y，则y关于x的函数图象的大致形状是（　　）‎ A、 B、 ‎ ‎ C、 D、 ‎ ‎12. 如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．‎ 下列结论：①tan∠ADB=2；②图中有4对全等三角形；‎ ‎③若将△DEF沿EF折叠，则点D不一定落在AC上；‎ ‎④BD=BF；⑤，上述结论中正确的个数是（　　）‎ ‎ A. 4个 B. 3个 C. 2个 D. 1个 二、填空题（本题有6小题，每题3分，共18分）‎ ‎13. 因式分解： b2–9 = ▲ ‎ ‎14. 如果点P（）关于原点的对称点为（–2，4），则x+y= ▲ .‎ 第16题 ‎15. 如图所示：用一个半径为60cm，圆心角为150°的扇形围成一个圆锥，则这个圆锥的底面半径为　 ▲ 　cm．‎ ‎（第15题图）‎ ‎16. 某中学在校内安放了几个圆柱形饮水桶的木制支架（如图①），若不计木条的厚度，其俯视图如图②所示，已知AD垂直平分BC，AD=BC=40cm，则圆柱形饮水桶的底面半径的最大值是 ▲ cm. ‎ ‎17．如图，直线与双曲线（）交于点．将直线向下平移6个O x y A B C 单位后，与双曲线（）交于点，与轴交于点C，则C点的坐标为_▲__________；若，则 ▲ ．‎ ‎18.如图，直线轴于点，直线轴于点，直线轴于点，…，直线轴于点（n,0）（n为正整数）.函数的图象与直线 l1‎ l2‎ l3‎ y=x y=2x S S1‎ S2‎ A1‎ B1‎ A2‎ B2‎ A3‎ B3‎ 第18题 x y ‎，，，…,分别交于点，，，…,；函数 的图象与直线，，，…,分别交于点，，，…,.‎ 如果的面积记作,四边形的面积记作,‎ 四边形的面积记作,…，四边形的面积记作,‎ 那么= ▲ ， ▲ .‎ 三、解答题(本题有8小题,19、20题各6分，21、22、23、24题各8分，25题10分，26题12分，共66分)‎ ‎19. (本题6分)先化简，然后选取一个你喜欢的整数作为x的值代入求值．‎ ‎20．(本题6分)D C F E A B 如图，梯形ABCD中， DC∥AB，点E是BC的中点，连结AE并延长与DC的延长线相交于点F，连结BF，AC.‎ 求证：四边形ABFC是平行四边形。 ‎ ‎21. (本题8分)为了解某市九年级学生学业考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段（A：50；B：49-45分；C：44-40分；D：39-30分；E：29-0分）统计如下：‎ ‎ ‎ 根据上面提供的信息，回答下列问题：‎ ‎（1）在统计表中，a的值为 ，b的值为 ，并将统计图补充完整（温馨提示：作图时别忘了用‎0.5毫米及以上的黑色签字笔涂黑）；‎ ‎（2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数. ”请问：甲同学的体育成绩应在什么分数段内？ （填相应分数段的字母）‎ ‎（3）如果把成绩在40分以上（含40分）定为优秀，那么该市今年8875 名九年级学生中体育成绩为优秀的学生人数约有多少名？‎ ‎22.(本题8分)如图，已知AB是⊙O的直径，锐角∠DAB的平分线AC交⊙O 于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．‎ ‎（1）求证：直线CD为⊙O的切线；‎ ‎（2）当AB=2BE，且CE=时，求AD的长．‎ ‎23.(本题8分) 如图，小明在楼上点A处观察旗杆BC，测得旗杆顶部B的仰角为30°，测得旗杆底部C的俯角为60°，已知点A距地面的高AD为‎12m．求旗杆的高度．‎ ‎24.（本题8分）如图①，将一张直角三角形纸片折叠，使点与点重合，这时为折痕，为等腰三角形；再继续将纸片沿的对称轴折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”.‎ 图① 图② 图③‎ ‎ ‎ ‎（1）如图②，正方形网格中的能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；‎ ‎（2）如图③，在正方形网格中，以给定的为一边，画出一个斜三角形，使其顶点在格点上，且折成的“叠加矩形”为正方形；‎ ‎（3）若一个三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是什么？‎ ‎25.(本题10分) 为发展“低碳经济”，某单位进行技术革新, 让可再生资源重新利用. 从今年1月1日开始,该单位每月再生资源处理量y（吨）与月份x之间成如下一次函数关系：‎ 月份x ‎1‎ ‎2‎ 再生资源处理量y（吨）‎ ‎40‎ ‎50‎ 月处理成本z（元）与每月再生资源处理量y（吨）之间的函数关系可近似地表示为：‎ ‎ z =,每处理一吨再生资源得到的新产品的售价定为100元.‎ ‎（1）求出该单位每月再生资源处理量y（吨）与月份x之间的函数关系式；求出月处理成本z（元）与月份x之间的函数关系式。‎ ‎（2）该单位哪个月获得利润最大？最大是多少？‎ ‎（3）随着人们环保意识的增加，该单位需求的可再生资源数量受限。今年三月份的再生资源处理量比二月份减少了m % ,该新产品的产量也随之减少，其售价比二月份的售价增加了‎0.6m %.五月份，该单位得到国家科委的技术支持，使月处理成本比二月份的降低了20% ，如果该单位在保持三月份的再生资源处理量和新产品售价的基础上，而其利润与二月份的利润一样,求m ．( m保留整数) （）‎ ‎26. 在平面直角坐标系xOy中，已知二次函数y1=ax2+3x+c的图像经过原点及点A（1,2）， ‎ ‎ 与x轴相交于另一点B。‎ ‎（1）求：二次函数y1的解析式及B点坐标；‎ ‎（2）若将抛物线y1以x=3为对称轴向右翻折后，得到一个新的二次函数y2,已知二次函数y2‎ 与x轴交于两点，其中右边的交点为C点. 点P在线段OC上，从O点出发向C点运动，过P点作x轴的垂线，交直线AO于D点，以PD为边在PD的右侧作正方形PDEF（当P点运动时，点D、点E、点F也随之运动）；‎ ‎①当点E在二次函数y1的图像上时，求OP的长。‎ ‎②若点P从O点出发向C点做匀速运动，速度为每秒1个单位长度，同时线段OC上另一个点Q从C点出发向O点做匀速运动，速度为每秒2个单位长度（当Q点到达O点时停止运动，P点也同时停止运动）。过Q点作x轴的垂线，与直线AC交于G点，以QG为边在QG的左侧作正方形QGMN（当Q点运动时，点G、点M、点N也随之运动），若P点运动t秒时，两个正方形分别有一条边恰好落在同一条直线上（正方形在x轴上的边除外），求此刻t的值。‎