- 2021-04-27 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019九年级数学上册 第23章 图形的相似 23平行线分线段成比例
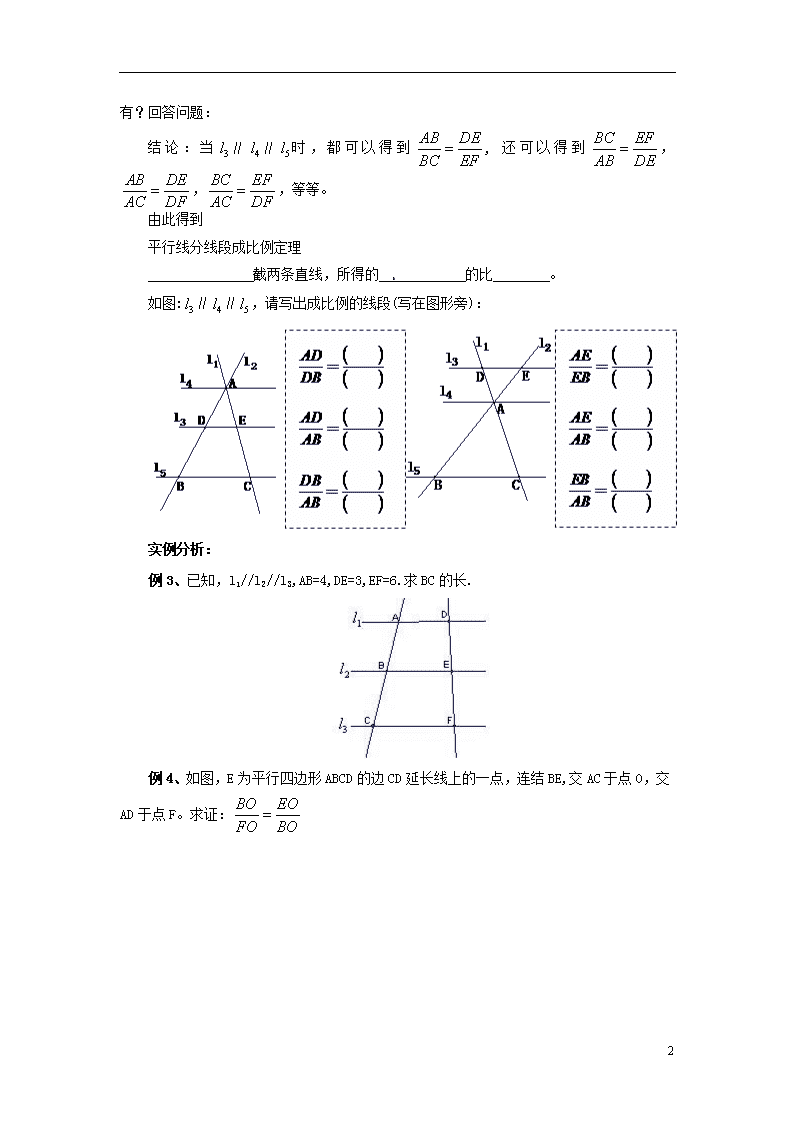
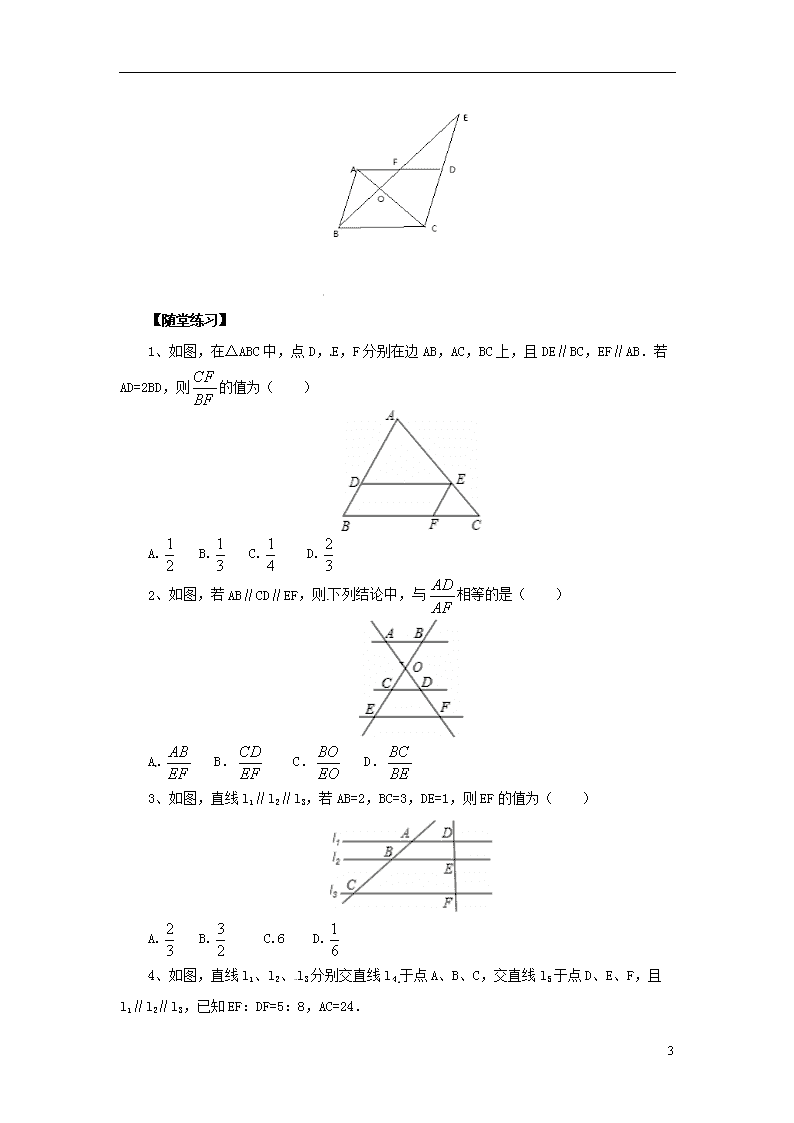
23.1.2 平行线分线段成比例 【学习目标】 1. 平行线分线段成比例定理及其推论。 2. 会应用平行线分线段成比例定理写比例式、计算。 3.经历探究平行线分线段成比例定理的过程,培养分析归纳能力。 【学习重难点】 平行线分线段成比例定理及其推论。 【学习过程】 一、课前准备 1、什么叫比例线段?比例有哪些性质? 二、学习新知 自主学习: 1、做一做:右图是单行本的 一部分,“8 mm×21 lines”是什么含义?再在其上画一条直线,量一量夹在相邻 两条平行线间的线段大小有什么关系?“8 mm”表示:___________________。 结论:如果一组平行线在一条直线上截得的线段相等,那么在另一条直线上截得的线段____________。 2、如果一组平行线间的距离不相等,如图∥∥,它们在直线上截得线段AB、BC,在直线上截得线段DE、EF。 量一量,算一算: (度量精确到0.1mm,计算保留一位小数) ①、,,; ,,; ②、,; ③、,; 根据①、②、③的计算结果,你得到的结论: 4 3、仔细观察几何画板的演示,留心数据的变化情况,在演示过程中你发现什么规律没有?回答问题: 结论:当∥∥时,都可以得到, 还可以得到,,,等等。 由此得到 平行线分线段成比例定理 截两条直线,所得的 的比 。 如图:∥∥,请写出成比例的线段(写在图形旁): 实例分析: 例3、已知,l1//l2//l3,AB=4,DE=3,EF=6.求BC的长. 例4、如图,E为平行四边形ABCD的边CD延长线上的一点,连结BE,交AC于点O,交AD于点F。求证: 4 【随堂练习】 1、如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为( ) A. B. C. D. 2、如图,若AB∥CD∥EF,则下列结论中,与相等的是( ) A. B. C. D. 3、如图,直线l1∥l2∥l3,若AB=2,BC=3,DE=1,则EF的值为( ) A. B. C.6 D. 4、 如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,已知EF:DF=5:8,AC=24. 4 (1)求AB的长; (2)当AD=4,BE=1时,求CF的长. 【中考连线】 如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,如果DE:EF=3:5,AC=24,则BC= . 【参考答案】 随堂练习 1、A 2、D 3、B 4、AB=9,CF=4 中考连线 BC=15. 4查看更多