- 2021-04-27 发布 |
- 37.5 KB |
- 3页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
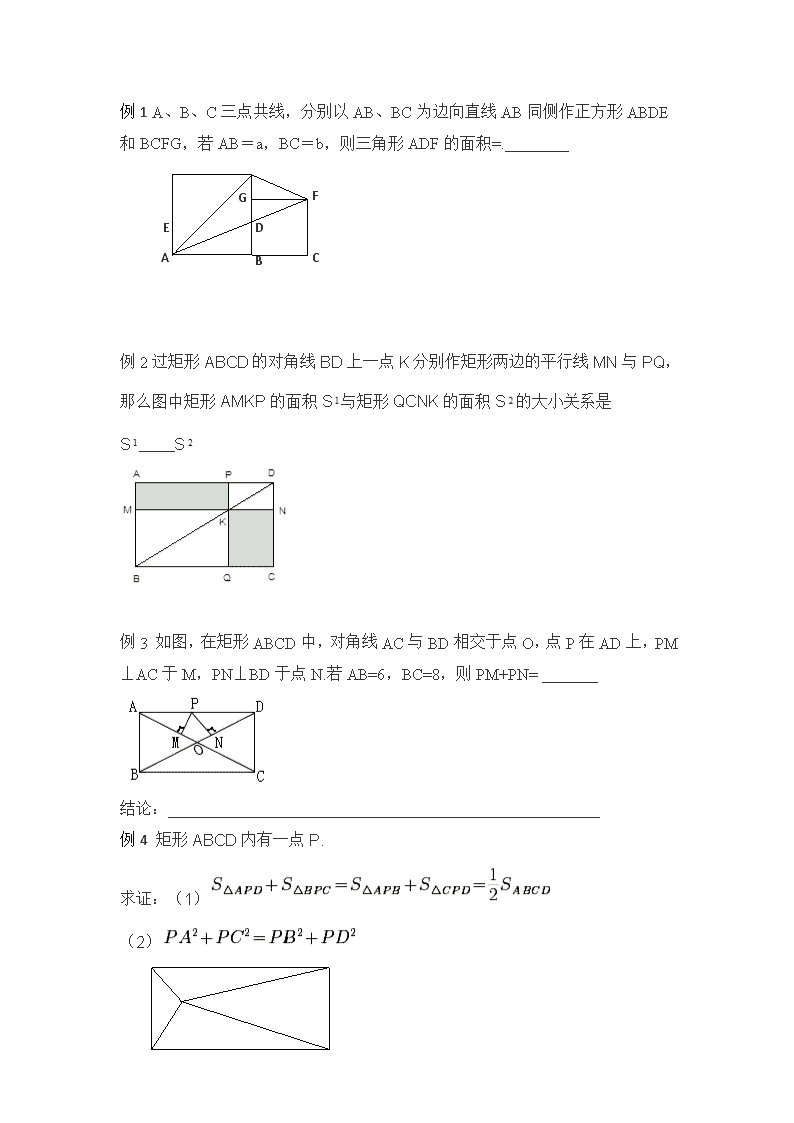
中考复习几何综合之面积问题
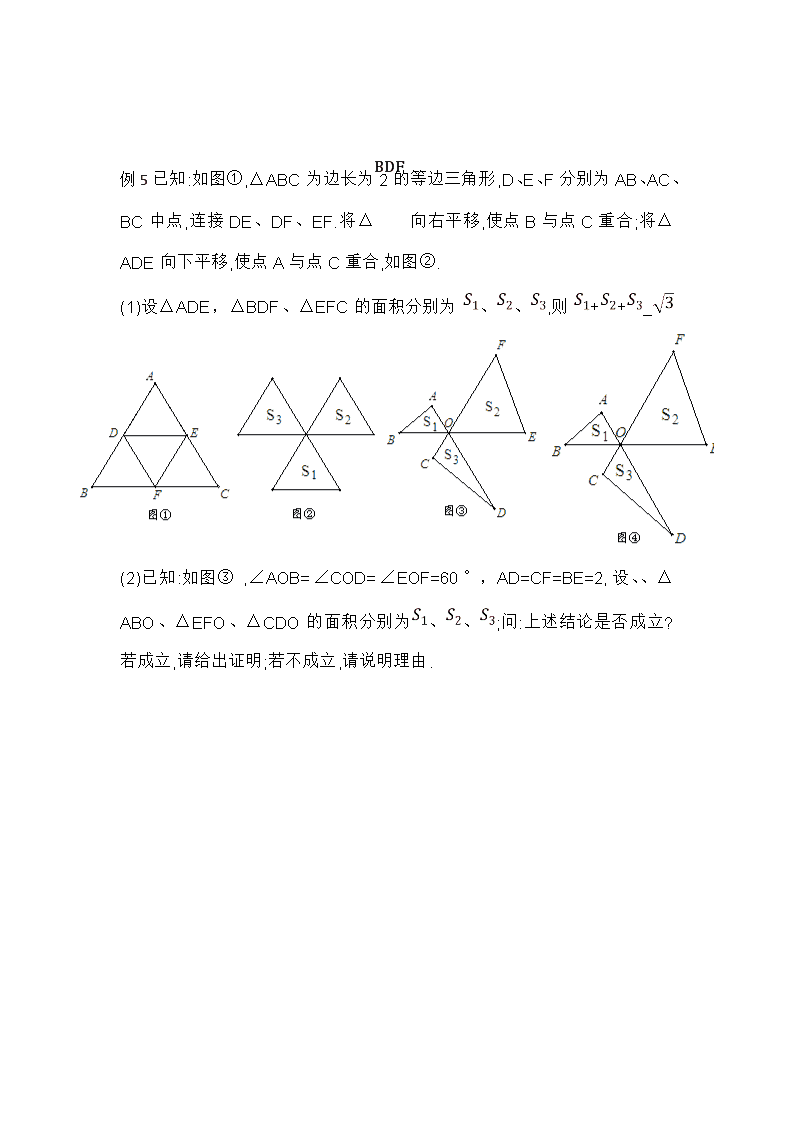
几何综合之面积问题—涉及面积问题的基本模型(6个) (1)燕尾模型 (2)共边定理 (3)平行四边形 (4)四个平行四边形 (5)任意点 (6)蝴蝶翅膀 总结:像燕尾与蝴蝶翅膀属于重点,常考内容 常用方法:直接求、总减去空、割补法 E D 例1 A、B、C三点共线,分别以AB、BC为边向直线AB同侧作正方形ABDE和BCFG,若AB=a,BC=b,则三角形ADF的面积=.________ G C F B A 例2过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形 AMKP的面积S与矩形QCNK的面积S的大小关系是S S 例3 如图,在矩形ABCD中,对角线AC与BD相交于点O,点P在AD上,PM⊥AC于M,PN⊥BD于点N.若AB=6,BC=8,则PM+PN= _______ 结论:______________________________________________________ 例4 矩形ABCD内有一点P. 求证:(1) (2) 例5已知:如图①,△ABC为边长为2的等边三角形,D、E、F分别为AB、AC、BC中点,连接DE、DF、EF.将△BDF向右平移,使点B与点C重合;将△ADE向下平移,使点A与点C重合,如图②. (1)设△ADE,△BDF、△EFC的面积分别为 、、,则 ++_ (2)已知:如图③ ,∠AOB=∠COD=∠EOF=60°,AD=CF=BE=2,设、、△ABO、△EFO、△CDO的面积分别为、、;问:上述结论是否成立?若成立,请给出证明;若不成立,请说明理由.查看更多