高考指数对数及例题

高考指数对数及例题

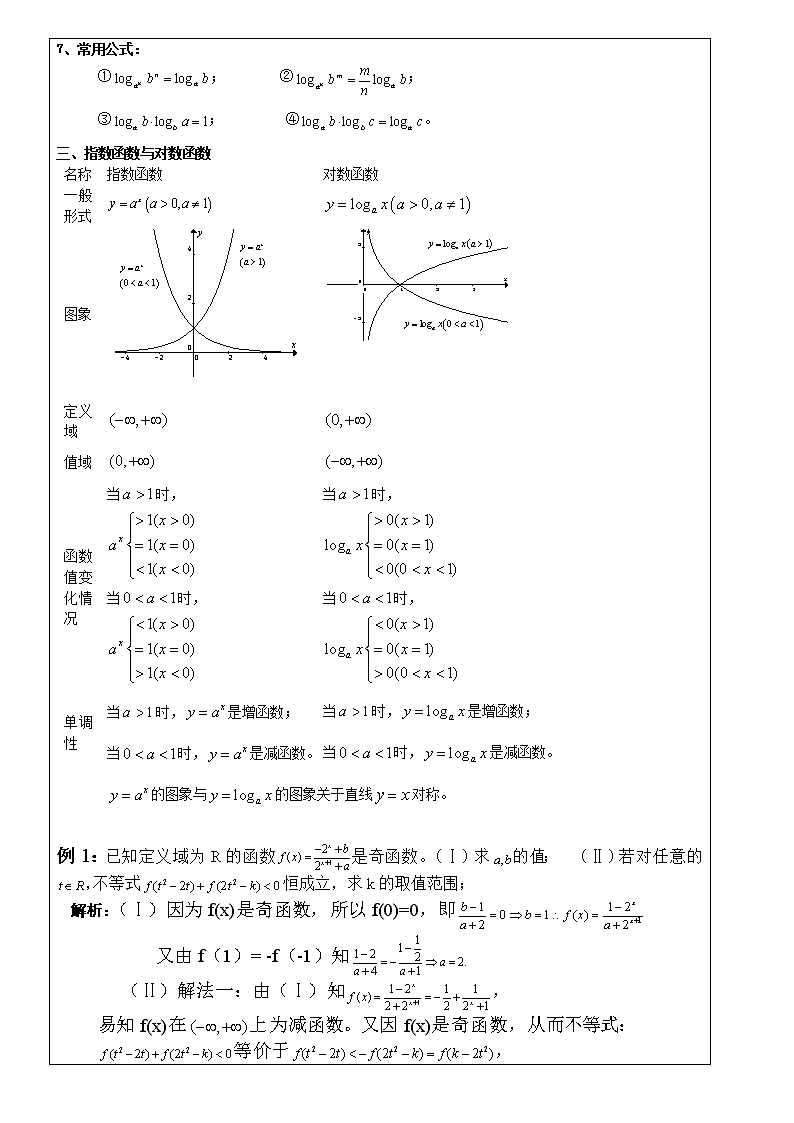
‎ 龙文学校个性化辅导教案提纲 教师： 学生： 时间： 年_ 月 日 段 授课目的与考点分析： ‎ 指数函数、对数函数是高考考查的重点内容之一，本节主要帮助考生掌握两种函数的概念、图象和性质并会用它们去解决某些简单的实际问题.‎ 一、分数指数与根式 ‎1、两组常用等式：‎ 当（）为奇数时，=；‎ ‎ 当（）为正偶数时，=‎ ‎2、正数的分数指数幂的意义：‎ ‎ 当，、，且时，；，。‎ ‎3、幂的运算法则：‎ ‎ 若、，，，则 ‎ ；；；。‎ 二、对数：‎ ‎1、定义：如果（且），那么就叫做以为底N的对数，记作（且）‎ ‎2、对数恒等式：‎ ‎ （且，）； （且）。‎ ‎3、对数性质：‎ ‎ 负数和零没有对数；1的对数是零，底的对数是1；即，。‎ ‎4、对数运算法则：‎ ‎ 若且，，则 ‎； ；‎ ‎ ； 。‎ ‎5、换底公式：（且，且，）‎ ‎6、特殊对数：‎ ‎ 以为底的对数，叫做自然对数，记作。‎ ‎ 以10为底的对数，叫做常用对数，记作。‎ ‎7、常用公式：‎ ‎ ①； ②；‎ ‎ ③； ④。‎ 三、指数函数与对数函数 名称 指数函数 对数函数 一般形式 图象 定义域 值域 函数值变化情况 当时，‎ 当时，‎ 当时，‎ 当时，‎ 单调性 当时，是增函数；‎ 当时，是减函数。‎ 当时，是增函数；‎ 当时，是减函数。‎ 的图象与的图象关于直线对称。‎ 例1：已知定义域为R的函数是奇函数。（Ⅰ）求的值； （Ⅱ）若对任意的，不等式恒成立，求k的取值范围；‎ 解析：（Ⅰ）因为f(x)是奇函数，所以f(0)=0，即 ‎ 又由f（1）= -f（-1）知 ‎ （Ⅱ）解法一：由（Ⅰ）知，‎ 易知f(x)在上为减函数。又因f(x)是奇函数，从而不等式： ‎ 等价于，‎ 因为减函数，由上式推得：．即对一切有：，‎ 从而判别式 解法二：由（Ⅰ）知．又由题设条件得:　，‎ ‎　　 即　：，‎ 整理得　上式对一切均成立，‎ 从而判别式 例2：定义在R上的单调函数f(x)满足f(3)=log3且对任意x，y∈R都有f(x+y)=f(x)+f(y)．‎ ‎(1)求证f(x)为奇函数；‎ ‎(2)若f(k·3)+f(3-9-2)＜0对任意x∈R恒成立，求实数k的取值范围．‎ 解: (1)证明：f(x+y)=f(x)+f(y)(x，y∈R)，　　　　　　 ①‎ 令x=y=0，代入①式，得f(0+0)=f(0)+f(0)，即 f(0)=0．‎ 令y=-x，代入①式，得 f(x-x)=f(x)+f(-x)，又f(0)=0，‎ 则有0=f(x)+f(-x)．即f(-x)=-f(x)对任意x∈R成立，‎ 所以f(x)是奇函数．‎ ‎(2)解：f(3)=log3＞0，即f(3)＞f(0)，又f(x)在R上是单调函数，所以f(x)在R上是增函数，‎ 又由(1)f(x)是奇函数．f(k·3)＜-f(3-9-2)=f(-3+9+2)， ‎ ‎∴ k·3＜-3+9+2，3-(1+k)·3+2＞0对任意x∈R成立．‎ 令t=3＞0，问题等价于t-(1+k)t+2＞0‎ 对任意t＞0恒成立．‎ R恒成立．‎ 四、本次课后作业：‎ 五、学生对于本次课的评价：‎ ‎○特别满意 ○满意 ○一般 ○差 六、教师评定 ‎1.学生上次作业评价： ○好 ○较好 ○一般 ○差 2.学生本次上课情况评价： ○好 ○较好 ○一般 ○差 学生签字： 龙文学校教务处签字：‎