- 2021-04-27 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级上册数学课件-5 扇形 ︳人教新课标 (共21张PPT)
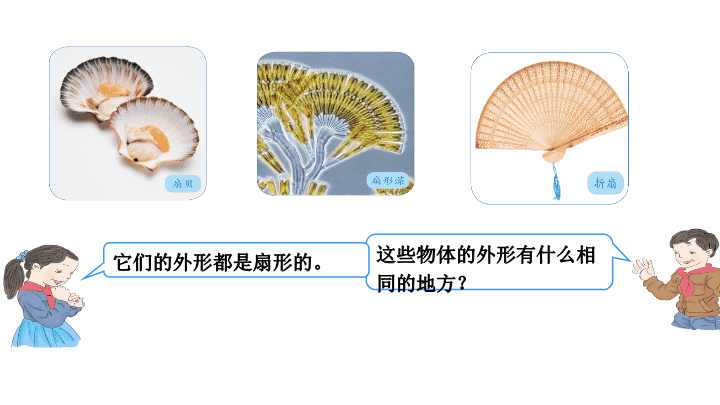
圆 扇形 云南省昌宁思源实验学校 教师:李绍丽 这些物体的外形有什么相 同的地方? 它们的外形都是扇形的。 扇 形 学习目标 1、结合生活中的物品,认识扇形,识记扇形的各部 分名称。 2、知道圆心角和半径的变化会带来扇形大小的变化 3、组1至组3层同学:推导出扇形面积计算方法。 组4至6层的同学模仿,运用。 尝试学习 1、分组自学,完成以下练习: (1)圆上A、B两点之间的部分叫做( ),读作“( )。” (2)一条( )和经过这条弧两端的两条( )所围成的 图形叫做( ) (3)像∠AOB这样,顶点在圆心的角叫做( ) (4)看图可以发现,在同一圆中,扇形的大小与这个扇形 的( )的大小有。 以下(组1、组2、组3必做,其他组选做) (5)扇形面积计算公式(S扇= )。 1、分组自学,完成以下练习: (1)圆上A、B两点之间的部分叫做( 弧 ),读作“( 弧AB )。” (2)一条(弧)和经过这条弧两端的两条(半径)所围 成的图形叫做( 扇形)。 (3)像∠AOB这样,顶点在圆心的角叫做(圆心角) (4)看图可以发现,在同一圆中,扇形的大小与这个扇 形的(圆心角)的大小有关。 以下(组1、组2、组3必做,其他组选做) (5)扇形面积计算公式(S扇= ∏r 2 )。360 n A B O 圆心角 半 径 半 径 弧 图上A、B两点之间的部分 叫做弧,读作“弧AB”。 一条弧和经过这条弧两端 的两条半径所围成的图形叫做 扇形。 顶点在圆心的角叫做圆心角。 A B C D O O O O 下面各图中,哪些是扇形? 在同一个圆中,扇形的大小与 什么有关系呢? 我发现在同一个圆中,扇形 的大小与这个扇形的圆心角 的大小有关。 180° 90° 以半圆为弧的扇形的圆心角是多少度? 以 圆为弧的扇形呢?4 1 以半圆为弧的扇形的 圆心角是180°。 360× =90(度)4 1 思考: 如果要知道圆心角分别为90 º、180º的扇形 面积是多少?先要知道什么? 下面圆中的扇形面积各是圆面积的几分之几? 并说明理由。 180º 90º 思考3: 圆心角是nº的扇形面积是圆面积的几分之几? 圆心角为nº的扇形面积是圆面积的 360 n 360 n r² 如果用字母表示:S表示扇形的面积,n表示圆 心角的度数,r表示圆半径 S = 那么扇形面积公式 r=10cm 圆心角是180度 r=3cm 圆心角是90度 计算扇形的面积 归纳 总结 1、一条弧和经过这条弧两端的两条半径 所围成的图形叫做扇形。 2、顶点在圆心的角叫做圆心角。在同一 个圆中,扇形的大小与这个扇形的圆 心角的大小有关。 3、如果用S表示扇形的面积,n表示圆 心角的度数,r表示圆的半径,则扇形 的面积S= πr 2360 n 当堂检测 ㈠基础题(20分)1、将下图中是扇形的序号写在考括号里( )。 A B C D 2、计算扇形面积(10分) r=3cm 圆心角是60度 ㈡组1、2、3必做,其他选做。计算阴影部分的面积。 (10分) 当堂检测 ㈠基础题(20分) 1、将下图中是扇形的序号写在考括号里( C D ) 。 A B C D 2、计算扇形面积(10分) r=3cm 圆心角是60度 ×32 × 3.14 = × 9 × 3.14 =1.5 × 3.14 =4.71(cm2) 360 60 6 1 • ㈡组1、2、3必做,其他选做。计 算阴影部分的面积。 (10分) 3.14×42÷2-3.14×(4-1)2÷2 =25.12-14.13 =10.99(dm2) • 通过课前预习和今天的学习你还知道扇形的那些 知识,我们一起分享。查看更多