高中数学人教a版必修五第三章不等式学业分层测评16word版含答案
学业分层测评(十六)
(建议用时:45 分钟)
[学业达标]
一、选择题
1.设 M=x2,N=-x-1,则 M 与 N 的大小关系是( )
A.M>N B.M=N
C.M
0.
∴M>N.
【答案】 A
2.某校对高一美术生划定录取分数线,专业成绩 x 不低于 95 分,文化课总
分 y 高于 380 分,体育成绩 z 超过 45 分,用不等式(组)表示就是( )
A.
x≥95,
y≥380,
z>45
B.
x≥95,
y>380,
z≥45
C.
x>95,
y>380,
z>45
D.
x≥95,
y>380,
z>45
【解析】 由题中 x 不低于 95,即 x≥95,
y 高于 380,即 y>380,
z 超过 45,即 z>45.
【答案】 D
3.设 a>1>b>-1,则下列不等式中恒成立的是( )
A.1
a<1
b B.1
a>1
b
C.a2>2b D.a>b2
【解析】 A 错,例如 a=2,b=-1
2
时,1
a
=1
2
,1
b
=-2,此时,1
a>1
b
;
B 错,例如 a=2,b=1
2
时,1
a
=1
2
,1
b
=2,此时,1
a<1
b
;
C 错,例如 a=5
4
,b=15
16
时,a2=25
16
,2b=30
16
,此时 a2<2b;
由 a>1,b2<1 得 a>b2,D 正确.
【答案】 D
4.(2016·安徽六校联考)若1
a<1
b<0,则下列不等式:①a+b|b|;③a0,所以 a+b|1
b|,两边同乘|ab|,得|b|>|a|,故②错误;由①②知|b|>|a|,
a<0,b<0,那么 a>b,即③错误,故选 B.
【答案】 B
5.设α∈ 0,π
2 ,β∈ 0,π
2 ,则 2α-β
3
的范围是( )
A. 0,5
6π B.
-π
6
,5
6π
C.(0,π) D.
-π
6
,π
【解析】 0<2α<π,0≤β
3
≤π
6
,
∴-π
6
≤-β
3
≤0,由同向不等式相加得到-π
6<2α-β
3<π.
【答案】 D
二、填空题
6.已知 x<1,则 x2+2 与 3x 的大小关系为________.
【解析】 (x2+2)-3x=(x-1)(x-2),
因为 x<1,
所以 x-1<0,x-2<0,
所以(x-1)(x-2)>0,所以 x2+2>3x.
【答案】 x2+2>3x
7.给出的四个条件:①b>0>a;②0>a>b;③a>0>b;④a>b>0,能得出1
a<1
b
成
立的是________.
【解析】 由1
a<1
b
,可得1
a
-1
b<0,即b-a
ab <0,
故①②④可推出1
a<1
b.
【答案】 ①②④
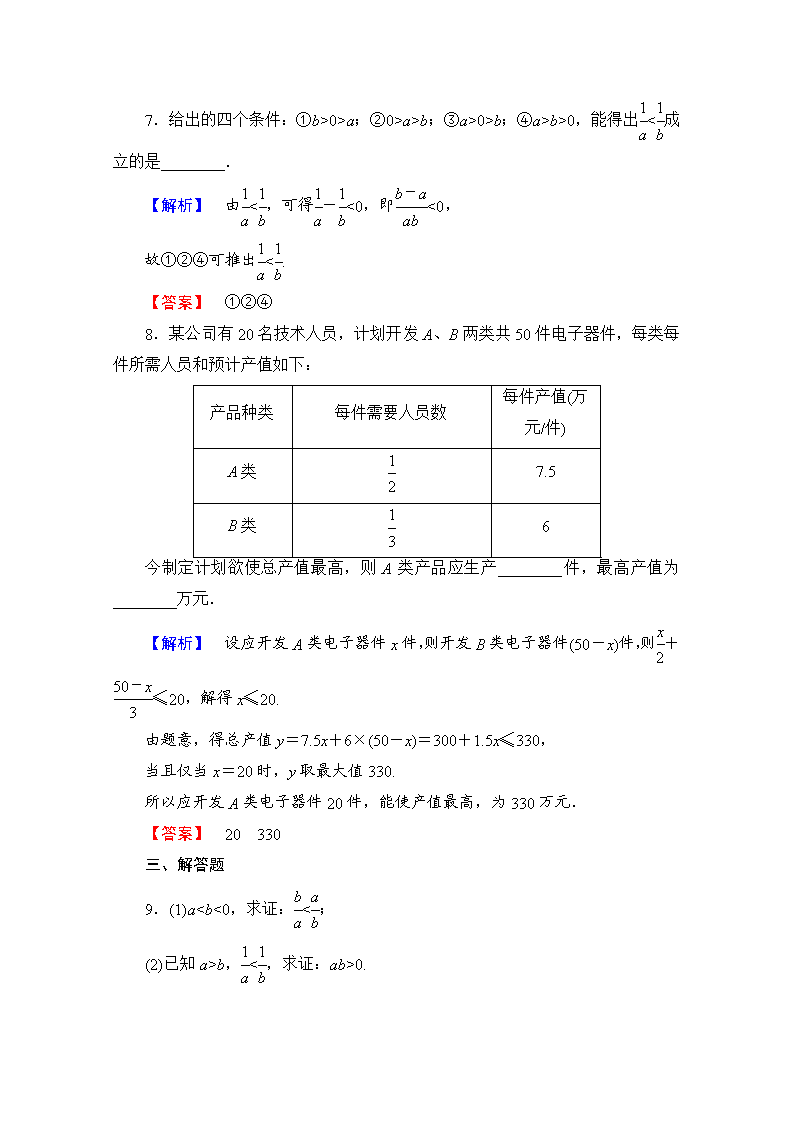
8.某公司有 20 名技术人员,计划开发 A、B 两类共 50 件电子器件,每类每
件所需人员和预计产值如下:
产品种类 每件需要人员数
每件产值(万
元/件)
A 类 1
2 7.5
B 类 1
3 6
今制定计划欲使总产值最高,则 A 类产品应生产________件,最高产值为
________万元.
【解析】 设应开发 A 类电子器件 x 件,则开发 B 类电子器件(50-x)件,则x
2
+50-x
3
≤20,解得 x≤20.
由题意,得总产值 y=7.5x+6×(50-x)=300+1.5x≤330,
当且仅当 x=20 时,y 取最大值 330.
所以应开发 A 类电子器件 20 件,能使产值最高,为 330 万元.
【答案】 20 330
三、解答题
9.(1)ab,1
a<1
b
,求证:ab>0.
【证明】 (1)由于b
a
-a
b
=b2-a2
ab
=b+ab-a
ab
,
∵a0,ab>0,
∴b+ab-a
ab <0,故b
ab,
∴b-a<0,
∴ab>0.
10.(1)已知 x<1,比较 x3-1 与 2x2-2x 的大小;
(2)已知 120,
∴(x-1)
x-1
2 2+3
4 <0,
∴x3-1<2x2-2x.
(2)∵15b>0,cb
d B.a
cb
c D.a
db>1,c<0,给出下列三个结论:①c
a>c
b
;②acloga(b
-c).其中所有的正确结论的序号是( )
A.① B.①②
C.②③ D.①②③
【解析】 由 a>b>1,得 0<1
a<1
b
,又 c<0,所以c
a>c
b
,①正确;幂函数 y=xc(c<0)
在(0,+∞)上是减函数,所以 acb-c>0,所以 logb(a-
c)>loga(a-c)>loga(b-c),③正确.故①②③均正确.
【答案】 D
3.(2016·福建泉州月考)若 x>y,a>b,则在①a-x>b-y;②a+x>b+y;③ax>by;
④x-b>y-a;⑤a
y>b
x
,这五个式子中,恒成立的所有不等式的序号是________. 【导
学号:05920074】
【解析】 令 x=-2,y=-3,a=3,b=2,符合题设条件 x>y,a>b.∵a-x
=3-(-2)=5,b-y=2-(-3)=5,∴a-x=b-y,因此①不成立;
又∵ax=-6,by=-6,∴ax=by,因此③也不成立;
又∵a
y
= 3
-3
=-1,b
x
= 2
-2
=-1,
∴a
y
=b
x
,因此⑤不成立.由不等式的性质可推出②④成立.
【答案】 ②④
4.某单位组织职工去某地参观学习需包车前往.甲车队说:“如领队买全票
一张,其余人可享受 7.5 折优惠”.乙车队说:“你们属团体票,按原价的 8 折优
惠.”这两车队的原价、车型都是一样的.试根据单位去的人数,比较两车队的
收费哪家更优惠.
【解】 设该单位有职工 n 人(n∈N*),全票价为 x 元,坐甲车需花 y1 元,坐
乙车需花 y2 元,
则 y1=x+3
4x(n-1)=1
4x+3
4xn,y2=4
5xn,
所以 y1-y2=1
4x+3
4xn-4
5xn=1
4x- 1
20xn
=1
4x 1-n
5 .
当 n=5 时,y1=y2;当 n>5 时,y1y2.
因此当单位人数为 5 时,两车队收费相同;多于 5 人时,选甲车队更优惠;
少于 5 人时,选乙车队更优惠.