- 2021-04-25 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
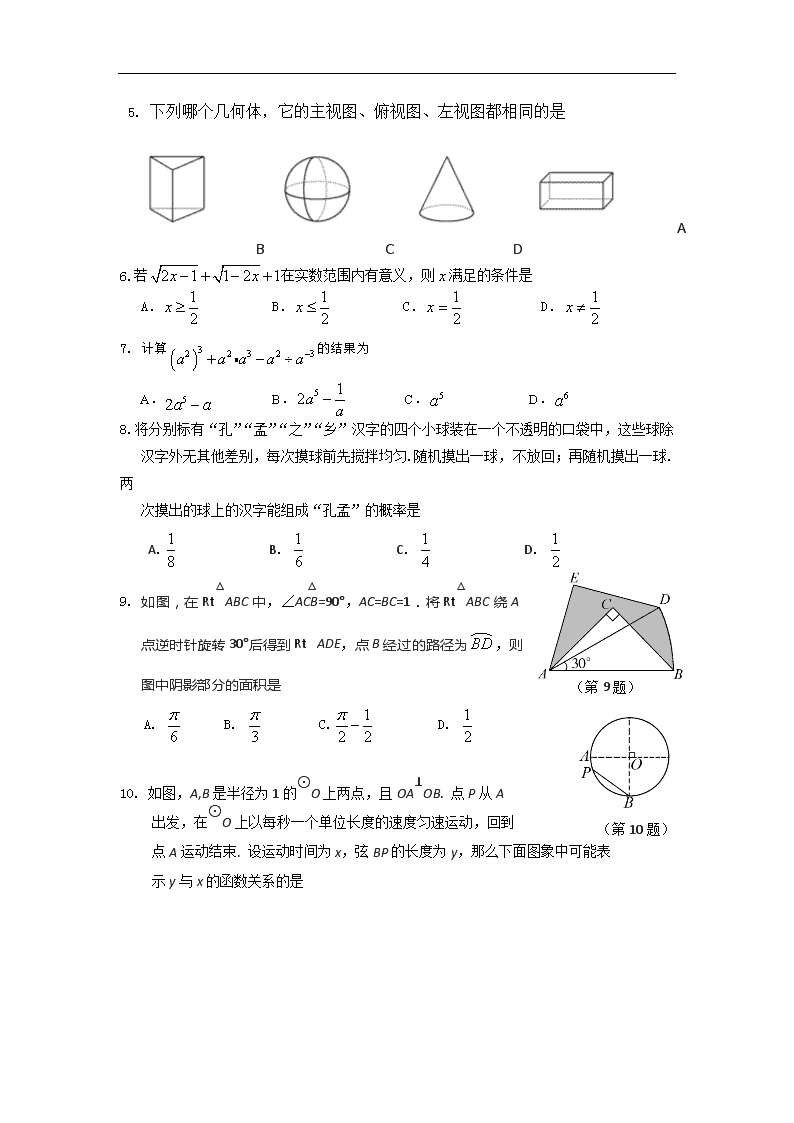
山东省济宁市2017年中考数学试题
济宁市二0一七年高中段学校招生考试 数 学 试 题 注意事项: 1.本试卷分第Ⅰ卷和第Ⅱ卷两部分,共6页.第Ⅰ卷为选择题,30分;第Ⅱ卷为非选择题,70分;共100分.考试时间为120分钟. 2.答题前,考生务必先核对条形码上的姓名、准考证号和座号,然后用0.5毫米黑色签字笔将本人的姓名、准考证号和座号填写在答题卡相应位置. 3.答第Ⅰ卷时,必须使用2B铅笔把答题卡上相应题目的答案标号(ABCD)涂黑,如需改动,必须先用橡皮擦干净,再改涂其它答案. 4.答第Ⅱ卷时,必须使用0.5毫米黑色签字笔在答题卡上书写.务必在题号所指示的答题区域内作答. 5.填空题请直接将答案填写在答题卡上,解答题应写出文字说明、证明过程或演算步骤. 6.考试结束后,将本试卷和答题卡一并交回. 第I卷(选择题 共30分) 一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求. 1.的倒数是 A. 6 B. C. D. 2. 单项式与是同类项,则的值是 A.2 B.3 C.4 D.5 3. 下列图形是中心对称图形的是 4.某桑蚕丝的直径约为0.000016米,将0.000016用科学记数法表示是 A. B. C. D. 5. 下列哪个几何体,它的主视图、俯视图、左视图都相同的是 A B C D 6.若在实数范围内有意义,则满足的条件是 A. B. C. D. 7. 计算的结果为 A. B. C. D. 8. 将分别标有“孔”“孟”“之”“乡”汉字的四个小球装在一个不透明的口袋中,这些球除 汉字外无其他差别,每次摸球前先搅拌均匀.随机摸出一球,不放回;再随机摸出一球.两 次摸出的球上的汉字能组成“孔孟”的概率是 A. B. C. D. (第9题) 9. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1.将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为,则图中阴影部分的面积是 A. B. C. D. 10. 如图,A,B是半径为1的⊙O上两点,且OA⊥OB. 点P从A (第10题) 出发,在⊙O上以每秒一个单位长度的速度匀速运动,回到 点A运动结束. 设运动时间为x,弦BP的长度为y,那么下面图象中可能表 示y与x的函数关系的是 A. ① B.④ C.②或④ D. ①或③ 第Ⅱ卷(选择题 共70分) 二、填空题:本大题共5小题,每小题3分,共15分. 11. 分解因式:= . 12. 请写出一个过(1,1),且与x轴无交点的函数表达式: . 13. 《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若 干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的,那 么乙也共有钱48文.甲,乙二人原来各有多少钱?” 设甲原有x文钱,乙原有y文钱,可列方程组为 . 14. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧, 交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN 的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(a,b), (第14题) 则a与b的数量关系为 . 15.如图,正六边形的边长为1,它的6条对角线又围成一个正六边形,如此继续下去,则六边形的面积是 . 三、解答题:本大题共7小题,共55分. (第15题) 16.(6分)解方程: 17.(6分)为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图: (第17题) (1)该班总人数是 ; (2)根据计算,请你补全两个统计图; (3)观察补全后的统计图,写出一条你发现的结论. 18.(7分)某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系: y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元. (1)求w与x之间的函数关系式; (2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元? (3)如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元? 19.(8分)如图,已知⊙O的直径AB=10,弦AC=8,D是 的中点,过点D作DE⊥AC交AC的延长线于点E. (1)求证:DE是⊙O的切线; (2)求AE的长. (第19题) 20.(8分)实验探究: (1)如图1,对折矩形纸片ABCD,使AD与BC重合, 得到折痕EF,把纸片展平;再一次折叠纸片,使点 图1 (第20题) A落在EF上,并使折痕经过点B,得到折痕BM, 同时得到线段BN,MN. 请你观察图1,猜想∠MBN的度数是多少,并证明你的结论. (2)将图1中的三角形纸片BMN剪下,如图2. 图2 (第20题) 折叠该纸片,探究MN与BM的数量关系.写出折叠方案, 并结合方案证明你的结论. 21.(9分)已知函数的图象与轴有两个公共点. (1)求的取值范围,写出当取范围内最大整数时函数的解析式; (2)题(1)中求得的函数记为C1 ①当时,的取值范围是,求的值; ②函数C2:的图象由函数C1的图象平移得到,其顶点P落在以原 点为圆心,半径为的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距 离最大时函数C2的解析式. 22.(11分)定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点. 例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点. 请你运用所学知识,结合上述材料,解决下列问题: (第22题) 在平面直角坐标系中,点M是曲线C:上的任意一点,点N是x轴正半轴上的任意一点. (1) 如图2,点P是OM上一点,∠ONP=∠M, 试说明点P是△MON的自相似点; 当点M的坐标是,点N的坐标是时,求点P 的坐标; (第22题) (2) 如图3,当点M的坐标是,点N的坐标是时,求△MON的自相似点的坐标; (3) 是否存在点M和点N,使△MON无自相似点,?若存在,请直接写出这两点的坐标;若不存在,请说明理由. 济宁市二○一七年高中段学校招生考试 数学试题参考答案及评分标准 说明:解答题各小题只给出了一种解法及评分标准.其他解法,只要步骤合理,解答正确,均应给出相应的分数. 一、选择题 (每小题3分,共30分) 题号 1 2 3 4 5 6 7 8 9 10 选项 A D C B B C D B A D 二、填空题(每小题3分,共15分) 11. ; 12. (答案不唯一); 13. ; 14. ; 15. . 三、解答题(共55分) 16.解:方程两边乘,得 .………………………………2分 解得 .…………………………………4分 检验:当时,.…………………………………………5分 所以原分式方程的解为. ………………………………………6分 17.解:(1) 40………………………………………………………………1分 (2) (每填对一图得2分) (3)答案不唯一,如优秀人数逐渐增多,增大的幅度逐渐减小等.……………6分 18.解:(1) 所以w与x的函数关系式为:(30≤x≤60)…………2分 (2). ………………………………3分 ∵﹣1<0, ∴当x=45时,w有最大值.w最大值为225.………………………………4分 答:销售单价定为45元时,每天销售利润最大,最大销售利润225元.……5分 (3)当w=200时,可得方程. 解得 x1=40,x2=50.………………………………………………………6分 ∵50>48, ∴x2=50不符合题意,应舍去. 答:该商店销售这种健身球每天想要获得200元的销售利润,销售单价应定为40元. ……………………………………………………………7分 19.证明:(1)连接OD, ∵D是的中点,∴ ∴ ∴OD∥AE, ∵DE⊥AC,∴∴ ∴OD⊥DE. ∴DE是⊙O 的切线.……………………………………………………………4分 (2)过点O作OF⊥AC于点F,∵ ∴ ∵∠OFE=∠DEF=∠ODE=90°, ∴四边形OFED是矩形, ∴FE=OD=.∵,∴FE=6 ∴AE=AF+FE=5+6=11.……………………………………………………… 8分 20. 解:(1)………………………………………………………… 1分 证明:连接AN, ∵直线EF是AB的垂直平分线,点N在EF上, ∴AN=BN. 由折叠可知,BN=AB, ∴△ABN是等边三角形. ∴. ∴.…………………………… 3分 (2)………………………………………………………………… 4分 折纸方案:如图,折叠三角形纸片BMN,使点N落在BM上,并使折痕经过点M,得到折痕MP,同时得到线段PO. …………………………………………………………… 6分 证明:由折叠知, ∴ ∴ ∵,∴ ∴.∴ ∴ …………………………………………………………8分 21. 解:(1)由题意可得:解得:且 当时,函数解析式为:.……………………… 3分 (2)函数图象开口向上,对称轴为 ∴当时,随的增大而减小. ∵当时,的取值范围是, ∴ . ∴ 或(舍去). ∴ .……………………………………………………… 6分 (3)∵ ∴图象顶点的坐标为, 由图形可知当为射线与圆的交点时,距离最大. ∵点P在直线OM上,由可求得直线解析式为:, 设P(a,b),则有a=2b, 根据勾股定理可得 求得. ∴PM最大时的函数解析式为.…………………………… 9分 22.解:(1)在△ONP和△OMN中, ∵∠ONP=∠OMN,∠NOP=∠MON ∴△ONP∽△OMN 图1 ∴点P是△M0N的自相似点.……………………………………………………… 2分 过点P作PD⊥x轴于D点. ∴. ∵, ∴, ∴. 在Rt△中,. . . ∴.……………………… 4分 (2) ①如图2,过点M作MH⊥x轴于H点, ∵ , ∴,直线OM的表达式为. ∵是△M0N的自相似点,∴△∽△NOM 过点作⊥x轴于Q点, ∴ ∵的横坐标为1,∴ ∴. -------------------6分 如图3,△∽△NOM , 图3 ∴ ∴ . ∵的纵坐标为, ∴ ∴, ∴. 综上所述,或.-------------------------------------------------------9分 (3)存在,.-------------------------------------------------------------11分查看更多