中考数学难度适中题一

中考数学难度适中题一

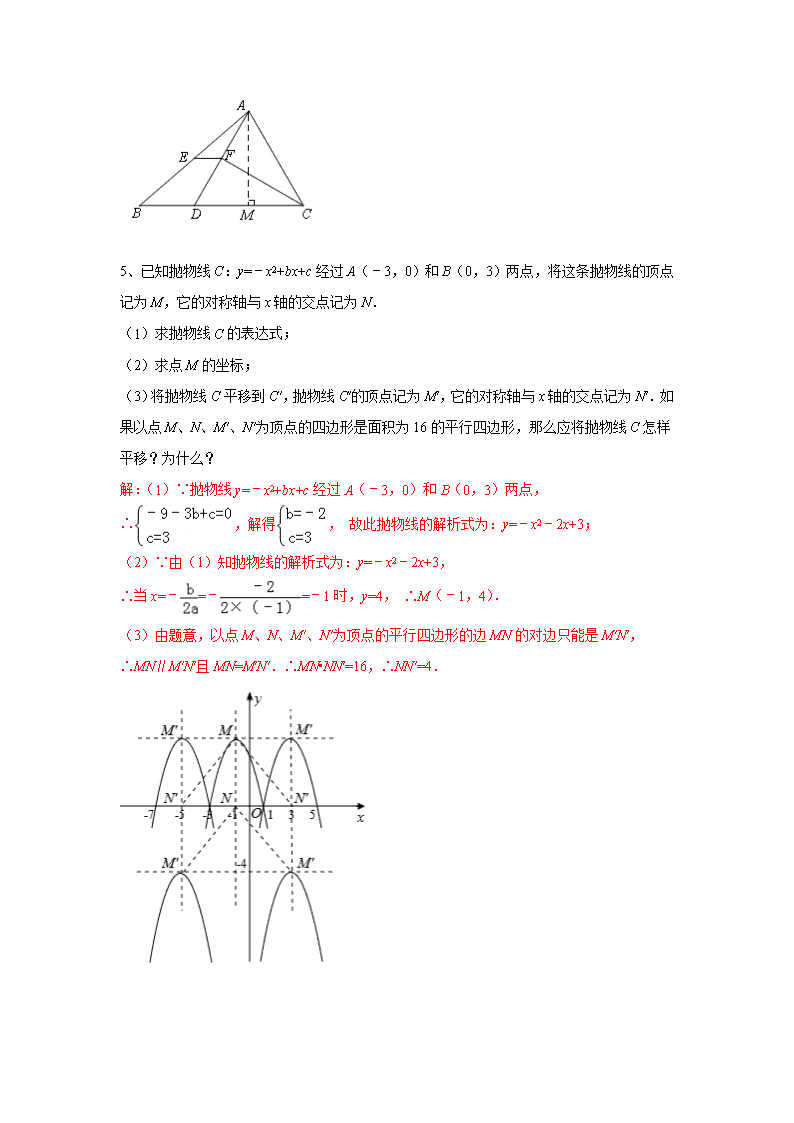
中考数学难度适中题（一）‎ ‎1、如图，已知AB为⊙O的直径，∠E=20°，∠DBC=50°，求∠CBE的度数．‎ ‎ ‎ 解：连接AC，∵，∴∠DBA=∠DCA，‎ ‎∵AB为⊙O的直径，∴∠BCA=90°，∴∠CBA+∠CAB=90°，‎ ‎∵∠CAB=∠E+∠DCA，∴∠CBD+∠DBA+∠E+∠DBA=90°，‎ ‎∵∠E=20°，∠DBC=50°，∴∠DBA=10°，‎ ‎∴∠CBE=∠DBA+∠CBD=10°+50°=60°． ‎ ‎2、如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠AMB=45°，则四边形MANB面积的最大值是　4　．‎ ‎ ‎ ‎ 解：过点O作OC⊥AB于C，交⊙O于D、E两点，连结OA、OB、DA、DB、EA、EB，如图，∵∠AMB=45°，∴∠AOB=2∠AMB=90°，∴△OAB为等腰直角三角形，‎ ‎∴AB=OA=2， ∵S四边形MANB=S△MAB+S△NAB，‎ ‎∴当M点到AB的距离最大，△MAB的面积最大；当N点到AB的距离最大时，△NAB的面积最大，即M点运动到D点，N点运动到E点，‎ 此时四边形MANB面积的最大值=S四边形DAEB=S△DAB+S△EAB=AB•CD+AB•CE=AB（CD+CE）=AB•DE=×2×4=4．故答案为4．‎ ‎3、如图，⊙O的半径为4，B是⊙O外一点，连接OB，且OB=6，过点B作⊙O的切线BD，切点为D，延长BO交⊙O于点A，过点A作切线BD的垂线，垂足为C．‎ ‎（1）求证：AD平分∠BAC；‎ ‎（2）求AC的长．‎ ‎（1）证明：连接OD，‎ ‎∵BD是⊙O的切线，∴OD⊥BD，‎ ‎∵AC⊥BD，OD∥AC，∴∠2=∠3，‎ ‎∵OA=OD，∴∠1=∠3，∴∠1=∠2，即AD平分∠BAC；‎ ‎（2）解：∵OD∥AC，∴△BOD∽△BAC，‎ ‎∴，∴，解得：AC=．‎ ‎4、如图，△ABC中，BC >AC，点D在BC上，且CA=CD，∠ACB的平分线交AD于点F，E是AB的中点．‎ ‎（1）求证：EF∥BD ；‎ ‎（2）若∠ACB=60°，AC=8，BC=12，求四边形BDFE的面积．‎ 试题分析：（1）由题意可推出△ADC为等腰三角形，CF为顶角的角平分线，所以也是底边上的中线和高，因此F为AD的中点，所以EF为△ABD的中位线，即EF∥BD.‎ ‎（2）根据（1）的结论，可以推出△AEF∽△ABD，且S△AEF：S△ABD=1：4，所以S△AEF：S四边形BDEF=1：3，即可求出△AEF的面积，从而由求得四边形BDFE的面积．‎ ‎（1）∵ CA=CD，CF平分∠ACB，∴ CF是AD边的中线．‎ ‎∵ E是AB的中点，∴ EF是△ABD的中位线．‎ ‎∴ EF∥BD .‎ ‎（2）∵∠ACB=60°，CA=CD，∴△CAD是等边三角形．‎ ‎∴∠ADC=60°，AD=DC=AC=8．∴ BD=BC-CD=4．‎ 如图，过点A作AM⊥BC，垂足为M ．‎ ‎∴．．‎ ‎∵ EF∥BD ，∴△AEF ∽△ABD ，且．‎ ‎∴．∴． ‎ 四边形BDFE的面积=．‎ ‎5、已知抛物线C：y=﹣x2+bx+c经过A（﹣3，0）和B（0，3）两点，将这条抛物线的顶点记为M，它的对称轴与x轴的交点记为N．‎ ‎（1）求抛物线C的表达式；‎ ‎（2）求点M的坐标；‎ ‎（3）将抛物线C平移到C′，抛物线C′的顶点记为M′，它的对称轴与x轴的交点记为N′．如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形，那么应将抛物线C怎样平移？为什么？‎ 解：（1）∵抛物线y=﹣x2+bx+c经过A（﹣3，0）和B（0，3）两点，‎ ‎∴，解得， 故此抛物线的解析式为：y=﹣x2﹣2x+3；‎ ‎（2）∵由（1）知抛物线的解析式为：y=﹣x2﹣2x+3，‎ ‎∴当x=﹣=﹣=﹣1时，y=4， ∴M（﹣1，4）．‎ ‎（3）由题意，以点M、N、M′、N′为顶点的平行四边形的边MN的对边只能是M′N′，‎ ‎∴MN∥M′N′且MN=M′N′．∴MN•NN′=16，∴NN′=4．‎ i）当M、N、M′、N′为顶点的平行四边形是▱MNN′M′时，将抛物线C向左或向右平移4个单位可得符合条件的抛物线C′；‎ ii）当M、N、M′、N′为顶点的平行四边形是▱MNM′N′时，将抛物线C先向左或向右平移4个单位，再向下平移8个单位，可得符合条件的抛物线C′．‎ ‎∴上述的四种平移，均可得到符合条件的抛物线C′．‎ ‎6、问题探究 ‎（1）如图①，在矩形ABCD中，AB=3，BC=4，如果BC边上存在点P，使△APD为等腰三角形，那么请画出满足条件的一个等腰三角形△APD，并求出此时BP的长；‎ ‎ ‎ ‎（1）①作AD的垂直平分线交BC于点P，如图①，则PA=PD．∴△PAD是等腰三角形．‎ ‎∵四边形ABCD是矩形，∴AB=DC，∠B=∠C=90°．‎ ‎∵PA=PD，AB=DC，∴Rt△ABP≌Rt△DCP（HL）．∴BP=CP．‎ ‎∵BC=4，∴BP=CP=2．‎ ‎②以点D为圆心，AD为半径画弧，交BC于点P′，如图①，．则DA=DP′．‎ ‎∴△P′AD是等腰三角形．∵四边形ABCD是矩形，∴AD=BC，AB=DC，∠C=90°．‎ ‎∵AB=3，BC=4，∴DC=3，DP′=4．∴CP′==．∴BP′=4﹣．‎ ‎③点A为圆心，AD为半径画弧，交BC于点P″，如图①，则AD=AP″．‎ ‎∴△P″AD是等腰三角形．同理可得：BP″=．‎ 综上所述：在等腰三角形△ADP中，‎ 若PA=PD，则BP=2；若DP=DA，则BP=4﹣；若AP=AD，则BP=．‎ ‎（2）如图②，在△ABC中，∠ABC=60°，BC=12，AD是BC边上的高，E、F分别为边AB、AC的中点，当AD=6时，BC边上存在一点Q，使∠EQF=90°，求此时BQ的长；‎ 问题解决 ‎ ‎ ‎（2）∵E、F分别为边AB、AC的中点，∴EF∥BC，EF=BC．‎ ‎∵BC=12，∴EF=6．‎ 以EF为直径作⊙O，过点O作OQ⊥BC，垂足为Q，连接EQ、FQ，如图②．‎ ‎∵AD⊥BC，AD=6，∴EF与BC之间的距离为3．‎ ‎∴OQ=3 ∴OQ=OE=3．∴⊙O与BC相切，切点为Q．‎ ‎∵EF为⊙O的直径，∴∠EQF=90°．‎ 过点E作EG⊥BC，垂足为G，如图②．‎ ‎∵EG⊥BC，OQ⊥BC，∴EG∥OQ．‎ ‎∵EO∥GQ，EG∥OQ，∠EGQ=90°，OE=OQ，∴四边形OEGQ是正方形．‎ ‎∴GQ=EO=3，EG=OQ=3．‎ ‎∵∠B=60°，∠EGB=90°，EG=3，∴BG=．∴BQ=GQ+BG=3+．‎ ‎∴当∠EQF=90°时，BQ的长为3+．‎ ‎（3）有一山庄，它的平面图为如图③的五边形ABCDE，山庄保卫人员想在线段CD上选一点M安装监控装置，用来监视边AB，现只要使∠AMB大约为60°，就可以让监控装置的效果达到最佳，已知∠A=∠E=∠D=90°，AB=270m，AE=400m，ED=285m，CD=340m，问在线段CD上是否存在点M，使∠AMB=60°？若存在，请求出符合条件的DM的长，若不存在，请说明理由．‎ ‎ ‎ 解：（3）在线段CD上存在点M，使∠AMB=60°．‎ 理由如下：‎ 以AB为边，在AB的右侧作等边三角形ABG，‎ 作GP⊥AB，垂足为P，作AK⊥BG，垂足为K．‎ 设GP与AK交于点O，以点O为圆心，OA为半径作⊙O，‎ 过点O作OH⊥CD，垂足为H，如图③．则⊙O是△ABG的外接圆，‎ ‎∵△ABG是等边三角形，GP⊥AB，∴AP=PB=AB．‎ ‎∵AB=270，∴AP=135．∵ED=285，∴OH=285﹣135=150．‎ ‎∵△ABG是等边三角形，AK⊥BG，∴∠BAK=∠GAK=30°．‎ ‎∴OP=AP•tan30°=135×=45．∴OA=2OP=90．∴OH＜OA．‎ ‎∴⊙O与CD相交，设交点为M，连接MA、MB，如图③．‎ ‎∴∠AMB=∠AGB=60°，OM=OA=90．‎ ‎∵OH⊥CD，OH=150，OM=90，∴HM===30．‎ ‎∵AE=400，OP=45，∴DH=400﹣45．‎ 若点M在点H的左边，则DM=DH+HM=400﹣45+30．‎ ‎∵400﹣45+30＞340，∴DM＞CD． ‎ ‎∴点M不在线段CD上，应舍去． ‎ 若点M在点H的右边，则DM=DH﹣HM=400﹣45﹣30．‎ ‎∵400﹣45﹣30＜340，∴DM＜CD．∴点M在线段CD上．‎ 综上所述：在线段CD上存在唯一的点M，使∠AMB=60°，‎ 此时DM的长为（400﹣45﹣30）米．‎