统计高考真题

统计高考真题

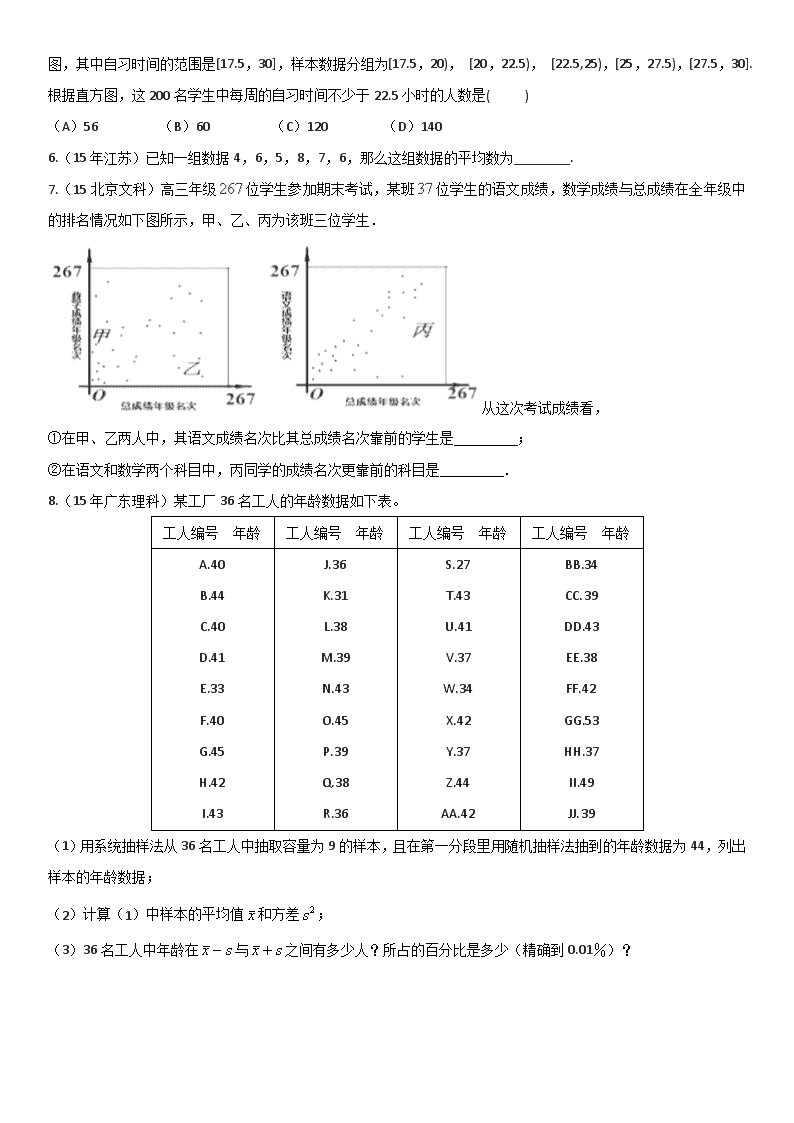
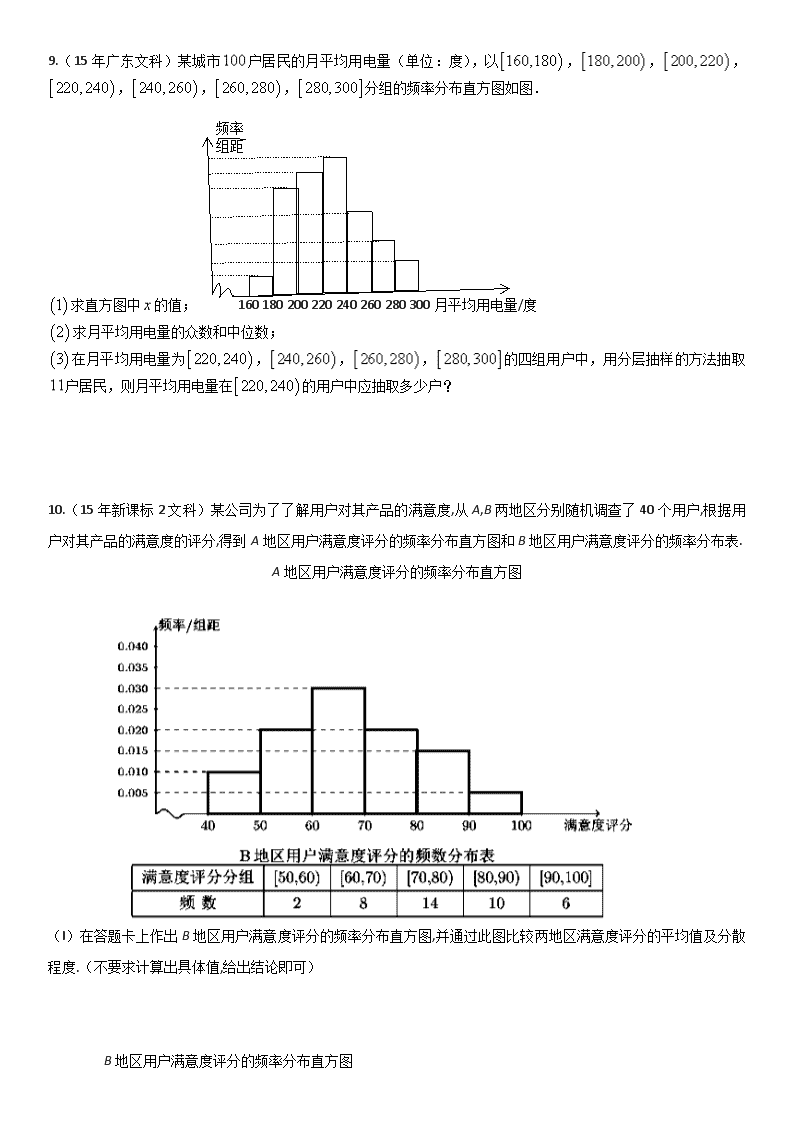
统计测试 ‎1.（15北京文科）某辆汽车每次加油都把油箱加满，下表记录了该车相邻两次加油时的情况．‎ 加油时间 加油量（升）‎ 加油时的累计里程（千米）‎ 年月日 年月日 注：“累计里程“指汽车从出厂开始累计行驶的路程，在这段时间内，该车每千米平均耗油量为（ ）‎ A．升 B．升 C．升 D．升 ‎2.（15年湖南理科）在一次马拉松比赛中，35名运动员的成绩（单位：分钟）的茎叶图如图4所示.‎ 若将运动员按成绩由好到差编为号，再用系统抽样方法从中抽取7人，则其中成绩在区间[139,151]上的运动员人数是 .‎ ‎13 0 0 3 4 5 6 6 8 8 8 9‎ ‎14 1 1 1 2 2 2 3 3 4 4 5 5 5 6 6 7 8‎ ‎15 0 1 2 2 3 3 3‎ ‎3.（15年陕西文科）某中学初中部共有110名教师，高中部共有150名教师，其性别比例如图所示，则该校女教师的人数为（ ）‎ A．93 B．123 C．137 D．167‎ ‎4.（15年福建理科）为了解某社区居民的家庭年收入所年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：‎ 收入 （万元）‎ ‎8.2‎ ‎8.6‎ ‎10.0‎ ‎11.3‎ ‎11.9‎ 支出 （万元）‎ ‎6.2‎ ‎7.5‎ ‎8.0‎ ‎8.5‎ ‎9.8‎ 根据上表可得回归直线方程 ，其中 ，据此估计，该社区一户收入为15万元家庭年支出为( )]‎ A．11.4万元 B．11.8万元 C．12.0万元 D．12.2万元 ‎ 频率 ‎ 组距 ‎ ‎17.5 20 22.5 25 27.5 30 自习时间 ‎ ‎5.（2016·山东高考）‎ 某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20)， [20，22.5)， [22.5,25)，[25，27.5)，[27.5，30].根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是( )‎ ‎（A）56 （B）60 （C）120 （D）140 ‎ ‎6.（15年江苏）已知一组数据4，6，5，8，7，6，那么这组数据的平均数为________.‎ ‎7.（15北京文科）高三年级位学生参加期末考试，某班位学生的语文成绩，数学成绩与总成绩在全年级中的排名情况如下图所示，甲、乙、丙为该班三位学生．‎ 从这次考试成绩看，‎ ‎①在甲、乙两人中，其语文成绩名次比其总成绩名次靠前的学生是 ；‎ ‎②在语文和数学两个科目中，丙同学的成绩名次更靠前的科目是 ．‎ ‎8.（15年广东理科）某工厂36名工人的年龄数据如下表。‎ 工人编号 年龄 工人编号 年龄 工人编号 年龄 工人编号 年龄 A. ‎40‎ B. ‎44‎ C. ‎40‎ D. ‎41‎ E. ‎33‎ F. ‎40‎ G. ‎45‎ H. ‎42‎ I. ‎43‎ J. ‎36‎ K. ‎31‎ L. ‎38‎ M. ‎39‎ N. ‎43‎ O. ‎45‎ P. ‎39‎ Q. ‎38‎ R. ‎36‎ S. ‎27‎ T. ‎43‎ U. ‎41‎ V. ‎37‎ W. ‎34‎ X. ‎42‎ Y. ‎37‎ Z. ‎44‎ AA. ‎42‎ BB. ‎34‎ CC. ‎39‎ DD. ‎43‎ EE. ‎38‎ FF. ‎42‎ GG. ‎53‎ HH. ‎37‎ II. ‎49‎ JJ. ‎39‎ ‎（1）用系统抽样法从36名工人中抽取容量为9的样本，且在第一分段里用随机抽样法抽到的年龄数据为44，列出样本的年龄数据；‎ ‎（2）计算（1）中样本的平均值和方差；‎ ‎（3）36名工人中年龄在与之间有多少人？所占的百分比是多少（精确到0.01％）？‎ ‎9.（15年广东文科）某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．‎ ‎ ‎ ‎ 频率 ‎ 组距 ‎ ‎ 求直方图中的值； 160 180 200 220 240 260 280 300月平均用电量/度 求月平均用电量的众数和中位数；‎ 在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？‎ ‎10.（15年新课标2文科）某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.‎ A地区用户满意度评分的频率分布直方图 ‎（I）在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.（不要求计算出具体值,给出结论即可）‎ B地区用户满意度评分的频率分布直方图 ‎（II）根据用户满意度评分,将用户的满意度评分分为三个等级：‎ 估计那个地区的用户的满意度等级为不满意的概率大,说明理由.‎ ‎11.（2016·全国新课标III）下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.‎ 注：年份代码1–7分别对应年份2008–2014.‎ ‎（Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；‎ ‎（Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.‎ 附注：参考数据：，，，≈2.646.参考公式：回归方程中斜率和截距的最小二乘估计公式分别为：‎ ‎12.（2016·四川高考）我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超出 的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5)，[0.5,1)，…，[4,4.5)分成9组，制成了如图所示的频率分布直方图.‎ ‎（I）求直方图中a的值；‎ ‎（II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；‎ ‎（III）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由.‎ ‎13. （2017年全国Ⅱ卷理）海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100 个网箱，测量各箱水产品的产量（单位：kg）某频率分布直方图如下：‎ ‎ ‎ 设两种养殖方法的箱产量相互独立，记A表示事件：“旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg”，估计A的概率；‎ 填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关： 附：‎ 箱产量＜50kg 箱产量≥50kg 旧养殖法 新养殖法 根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到0.01） ‎ ‎1.【答案】B 2.【答案】.3.【答案】4.【答案】B 考点：线性回归方程．5.【解析】选D。由频率分布直方图可知，每周自习时间不少于22.5小时的学生所占频率为：，所以每周自习时间不少于22.5小时的学生人数为：‎ ‎6.【答案】6‎ ‎7.【答案】乙、数学 ‎【解析】‎ 试题分析：①由图可知，甲的语文成绩排名比总成绩排名靠后；而乙的语文成绩排名比总成绩排名靠前，故填乙.‎ ‎②由图可知，比丙的数学成绩排名还靠后的人比较多；而总成绩的排名中比丙排名靠后的人数比较少，所以丙的数学成绩的排名更靠前，故填数学.‎ ‎8.【答案】（1），，，，，，，，；（2），；（3），约占．‎ ‎9.【答案】（1）；（2），；（3）．‎ ‎【解析】‎ ‎11.解：（Ⅰ）由折线图中的数据和附注中参考数据得 因为与的相关系数近似为，说明与的线性相关程度相当高，从而可以用线性回归模型拟合与的关系.‎ ‎（Ⅱ）由及得，‎ 所以，与的回归方程为 将2016年对应的代入回归方程得：‎ 所以预测2016年我国生活垃圾无害化处理量将约为1.82亿吨.‎ ‎12.【解析】（I）由概率统计相关知识，各组频率之和的值为1，因为频率=(频率/组距)*组距，所以，得 ‎（II）由图，不低于3吨人数所占百分比为，所 以全市月均用水量不低于3吨的人数为：(万)‎ ‎（III）由图可知，月均用水量小于2.5吨的居民人数所占百分比为：‎ ‎，即的居民月均用水量小于2.5吨,同理，88%的居民月均用水量小于3吨，故，假设月均用水量平均分布，则（吨）.‎