- 2021-04-25 发布 |
- 37.5 KB |
- 7页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学第7章(第12课时)简单的线性规划2
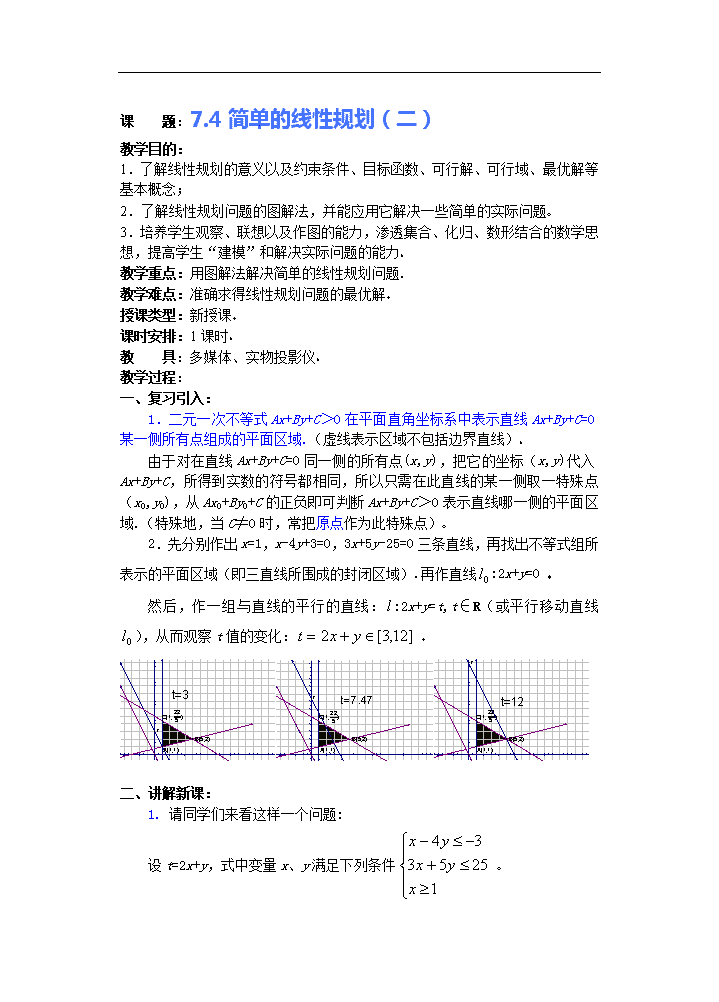
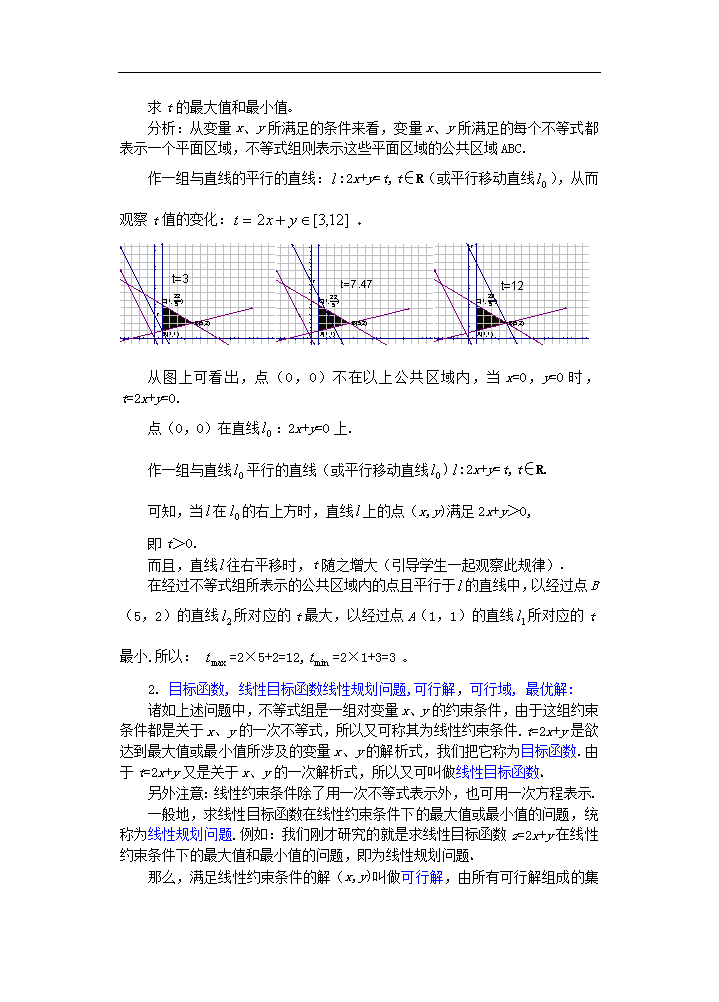
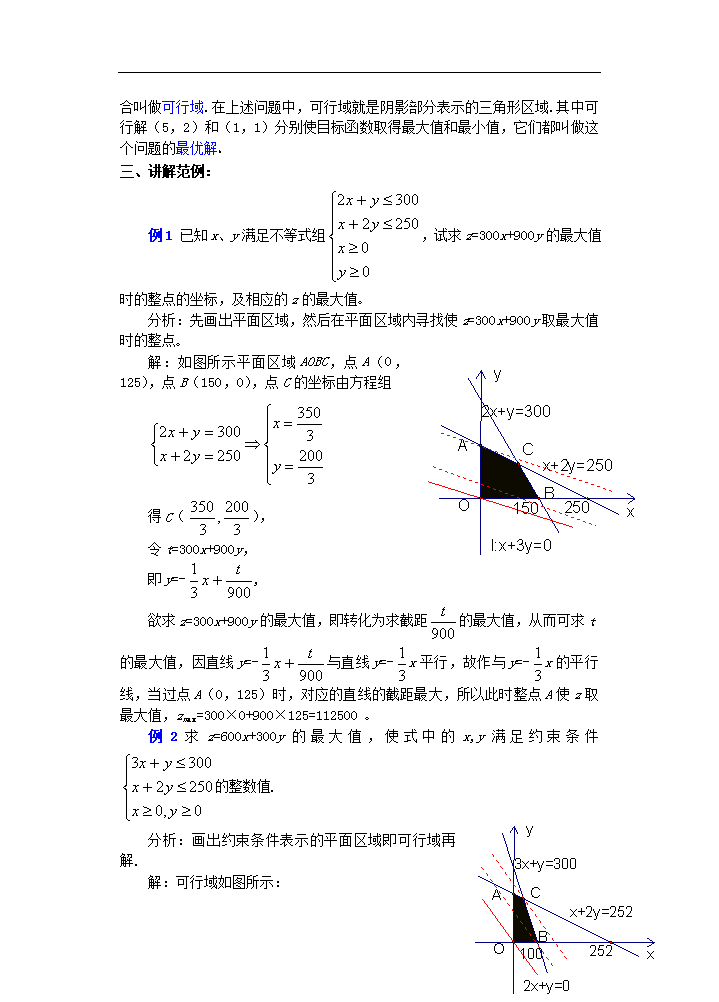
课 题:7.4简单的线性规划(二) 教学目的: 1.了解线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念; 2.了解线性规划问题的图解法,并能应用它解决一些简单的实际问题 3.培养学生观察、联想以及作图的能力,渗透集合、化归、数形结合的数学思想,提高学生“建模”和解决实际问题的能力 教学重点:用图解法解决简单的线性规划问题. 教学难点:准确求得线性规划问题的最优解 授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 教学过程: 一、复习引入: 1.二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线) 由于对在直线Ax+By+C=0同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点) 2.先分别作出x=1,x-4y+3=0,3x+5y-25=0三条直线,再找出不等式组所表示的平面区域(即三直线所围成的封闭区域).再作直线:2x+y=0 然后,作一组与直线的平行的直线::2x+y=t,t∈R(或平行移动直线),从而观察t值的变化: 二、讲解新课: 1. 请同学们来看这样一个问题: 设t=2x+y,式中变量x、y满足下列条件 求t的最大值和最小值 分析:从变量x、y所满足的条件来看,变量x、y所满足的每个不等式都表示一个平面区域,不等式组则表示这些平面区域的公共区域ABC. 作一组与直线的平行的直线::2x+y=t,t∈R(或平行移动直线),从而观察t值的变化: 从图上可看出,点(0,0)不在以上公共区域内,当x=0,y=0时,t=2x+y=0. 点(0,0)在直线:2x+y=0上. 作一组与直线平行的直线(或平行移动直线):2x+y=t,t∈R. 可知,当在的右上方时,直线上的点(x,y)满足2x+y>0, 即t>0. 而且,直线往右平移时,t随之增大(引导学生一起观察此规律). 在经过不等式组所表示的公共区域内的点且平行于的直线中,以经过点B(5,2)的直线所对应的t最大,以经过点A(1,1)的直线所对应的t最小.所以: =2×5+2=12,=2×1+3=3 2. 目标函数, 线性目标函数线性规划问题,可行解,可行域, 最优解: 诸如上述问题中,不等式组是一组对变量x、y的约束条件,由于这组约束条件都是关于x、y的一次不等式,所以又可称其为线性约束条件.t=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,我们把它称为目标函数.由于t=2x+y又是关于x、y的一次解析式,所以又可叫做线性目标函数 另外注意:线性约束条件除了用一次不等式表示外,也可用一次方程表示. 一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.例如:我们刚才研究的就是求线性目标函数z=2x+y在线性约束条件下的最大值和最小值的问题,即为线性规划问题 那么,满足线性约束条件的解(x,y)叫做可行解 ,由所有可行解组成的集合叫做可行域.在上述问题中,可行域就是阴影部分表示的三角形区域.其中可行解(5,2)和(1,1)分别使目标函数取得最大值和最小值,它们都叫做这个问题的最优解 三、讲解范例: 例1 已知x、y满足不等式组,试求z=300x+900y的最大值时的整点的坐标,及相应的z的最大值 分析:先画出平面区域,然后在平面区域内寻找使z=300x+900y取最大值时的整点 解:如图所示平面区域AOBC,点A(0,125),点B(150,0),点C的坐标由方程组 得C(), 令t=300x+900y, 即y=-, 欲求z=300x+900y的最大值,即转化为求截距的最大值,从而可求t的最大值,因直线y=-与直线y=-x平行,故作与y=-x的平行线,当过点A(0,125)时,对应的直线的截距最大,所以此时整点A使z取最大值,zmax=300×0+900×125=112500 例2求z=600x+300y的最大值,使式中的x,y满足约束条件的整数值. 分析:画出约束条件表示的平面区域即可行域再解. 解:可行域如图所示: 四边形AOBC,易求点A(0,126),B(100,0)由方程组: 得点C的坐标为(69,91) 因题设条件要求整点(x,y)使z=600x+300y取最大值,将点(69,91),(70,90)代入z=600x+300y,可知当时,z取最大值为zmax=600×70+300×900=69000 例3 已知x、y满足不等式,求z=3x+y的最小值 分析:可先找出可行域,平行移动直线l0:3x+y=0,找出可行解,进而求出目标函数的最小值 解:不等式x+2y≥2,表示直线x+2y=2上及右上方的点的集合; 不等式2x+y≥1表示直线2x+y=1上及右上方的点的集合. 可行域如图所示: 作直线:3x+y=0,作一组与直线平行的直线:3x+y=t,(t∈R) ∵x、y是上面不等式组表示的区域内的点的坐标. 由图可知: 当直线:3x+y=t通过P(0,1)时,t取到最小值1,即zmin=1. 评述:简单线性规划问题就是求线性目标函数在线性约束条件下的最优解,无论此类题目是以什么实际问题提出,其求解的格式与步骤是不变的: (1)寻找线性约束条件,线性目标函数; (2)由二元一次不等式表示的平面区域做出可行域; (3)在可行域内求目标函数的最优解 四、课堂练习: 1.请同学们结合课本P64练习1来掌握图解法解决简单的线性规划问题. (1)求z=2x+y的最大值,使式中的x、y 满足约束条件 解:不等式组表示的平面区域如图所示: 当x=0,y=0时,z=2x+y=0 点(0,0)在直线:2x+y=0上. 作一组与直线平行的直线 :2x+y=t,t∈R. 可知,在经过不等式组所表示的公共区域内的点且平行于的直线中,以经过点A(2,-1)的直线所对应的t最大. 所以zmax=2×2-1=3. (2)求z=3x+5y的最大值和最小值,使式中的x、y满足约束条件 解:不等式组所表示的平面区域如图所示: 从图示可知,直线3x+5y=t在经过不等式组所表示的公共区域内的点时,以经过点(-2,-1)的直线所对应的t最小,以经过点()的直线所对应的t最大. 所以zmin=3×(-2)+5×(-1)=-11. zmax=3×+5×=14 五、小结 :用图解法解决简单的线性规划问题的基本步骤: 1.首先,要根据线性约束条件画出可行域(即画出不等式组所表示的公共区域); 2.设t=0,画出直线 3.观察、分析,平移直线,从而找到最优解 4.最后求得目标函数的最大值及最小值 六、课后作业: 1.某工厂用两种不同原料均可生产同一产品,若采用甲种原料,每吨成本1000元,运费500元,可得产品90千克;若采用乙种原料,每吨成本为1500元,运费400元,可得产品100千克,如果每月原料的总成本不超过6000元,运费不超过2000元,那么此工厂每月最多可生产多少千克产品? 分析:将已知数据列成下表 甲原料(吨) 乙原料(吨) 费用限额 成本 1000 1500 6000 运费 500 400 2000 产品 90 100 解:设此工厂每月甲、乙两种原料各x吨、y吨,生产z千克产品,则: z=90x+100y 作出以上不等式组所表示的平面区域,即可行域: 由 令90x+100y=t,作直线:90x+100y=0即9x+10y=0的平行线90x+100y=t,当90x+100y=t过点M()时,直线90x+100y=t中的截距最大. 由此得出t的值也最大,最大值zmax=90×=440. 答:工厂每月生产440千克产品. 2.某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大? 解:设每天生产A型桌子x张,B型桌子y张 则 目标函数为:z=2x+3y 作出可行域: 把直线:2x+3y=0向右上方平移至的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=2x+3y取最大值 解方程得M的坐标为(2,3). 答:每天应生产A型桌子2张,B型桌子3张才能获得最大利润 七、板书设计(略) 八、课后记: 查看更多