中考数学专题复习统计和概率同步练习二

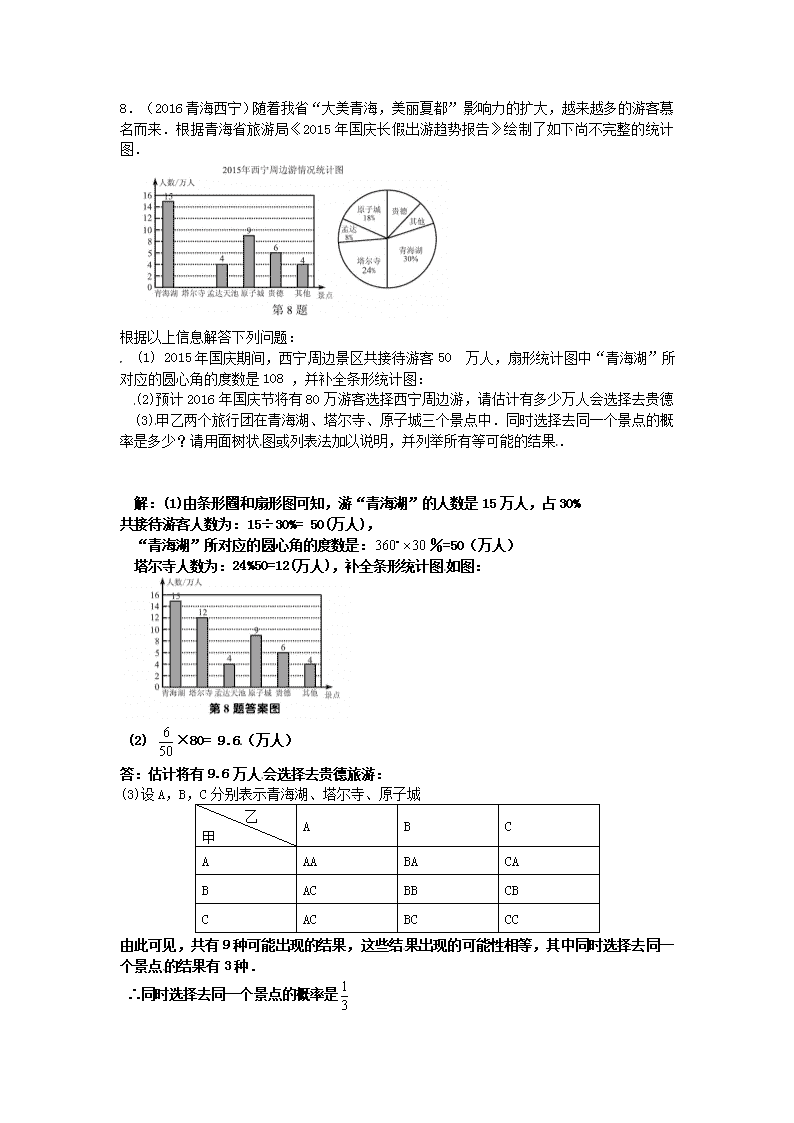
中考数学专题复习统计和概率同步练习二

‎《统计和概率》‎ 一、选择题 ‎1．（2016重庆育才）下列说法正确的是 (D)‎ A．必然事件发生的概率为0‎ B．明天下雨的概率是99%，说明明天一定会下雨 C．“面积相等的两个三角形全等”这一事件是必然事件 D．“任意一个三角形的外角和等于'’这一事件是不可能事件 ‎2．（2015山东泰安）如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是 (B)‎ ‎ A. B C. D. ‎ ‎3．一个不透明的袋子中有2个白球．3个黄球和1个红球，这些球除颜色不同外其他完全相同，则从袋子中随机摸出一个球是白球的概率为 ( C)‎ A. B. C. D. ‎ ‎4．让图中两个转盘分别白由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则两个数的和是2的倍数或3的倍数的概率等于 (C A. B. C. D. ‎ 二、填空 ‎5．（2016重庆八中）从-3，-2，-1，0，1，2这六个数字中随机抽取一个数，记为a，a，。的值既使得不等式组无解，又在函数的自变量取值范围内的概率是 ‎ ‎6．（2016重庆一中）抛一枚质地均匀各面分别刻有l、2、3、4、5、6点的正方体骰子，将所得的点数作为m的值，代人关于x，y的二元一次方程中，则此二元一次方程组有整数解的概率为 ‎7．（2016重庆育才）从2，1，0，-1，-3这五个数中，随机抽取一个数，作为正比例函数和关于x的方程中的m值,恰好使的所得的正比 例函数的图象经过第一、三象限，且方程有实数根的概率·‎ 三、解答题 ‎8．（2016青海西宁）随着我省“大美青海，美丽夏都”影响力的扩大，越来越多的游客慕名而来．根据青海省旅游局《2015年国庆长假出游趋势报告》绘制了如下尚不完整的统计图．‎ ‎ ‎ 根据以上信息解答下列问题：‎ ‎ (1) 2015年国庆期间，西宁周边景区共接待游客50 万人，扇形统计图中“青海湖”所对应的圆心角的度数是108 ，并补全条形统计图：‎ ‎ (2)预计2016年国庆节将有80万游客选择西宁周边游，请估计有多少万人会选择去贵德 ‎ (3)甲乙两个旅行团在青海湖、塔尔寺、原子城三个景点中．同时选择去同一个景点的概率是多少？请用面树状图或列表法加以说明，并列举所有等可能的结果．‎ ‎ 解：(1)由条形圈和扇形图可知，游“青海湖”的人数是15万人，占30%‎ 共接待游客人数为：15÷30%= 50(万人)，‎ ‎ “青海湖”所对应的圆心角的度数是：％=50（万人）‎ ‎ 塔尔寺人数为：24%50=12(万人)，补全条形统计图如图：‎ ‎ (2) ×80= 9.6（万人）‎ 答：估计将有9.6万人会选择去贵德旅游：‎ ‎(3)设A，B，C分别表示青海湖、塔尔寺、原子城 ‎ 乙 ‎ 甲 A B C A AA BA CA B AC BB CB C AC BC CC 由此可见，共有9种可能出现的结果，这些结果出现的可能性相等，其中同时选择去同一个景点的结果有3种．‎ ‎ ∴同时选择去同一个景点的概率是 ‎9．（2016荆州）为了弘扬荆州优秀传统文化，某中学举办了荆州文化知识大赛，其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答为0分且不扣分，赛后对全体参赛选手的答题情况进行了相关统计，整理并绘制成如下图表：‎ 组别 分数段 频数（人）‎ 频率 ‎1‎ ‎50≤x<60‎ ‎30‎ ‎0.1‎ ‎2‎ ‎60≤x<70‎ ‎45‎ ‎0.15‎ ‎3‎ ‎70≤x<80‎ ‎60‎ n ‎4‎ ‎80≤x<90‎ n ‎0.4‎ ‎5‎ ‎90≤x<100‎ ‎45‎ ‎0.15‎ 请根据图表信息，解答下列问题：‎ ‎(1)表中m=120，n=0.2；‎ ‎(2)补全频数分布直方图：‎ ‎(3)全体参赛选手成绩的中位数落在第几组；‎ ‎(4)若得分在80分以上（含80分）的选手可获奖，记者从所有参赛选手中随机采访1人，求这名选手恰好是获奖者的概率，‎ ‎ ‎ 解：(1)由表格可得，‎ 全体参赛的选手人数有：30÷0.1= 300，‎ 则m=300x0.4=120,n=60-300=0.2.‎ ‎(2)朴全的频数分布直方图如图所示，‎ 第9题答案图 ‎(3)∵35+45= 75,75+60 =135 ,135+120= 255,‎ ‎ ∴全体参赛选手成绩的中位数落在80≤x<90这一组，即第4组；‎ ‎ (4)由题意可得，，即这名选手恰好是获奖者的概率是0.55．‎ B组提高练习 ‎10．（2016重庆南开）有十张正面分别标有数字-3，-2，-1，0，l，2，3，4，5，6的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a．将该卡片上的数字加1记为b．则数字a,6使得关于戈的方程有解的概率为 ‎(提示：这个方程可以是一元一次方程，则a=0时方程有解，也可以是一元二次方程，则只需满足即可．）‎ ‎11．（2016重庆外语校）从-1，0，1，2，3五个数中，随机抽取一个数记为m，则使关于戈的不等式组有解，并且使函数与戈轴有交 ‎ 点的概率是．‎ ‎（提示：使关于z的不等式组有解，解不等式得：，则并且使函数与z轴有交点，当m=l时，是一次函数，当m≠1时，是二次函数，只需满足即可）‎ ‎12．某商场为了吸引顾客，设立了可以白由转动的转盘（如图，转盘被均匀分为20份），并规定：顾客每购买200元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得200元、100元、50元的购物券，‎ ‎ 凭购物券可以在该商场继续购物，如果顾客不愿意转 ‎ 转盘，那么可以直接获得购物券30元．‎ ‎ (1)求转动一次转盘获得购物券的概率；‎ ‎ (2)转转盘和直接获得购物券，你认为哪种方式对顾 客更合算？‎ 解：(1)转盘被均匀分为20份，转动一次转盘获得购物券的有10种情况，‎ ‎∴P（转动一次转盘获得购物券）‎ ‎(2) P（红色）=，P（黄色）=，P（绿色）= ‎ ‎（元 ‎∵40元>30元，‎ ‎∴选择转转盘对顾客更合算.‎