反比例函数的图象与性质教案(1)

反比例函数的图象与性质教案(1)

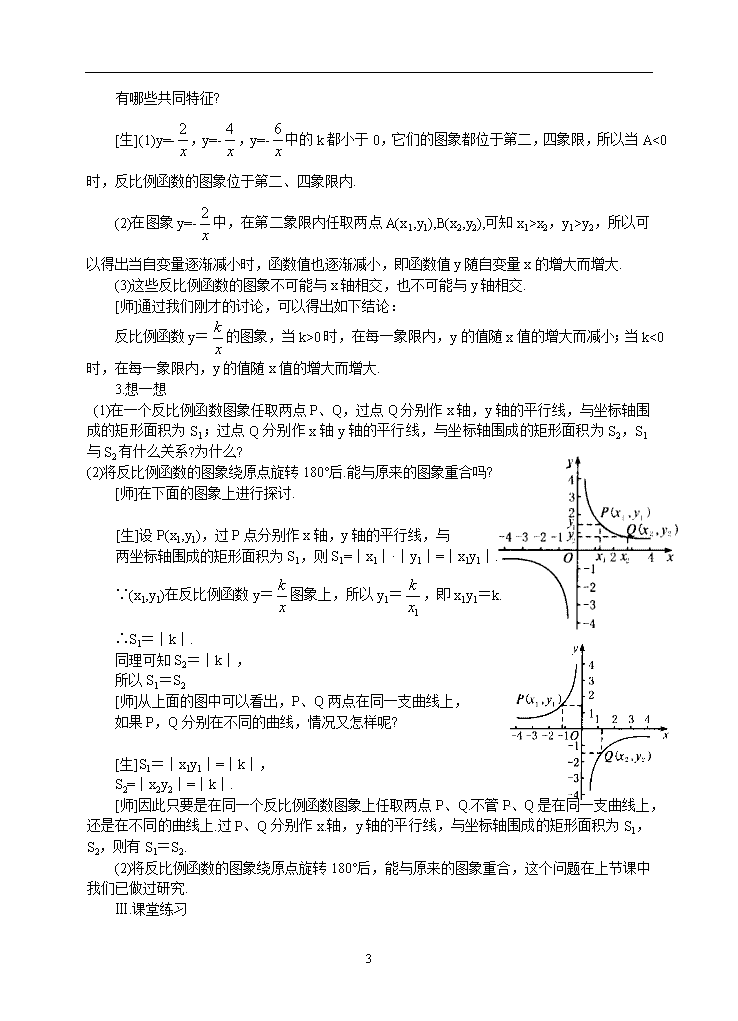
‎6.2.2 反比例函数的图象与性质(二)‎ 教学目标：‎ ‎ (一)教学知识点 ‎ 1.进一步巩固作反比例函数的图象.‎ ‎ 2.逐步提高从函数图象中获取信息的能力，探索并掌握反比例函数的主要性质.‎ ‎ (二)能力训练要求 ‎ 1.通过画反比例函数图象，训练学生的作图能力.‎ ‎ 2.通过从图象中获取信息.训练学生的识图能力.‎ ‎ 3.通过对图象性质的研究，训练学生的探索能力和语言组织能力.‎ ‎ (三)情感与价值观要求 ‎ 让学生积极投身于数学学习活动中，有助于培养他们的好奇心与求知欲.经过自己的努力得出的结论，不仅使他们记忆犹新，还能建立自信心.由学生自己思考再经过合作交流完成的数学活动，不仅能使学生学到知识，还能使他们互相增进友谊.‎ 教学重点：通过观察图象，概括反比例函数图象的共同特征，探索反比例函数的主要性质.‎ 教学难点：从反比例函数的图象中归纳总结反比例函数的主要性质.‎ 教学方法：教师引导学生类推归纳概括学习法.‎ 教具准备：多媒体课件 教学过程：‎ ‎ Ⅰ.创设问题情境，引入新课 ‎ [师]上节课我们学习了画反比例函数的图象，并通过图象总结出当k＞0时,函数图象的两个分支分别位于第一、三象限内；当k＜0时，函数图象的两个分支分别位于第二、四象限内.并讨论了反比例函数y=与y=-的图象的异同点.这是从函数的图象位于哪些象限来研究了反比例函数的.‎ ‎ 我们知道在学习正比例函数和一次函数图象时，还研究了当k＞0时，y的值随x的增大而增大，当k＜0时，y的值随x值的增大而减小，即函数值随自变量的变化而变化的情况，以及函数图象与x轴，y轴的交点坐标.本节课我们来研究一下反比例函数的有关性质.‎ ‎ Ⅱ. 新课讲解 ‎ 1.做—做 ‎ [师]观察反比例函数y=，y=,y=的形式，它们有什么共同点?‎ ‎ [生]表达式中的k都是大于零的.‎ ‎[师]大家的观察能力非同一般呐! ‎ 下面再用你们的慧眼观察它们的 图象，总结它们的共同特征.‎ 5‎ ‎(1)函数图象分别位于哪几个象限?‎ ‎(2)在每一个象限内，随着x值的增大.y的值是怎样变化 的?能说明这是为什么吗？‎ ‎(3)反比例函数的图象可能与x轴相交吗?可能与y轴相 交吗？为什么？‎ ‎ [师]请大家先独立思考，再互相交流得出结论.‎ ‎ [生](1)函数图象分别位于第一、三象限内.‎ ‎(2)从图象的变化趋势来看，当自变量x逐渐增大时，‎ 函数值y逐渐减小.‎ ‎ (3)因为图象在逐渐接近x轴,y轴，所以当自变量取很小或很大的数时，图象能与x轴y轴相交.‎ ‎ [师]大家同意他的观点吗?‎ ‎ [生]不同意(3)小的观点.‎ ‎ [师]能解释一下你的观点吗？‎ ‎ [生]从关系式y＝中看,因为x≠0，所以图象与y轴不可能能有交点；因为不论x取任何实数，2是常数，y＝永远也不为0，所以图象与x轴心也不可能有交点.‎ ‎ [师]对于(1)和(3)我不需要再说什么了，因为大家都回答的非常棒，不面我再补充—下(2).观察函数y＝的图象，在第一象限我任取两点A（x1,y1），B(x2,y2)，分别向x轴,y轴作垂线，找到对应的x1,x2,y1,y2,因为在坐标轴上能比较出x1与x2,y1与y2的大小，所以就可判断函数值的变化随自变址的变化是如何变化的.山图可知x1＜x2,y2＜y1,所以在第一象限内有y随x的增大而减小.‎ ‎ 同理可知在其他象限内y随x的增大而如何变化.大家可以分组验证上图中的其他五种情况.‎ ‎ [生]情况都一样.‎ ‎ [师]能不能总结一下.‎ ‎[生]当k>0时，函数图象分别位于第一、三象限 内，并且在每一个象限内，y随x的增大而减小.‎ ‎ 2.议一议 ‎[师]刚才我们研究了y＝，y＝,y=的图象的性质，‎ 下面用类推的方法来研究y＝-，y＝-,y=-的图象 5‎ 有哪些共同特征?‎ ‎ [生](1)y=-，y=-，y=-中的k都小于0，它们的图象都位于第二，四象限，所以当A<0时，反比例函数的图象位于第二、四象限内.‎ ‎ (2)在图象y=-中，在第二象限内任取两点A(x1,y1),B(x2,y2),可知x1>x2，y1>y2，所以可以得出当自变量逐渐减小时，函数值也逐渐减小，即函数值y随自变量x的增大而增大.‎ ‎ (3)这些反比例函数的图象不可能与x轴相交，也不可能与y轴相交.‎ ‎ [师]通过我们刚才的讨论，可以得出如下结论：‎ ‎ 反比例函数y＝的图象，当k>0时，在每一象限内，y的值随x值的增大而减小；当k<0时，在每一象限内，y的值随x值的增大而增大.‎ ‎ 3.想一想 ‎ (1)在一个反比例函数图象任取两点P、Q，过点Q分别作x轴，y轴的平行线，与坐标轴围成的矩形面积为S1；过点Q分别作x轴y轴的平行线，与坐标轴围成的矩形面积为S2，S1与S2有什么关系?为什么?‎ ‎(2)将反比例函数的图象绕原点旋转180°后.能与原来的图象重合吗?‎ ‎[师]在下面的图象上进行探讨.‎ ‎[生]设P(x1,y1)，过P点分别作x轴，y轴的平行线，与 两坐标轴围成的矩形面积为S1，则S1=｜x1｜·｜y1｜=｜x1y1｜.‎ ‎∵(x1,y1)在反比例函数y＝图象上，所以y1＝，即x1y1＝k.‎ ‎∴S1＝｜k｜.‎ ‎ 同理可知S2＝｜k｜，‎ ‎ 所以S1＝S2‎ ‎[师]从上面的图中可以看出，P、Q两点在同一支曲线上，‎ 如果P，Q分别在不同的曲线，情况又怎样呢?‎ ‎ [生]S1＝｜x1y1｜=｜k｜，‎ ‎ S2=｜x2y2｜=｜k｜.‎ ‎ [师]因此只要是在同一个反比例函数图象上任取两点P、Q.不管P、Q是在同一支曲线上，还是在不同的曲线上.过P、Q分别作x.轴，y轴的平行线，与坐标轴围成的矩形面积为S1，S2，则有S1＝S2.‎ ‎ (2)将反比例函数的图象绕原点旋转180°后，能与原来的图象重合，这个问题在上节课中我们已做过研究.‎ ‎ Ⅲ.课堂练习 5‎ ‎ P137‎ ‎ Ⅳ.课时小结 ‎ 本节课学习了如下内容.‎ ‎ 1.反比例函数y＝的图象，当k0时，在第一、三象限内，在每一象限内，y的值随，值的增大而减小；当k

查看更多