2012年随州中考数学试卷
随州市2012年初中毕业生学业考试
数学试题卷
一.选择题(本题有10个小题,每小题4分,共40分。每个小题给出的四个选项中,只有一个是正确的)
1.-2012的相反数是 ( )
A. B. C.-2012 D.2012
2.湿地旅游爱好者小明了解到鄂东南某市水资源总量为42.43亿立方米,其中42.43亿用科学记数法可表示为( )
A. 42.43×109 B. 4.243×108 C. 4.243×109 D. 0.4243×108
3.分式方程的解是( )
A.v=-20 B.V=5 C.V=-5 D.V=20
4.某校为了丰富校园文化,举行初中生书法大赛,决赛设置了6个获奖名额,共有ll名选手进入决赛,选手决赛得分均不相同.若知道某位选手的决赛得分,要判断他能否获奖,只需知道这11名选手决赛得分的( )
A.中位数 B.平均数 C.众数 D.方差
5.下列四个几何体中,主视图与左视图相同的几何体有( )
A.1个 B.2个 C.3个 D.4个
6.下列图形:①等腰梯形,②菱形,③函数的图象,④函数y=kx+b(k≠0)的图象,其中既是轴对称图形又是中心对称图形的有( )
A.①② B.①③ C.①②③ D.②③④
7.如图,AB是⊙O的直径,若∠BAC=350,则么∠ADC=( )
A.350 B.550 C.700 D.1100
8.若不等式组的解集为2
l)则△OAB的面积(用m表示)为( )
A. B. C. D.
二.填空题(本题有6个小题,每小题4分,共24分)
11.分解因式.4x2—9= .
12.函数中自变量x的取值范围是 .
13.等腰三角形的周长为16,其一边长为6,则另两边为 .
14.如图,点D、E分别在AB、AC上,且∠ABC=∠AED.若DE=4,AE=5,BC=8;则AB的长为 .
15.平面内不同的两点确定一条直线,不同的三点最多确定三条直线,若平面内的不同的n个点最多可确定15条直线,则n的值为 .
16.设a2+2a-1=0,b4-2b2-1=0,且1-ab2≠0,则= .
三.解答题(本题有9个小题,共86分)
17.(本小题满分8分)计算:(一1)3++2sin 600-
18.(本小题满分8分)先化简,再求值:。其中.
19. (本小题满分8分)如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:(1)ΔABD≌ΔACD;(2)BE=CE
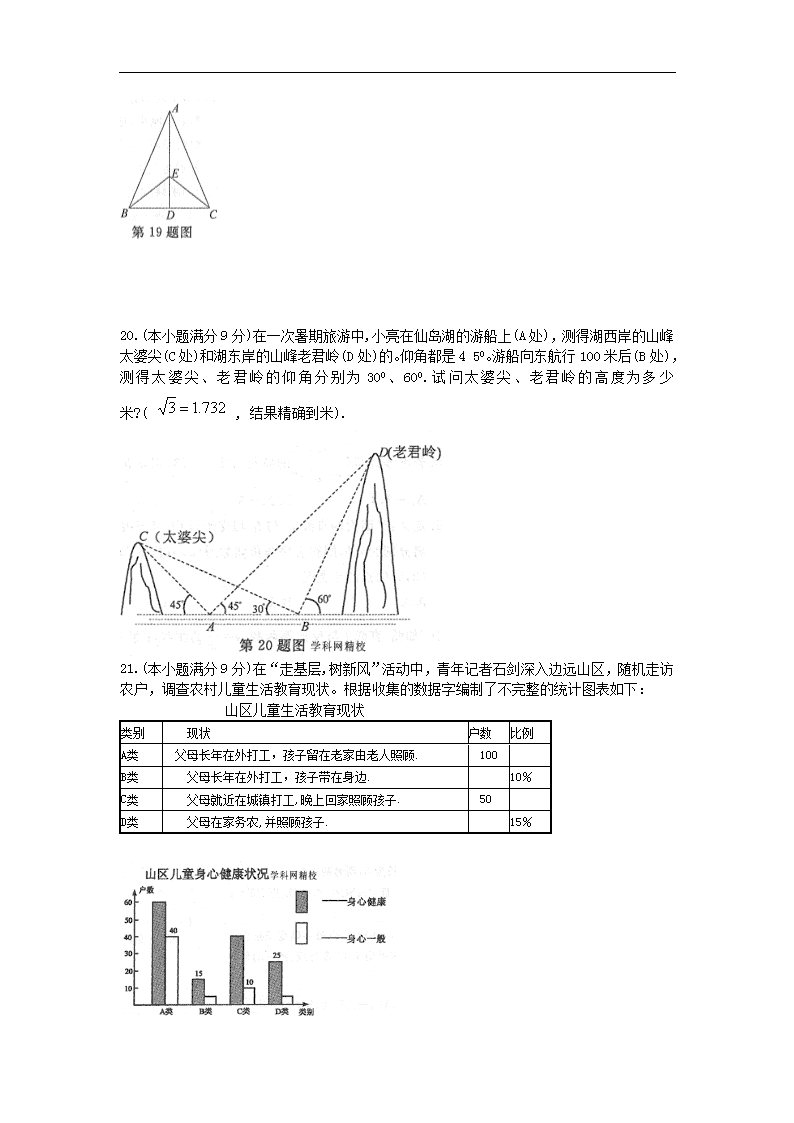
20.(本小题满分9分)在一次暑期旅游中,小亮在仙岛湖的游船上(A处),测得湖西岸的山峰太婆尖(C处)和湖东岸的山峰老君岭(D处)的。仰角都是4 50。游船向东航行100米后(B处),测得太婆尖、老君岭的仰角分别为300、600.试问太婆尖、老君岭的高度为多少米?( , 结果精确到米).
21.(本小题满分9分)在“走基层,树新风”活动中,青年记者石剑深入边远山区,随机走访农户,调查农村儿童生活教育现状。根据收集的数据字编制了不完整的统计图表如下:
山区儿童生活教育现状
类别
现状
户数
比例
A类
父母长年在外打工,孩子留在老家由老人照顾.
100
B类
父母长年在外打工,孩子带在身边.
10%
C类
父母就近在城镇打工,晚上回家照顾孩子.
50
D类
父母在家务农,并照顾孩子.
15%
请你用学过的统计知识,解决问题:
(1)记者石剑走访了边远山区多少家农户?
(2)将统计图表中的空缺数据正确填写完整;
(3)分析数据后,请你提一条合理建议.
22.(本小题满分9分)如图所示,一个大正方形地面上,编号为l ,2 ,3,4的地块,是四个全等的等腰直角三角形空地,中间是小正方形绿色草坪。一名训练有素的跳伞运动员,每次跳伞都能落在大正方形地面上.
(1)求跳伞运动员一次跳伞落在草坪上的概率;
(2)求跳伞运动员两次跳伞都落在草坪上的概率.
23.(本小题满分10分)如图,已知直角梯形ABCD ,∠B=900。,AD∥BC,并且AD+BC=CD,0为AB的中点.
(1)求证:以AB为直径的⊙D与斜腰CD相切;
(2)若OC=8 cm,OD=6 cm,求CD的长.
24.(本小题满分12分)一列快车由甲地开往乙地,一列慢车由乙地开往甲地, 两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示;慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段0C所示。根据图象进行以下研究。
解读信息:
(1)甲、乙两地之间的距离为 km;
(2)线段AB的解析式为 ;
线段OC的解析式为 ;
问题解决:
(3)设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数
的图象。
25.(本小题满分13分)在-次数学活动课上,老师出了-道题:
(1)解方程x2-2x-3=0.
巡视后老师发现同学们解此题的方法有公式法、配方法和十字相乘法(分解因式法)。
接着,老师请大家用自己熟悉的方法解第二道题:
(2)解关于x的方程mx2+(m一3)x一3=0(m为常数,且m≠0).
老师继续巡视,及时观察、点拨大家.再接着,老师将第二道题变式为第三道题:
(3)已知关于x的函数y=mx2+(m-3)x-3(m为常数).
①求证:不论m为何值,此函数的图象恒过x轴、y轴上的两个定点(设x轴上的定点为A,y轴上的定点为C);
②若m≠0时,设此函数的图象与x轴的另一个交点为反B,当△ABC为锐角三角形时,求m的取值范围;当△ABC为钝角三角形时,观察图象,直接写出m的取值范围.
请你也用自己熟悉的方法解上述三道题.
随州市2012年初中毕业生升学考试
数学试题答案及评分标准
一.选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
B
A
D
D
B
A
C
B
二.填空题:
11.(2x+3) (2x-3) 12.
13.6和4或5和5 14.10
15.6 16.-32
三解答题:
17. 解:=……………………6分
=-1 ……………………2分
18.解:
…………………6分
当时,则原式= ……………………2分
19.证明:(1)在⊿ABD和⊿ACD中
∵D是BC的中点,
∵⊿ABC≌⊿ACD. (SSS) ……………………4分
(2)由(1)知⊿ABD≌⊿ACD
∠BAD=∠CAD
即:∠BAE=∠CAE
在⊿ABE和⊿ACE中,
⊿ABE≌⊿ACE (SAS)
BE=CE
(其他正确证法同样给分) ………………4分
20.解:设太婆尖高h1米,老君岭高h2米,依题意,有
………4分(米)………2分
(米)…………2分
答:太婆尖高度为137米,老君岭高度为237米。 …………1分
21. 解:(1)由扇形图和表格可知,C类占25%,A类占:100%-15%-25%-10%=50%
A、B、C、D类各占50%,10%,25%,15%
A、B、C、D类各户数100,20,50,30,总户数为200.记者石剑走访了200户农家。 …………2分
(2)补全图表空缺数据.
类别
现状
户数
比例
A类
父母常年在外打工孩子留在老家由老人照顾
100
50%
B类
父母常年在外打工,孩子带在身边
20
10%
C类
父母就近在城镇打工,晚上回家照顾孩子
50
25%
D类
父母在家务农,并照顾孩子
30
15%
——身心健康
——身心一般
山区儿童各类所占比例
…………2分
………2分 …………2分
(3)由图表可知孩子带在身边有益孩子的身心健康,建议社会关心留守儿童的生活状况.
…………1分
22.解:(1)一次跳伞落在草坪上的概率P(一次跳伞落在草坪上)=(将大正方形分成8块等腰直角三角形) …………5分
(2)每次跳伞落在8个等腰直角三角形的可能性是相等的,
用树状图
………
共有8×8=64个不同结果
其中两次落在草坪上有:
共有4×4=16个不同结果.
所以两次跳伞都落在草坪上的概率为P(两次跳伞都落在草坪上)= . …………4分
23.证明:(方法一)
过AB的中点O作OE⊥CD于E.
S梯形ABCD=(AD+BC) •AB=(AD+BC) •OA
=2(AD•OA+BC•OB)
=2(S⊿OAD +S⊿OBC)
由S梯形ABCD =S⊿OBC+ S⊿OAD+ S⊿OCD
∴S⊿OBC+ S⊿OAD=S⊿OCD
∴AD•OA+BC•OA=CD·OE
∴(AD+BC) ·OA=CD·OE又AD+BC=CD
∴OA=OE,∴E点在以AB为直径的⊙O上,又OE⊥CD
∴CD是⊙O的切线
即:CD与⊙O相切 …………5分
方法二:
在CD上取中点F,连接OF,有梯形中位线可知OF=(AD+BC)= CD
∴O点在以CD为直径的⊙F上
∴∠1=∠3,∠2=∠4,又OF∥AD∥BC
∴∠5=∠3,∠6=∠4
∴∠1=∠5, ∠2=∠6
在CD上取点E,且DE=DA,则CE=CB
∴⊿OAD≌⊿OED, ⊿OBC≌⊿OEC
∴∠A=∠OED=90°, ∠B=∠OEC=90°
∴OE⊥CD,且OE的长为⊙O的半径,∴以AB为直径的⊙O与CD相切于E。由CD为直径的⊙F与AB相切于O,则OD⊥OC.
∴CD= …………5分
24. (1)甲、乙两地之间的距离为 450 km; …………2分
(2)问题解决:线段AB的解析式为 y1=450-150 x (0≤x≤3); …………3分
线段OC的解析式为 y2=75x (0≤x≤6) ; …………3分
(3)y= …………2分
其图象为折线图AE-EF-FC
…………2分
25.解:(1)由x2-2x-3=0,得(x+1)(x-3)=0∴x1=1,x2=3 …………3分
(2)方法一:由mx2+(m-3)x-3=0得(x+1)·(mx-3)=0
∵m≠0, ∴x1=-1,x2= …………3分
方法2:由公式法:
∴x1=-1,x2=
(3)①1°当m=0时,函数y= mx2+(m-3)x-3为y=-3x-3,令y=0,得x=-1
令x=0,则y=-3. ∴直线y=-3x-3过定点A(-1,0),C(0,-3) …………2分
2°当m≠0时,函数y= mx2+(m-3)x-3为y=(x+1)·(mx-3)
∴抛物线y=(x+1)·(mx-3)恒过两定点A(-1,0),C(0,-3)和B(,0)
②当m>0时,由①可知抛物线开口向上,且过点A(-1,0),C(0,-3)和
B(,0), …………1分
观察图象,可知,当⊿ABC为Rt⊿时,
则⊿AOC∽⊿COB∴
∴∴32=1×
∴OB=9.即B(9,0)
∴当.即:m>
当m>时,⊿ABC为锐角三角形 …………2分
②观察图象可知
当090º,
当m<0且m≠-3时,点B在x轴的负半轴上,B与A不重合.
∴⊿ABC中的∠ABC>90º
∴⊿ABC是钝角三角形.
∴当0
查看更多