- 2021-04-23 发布 |
- 37.5 KB |
- 26页

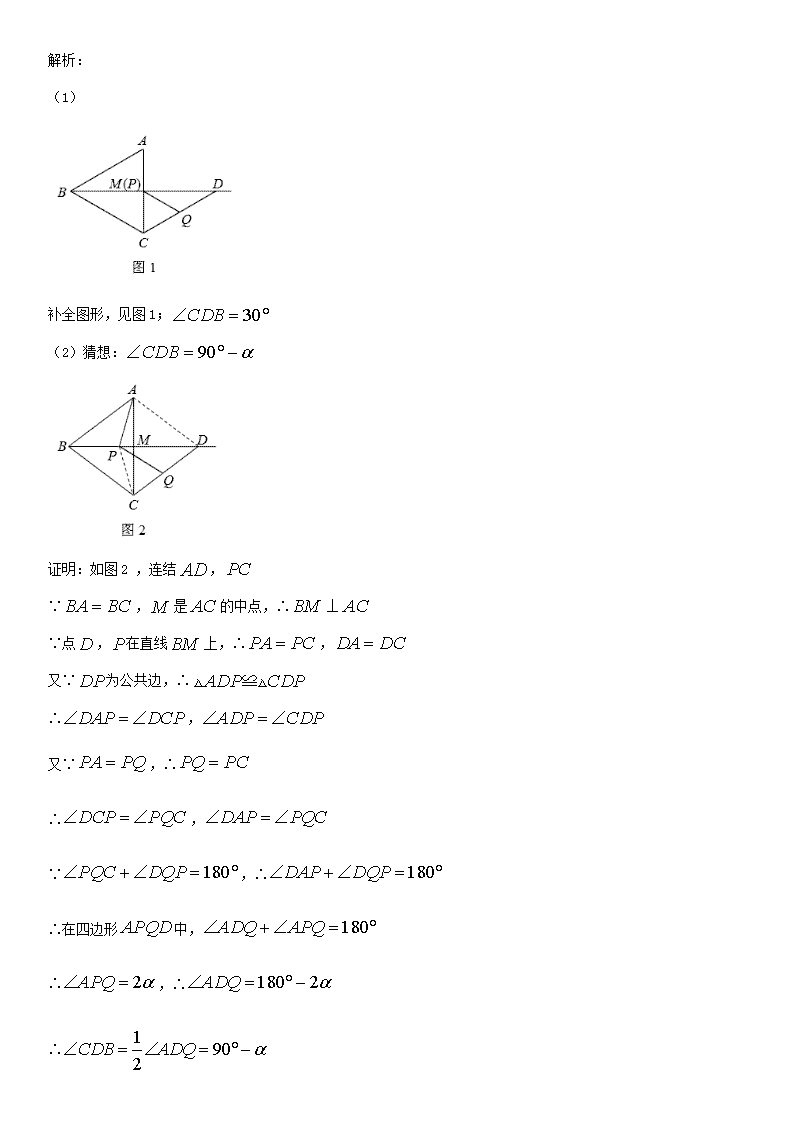
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版中考数学二轮复习专题练习下几何问题-线段的旋转
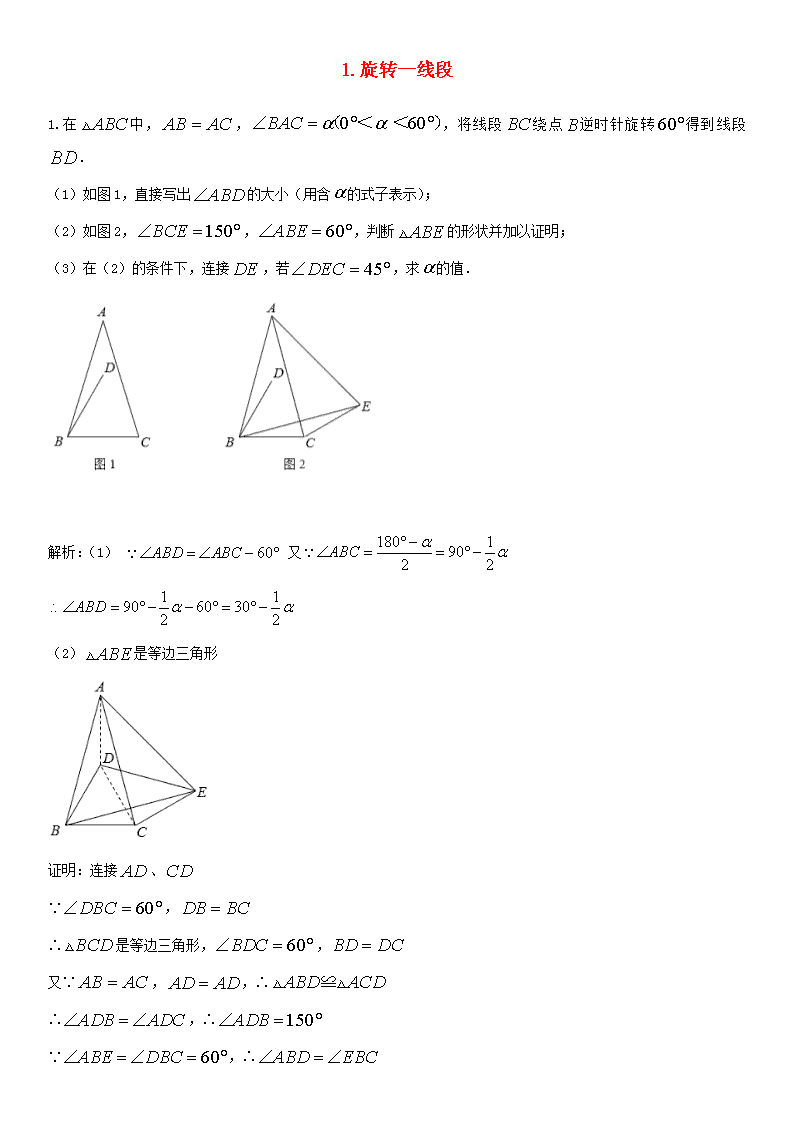
1.旋转—线段 1.在中,,,将线段绕点逆时针旋转得到线段. (1)如图1,直接写出的大小(用含的式子表示); (2)如图2,,,判断的形状并加以证明; (3)在(2)的条件下,连接,若,求的值. 解析:(1) 又 (2)是等边三角形 证明:连接、 ∵, ∴是等边三角形,, 又∵,,∴ ∴,∴ ∵,∴ 又∵, ∴,∴ ∴是等边三角形 (3)解:∵是等边三角形,∴ ∴ 又∵,∴, ∴, ∵ , ∴. 2.在中,,,是的中点,是线段上的动点,将线段绕点顺时针旋转得到线段. (1)若且点与点重合(如图1),线段的延长线交射线于点,请补全图形,并写出的度数; (2)在图2中,点不与点,重合,线段的延长线与射线交于点,猜想的大小(用含的代数式表示),并加以证明; (3)对于适当大小的,当点在线段上运动到某一位置(不与点,重合)时,能使得线段的延长线与射线交于点,且,请直接写出的范围. 解析: (1) 补全图形,见图1; (2)猜想: 证明:如图2 ,连结, ∵,是的中点,∴ ∵点,在直线上,∴, 又∵为公共边,∴ ∴, 又∵,∴ ∴, ∵,∴ ∴在四边形中, ∴,∴ ∴ (3) 提示:由(2)知,且 ∴ ∵点不与点,重合,∴ ∴,∴ 3.如图1,边长为4的正方形中,点在边上(不与点,重合),点在边上(不与点,重合). 第一次操作:将线段绕点顺时针旋转,当点落在正方形上时,记为点; 第二次操作:将线段绕点顺时针旋转,当点落在正方形上时,记为点; 依此操作下去… (1)图2中的是经过两次操作后得到的,其形状为____________,求此时线段的长; (2)若经过三次操作可得到四边形. ①请判断四边形的形状为____________,此时与的数量关系是_________; ②以①中的结论为前提,设的长为,四边形的面积为,求与的函数关系式及的取值范围. (3)若经过多次操作可得到首尾顺次相接的多边形,其最大边数是多少?它可能是正多边形吗?如果是,请直接写出其边长;如果不是,请说明理由. 解析: (1)由旋转可得: 为等边三角形 ∵四边形是正方形,∴, ∵,∴ ∴, ∴三角形是等腰直角三角形 设的长为,则, 在中, ∴ 解得,(舍去) ∴ (2)①四边形 的形状为正方形,此时 .理由如下: 依题意画出图形,如答图1所示: 由旋转性质可知, , 四边形 的形状为正方形. , . , . 在 与 中, . ②利用①中结论,易证均为全等三角形, , . 在中, ∴ ∵ ∴当时,取得最小值;当时, ∴的取值范围是 (3)经过多次操作可得到首尾顺次相接的多边形,其最大边数是,它可能为正多边形,边长为. 如答图2所示,粗线部分是由线段 经过次操作所形成的正八边形. 设边长 ,则 , ,解得:. 4.已知,四边形是正方形,点在直线上,点在直线上(、不与正方形顶点重合,且在的同侧),,于点,交直线于点,将线段绕点逆时针旋转得到线段,连结. (1)如图1,当点与点分别在线段与线段上时. ①求证:; ②求证:四边形是菱形; (2)如图2,当点与点分别在线段与线段的延长线上时,猜想四边形是怎样的特殊四边形,并证明你的猜想. 解析: (1) ①作于点 ∵,∴ 又∵,∴ ②∵于,∴ 又∵ ∴ ∵四边形是正方形,于点 ∴, ∴,∴ ∵,∴ ∵,,∴ ∴四边形是平行四边形 又∵,∴是菱形 (2)四边形是菱形 证明:∵四边形是正方形,于 ∴ ∴ ∴, ∵,∴ ∴ ∴ 又∵, ∴,∴ ∵,∴ 又∵,,∴ ∴四边形是平行四边形 又∵,∴平行四边形是菱形 5.如图1,在正方形中,点、分别在边、上,且平分. (1)求证:;(本小问不予评分,自行查看解析) (2)当平分时(如图2),将线段绕点逆时针旋转,旋转后的线段分别交、于点、,若正方形的边长为4,求的面积. 解析: (1)证明: 将绕点顺时针旋转到 则,, ∵,∴ ∴ ∵,∴ ∴ ∴,∴ ∵,∴ (2) 过作于 则, ∴,∴ ∵,∴ ∵平分,平分 ∴ ∴,∴ ∴,∴, ∴, 过作于,设 又 ∴,∴ ,∴ , ∴,∴ 过作交于,则是梯形的中位线 设, , ∴ , ,∴ 过作于,则 ∴ 6.在中,,,点是的中点,,垂足为点,连接. (1)如图1,与的数量关系是___________; (2)如图2,若是线段上一动点(点不与点、重合),连接,将线段绕点逆时针旋转,得到线段,连接,请猜想、、三者之间的数量关系,并证明你的结论; (3)若点是线段延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出、、三者之间的数量关系_____________. 解析:(1) , , 点 是 的中点, , 为等边三角形, , ; 故答案为(或) (2) (或) 证明:∵在中,, ∴ ∵是的中点,∴ ∴是等边三角形,∴ ∴ 即 又∵,∴ ∴ ∵,∴,∵ ∴ (3)如图, 与(2)一样可证明 , , 而 , , (或) 7.在中,,,是的中点,为射线上任意一点,将线段绕点逆时针旋转得到线段,连接,过点作,交直线于点. (1)如图1,当点在线段上时,判断与的数量关系并加以证明; (2)如图2,当点在线段的延长线上时,其它条件不变,你在(1)中得到的结论是否成立,请说明理由; (3)当点从的中点移动到点时,直接写出线段的中点所经过的路径长. 解析:(1) 证明: 连接,延长交于 ∵,∴ ∵是的中点,∴为的中点, ∴是的中位线,∴ ∵,∴ ∵,∴ ∵, ∴, ∴ ∵和都是等腰直角三角形 ∴,∴ ∴,∴ (2)成立 证明:连接,设交于 同理可证, , ∵,∴ ∴,∴ ∴ (3)线段的中点所经过的路径长为 提示:延长交于,取中点,连接、、 则, ∴,∴ ∴ ∵, ∴, ∴ ,∴ ∴ ∴,是定值 ∴线段的中点所经过的路径是一条线段 当点与点重合时,是的中点 连接、,则是的中位线 由(1)知, ∴ 当点与点重合时,点与点重合,此时为的中点 ∴点所经过的路径长即为图中的长 ∵,∴,, ∴ 8.已知,,是过点的直线,于点. (1)如图1,求:; (2)当绕点旋转到如图(2)和图(3)两个位置时,猜想、、满足的关系式,并给予证明; (3)在在绕点旋转过程中,当, 时,则_________,_________. 解析: (1) 证明:如图1,过点作,交于点 ∵, ∴ ∵四边形内角和为 ∴ ∵,∴ 又,∴ ∴, ∴为等腰直角三角形 ∴ 又,∴ ∴ (2)图2中,;图3中, 证明:如图2,过点作,交于点 ∵, ∴ ∵,∴ 又,∴ ∴, ∴为等腰直角三角形 ∴ 又,∴ ∴ 如图3,过点作,交于点 ∵, ∴ ∵,∴ 又,∴ ∴, ∴为等腰直角三角形 ∴ 又,∴ ∴ (3),或 提示:过点作,交于点,连接, 和都是等腰直角三角形 ∴ ∵,∴ 当、两点在直线异侧时 则,∴ ∵,∴,, ∴ ∵;∴ ∴ 当、两点在直线同侧时 ,∴ ∵,∴,, ∴ ∵;∴ ∴ 9.在中,过点作交于点,将线段绕点逆时针旋转得到线段(如图1). (1)在图1中画图探究: ①当为射线上任意一点(不与点重合)时,连结,将线段绕点逆时针旋转得到线段,判断直线与直线的位置关系并加以证明; ②当为线段的延长线上任意一点时,连结,将线段绕点逆时针旋转得到线段,判断直线与直线的位置关系,画出图形并直接写出你的结论. (2)若,,,在①的条件下,设,,求与之间的函数关系式,并写出自变量的取值范围. 解析:(1)①直线与直线的位置关系为互相垂直. 证明:如图,设直线与直线的交点为. ∵线段、分别绕点逆时针旋转依次得到线段、. ∴,,. ∵,. ∴,∴. ∴,∴,∴. ∴. ② 按题目要求所画图形见图1,直线与直线的位置关系为互相垂直. (2)∵四边形是平行四边形,∴. ∵,,. ∴,. 可得 由(1)可得四边形为正方形 ∴ ① 如图2,当点在线段的延长线上时 (已证) 四边形为平行四边形 又 四边形中且 四边形为正方形 . ∴ 即 ② 如图3,当点在线段上(不与、两点重合)时 ∵,. ∴ 即 ③当点与点重合时,即时,不存在. 综上所述,与之间的函数关系式及自变量的取值范围是 或. 10.在中,,为中点,为边的高,点在边上,点在线段上,且. (1)如图l,当时,线段与的数量关系为___________; (2)如图2,当时,求证:; (3)如图3,在(2)的条件下,将射线绕点顺时针旋转,交边于点,连接、,若,,求线段的长. 解析: (1) 提示:连接, ∵ , ,∴ , , ∵ 为 边上的中点,∴ ,且 , ∴ ∵ ,∴ ,且 , ∴ , 在 与 中, ∴ (2) 连接 ∵ , 为 中点, ∴ , , ∵ 为 边的高,∴ ∵ ,∴ ∴ ∴ ,∴ ∵ ∴ (3)由,可设,则 由(2)知,∴ ∴ , , ,, 在 中, ∴,解得 (舍去负值) ∴ , , , , , 连接 ,,由(2)知 ∴,∴ ∴ ∵ ,∴ , ∴ ,∴ ,∴ ∵ ,∴ ∴ ,∴ ∴ ,∴查看更多