北京中考复习专题练习26题综合练习

北京中考复习专题练习26题综合练习

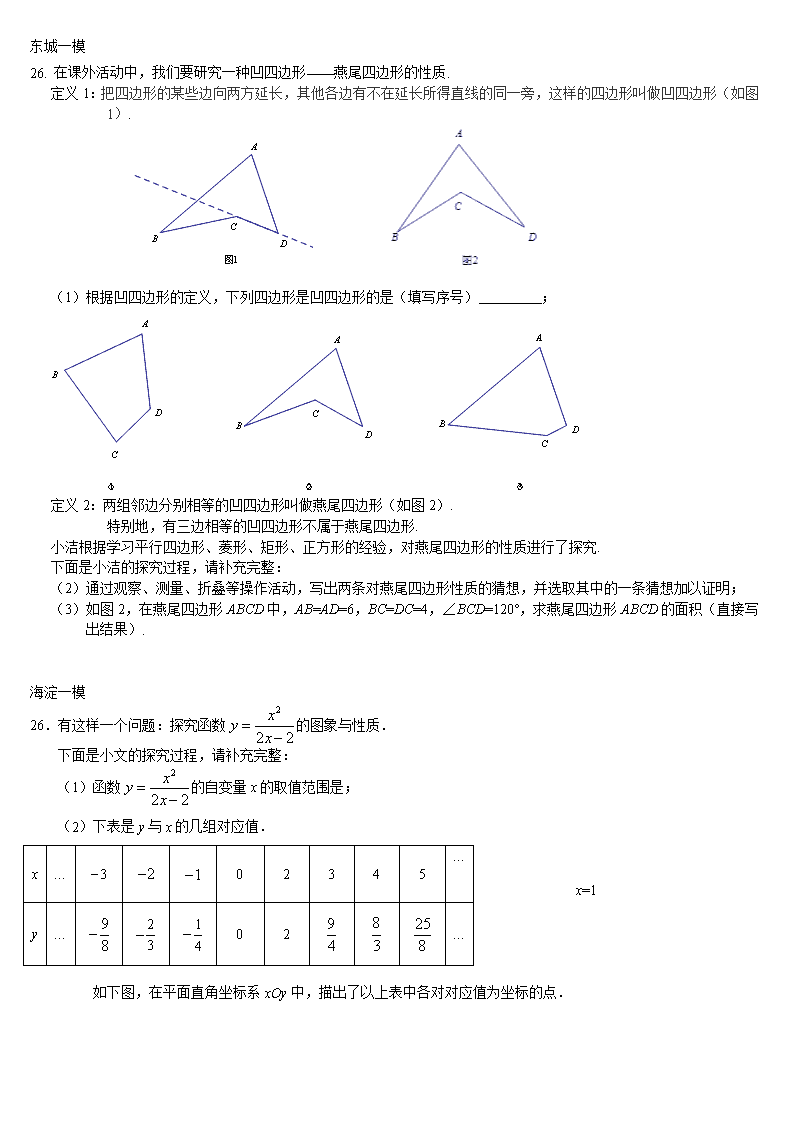
东城一模 ‎26. 在课外活动中，我们要研究一种凹四边形——燕尾四边形的性质. ‎ 定义1：把四边形的某些边向两方延长，其他各边有不在延长所得直线的同一旁，这样的四边形叫做凹四边形（如图1）.‎ ‎ ‎ ‎（1）根据凹四边形的定义，下列四边形是凹四边形的是（填写序号） ；‎ 定义2：两组邻边分别相等的凹四边形叫做燕尾四边形（如图2）.‎ 特别地，有三边相等的凹四边形不属于燕尾四边形.‎ 小洁根据学习平行四边形、菱形、矩形、正方形的经验，对燕尾四边形的性质进行了探究.‎ 下面是小洁的探究过程，请补充完整：‎ ‎（2）通过观察、测量、折叠等操作活动，写出两条对燕尾四边形性质的猜想，并选取其中的一条猜想加以证明；‎ ‎（3）如图2，在燕尾四边形ABCD中，AB=AD=6，BC=DC=4，∠BCD=120°，求燕尾四边形ABCD的面积（直接写出结果）.‎ 海淀一模 ‎26．有这样一个问题：探究函数的图象与性质．‎ 下面是小文的探究过程，请补充完整：‎ ‎（1）函数的自变量x的取值范围是； ‎ ‎（2）下表是y与x的几组对应值．‎ x ‎…‎ ‎0‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ x=1‎ ‎…‎ y ‎…‎ ‎0‎ ‎2‎ ‎…‎ 如下图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．‎ ‎①观察图中各点的位置发现：点和，和，和，和均关于某点中心对称，则该点的坐标为； ‎ ‎②小文分析函数的表达式发现：当时,该函数的最大值为0，则该函数图象在直线左侧的最高点的坐标为；‎ ‎（3）小文补充了该函数图象上两个点（），（），‎ ‎①在上图中描出这两个点，并画出该函数的图象；‎ ‎②写出该函数的一条性质：________________．‎ 大兴一模 ‎26.有这样一个问题：探究方程的实数根的个数.‎ 小芳想起了曾经解决的一个问题：通过函数图象探究方程的实数根的个数，她想到了如下的几个方法：‎ 方法1：方程的根可以看作是抛物线与直线（即x轴）交点的横坐标;这两个图象的交点个数即是方程的实数根的个数.‎ 方法2：将方程变形成 ，那么方程的根也可以看作是抛物线与直线+1交点的横坐标；这两个图象的交点个数即是方程的实数根的个数.‎ 方法3：由于x≠0,将方程变形成+3 =，那么方程的根也可以看作是直线+3与双曲线交点的横坐标；这两个图象的交点个数即是方程的实数根的个数.‎ 她类比上述方法，借助函数图象的交点个数对方程的实数根的个数进行了探究. ‎ ‎ 下面是小芳的探究过程，请补充完成：‎ ‎ (1) x=0 方程的根；(填”是”或”不是”)‎ ‎ (2) 方程的根可以看作 是函数 与函数 的图象交点的横坐标;‎ ‎ (3) 在同一坐标系中画出两个函数的图象;‎ ‎(4)观察图象可得, 方程的实数根的个数是 个.‎ 房山一模 ‎26.小东根据学习函数的经验，对函数的图象与性质进行了探究．下面是小东的探究过程，请补充完整，并解决相关问题：‎ ‎（1）函数的自变量x的取值范围是 ；‎ ‎（2）下表是y与x的几组对应值. ‎ x ‎…‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎…‎ ‎2‎ ‎4‎ ‎2‎ m ‎…‎ 表中m的值为________________；‎ ‎（3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点. 根据描出 的点，画出函数的大致图象；‎ ‎（4）结合函数图象，请写出函数 的一条性质：______________________________.‎ ‎（5）解决问题：如果函数与直线y=a的交点有2个，‎ 那么a的取值范围是______________ .‎ 顺义一模 ‎26．某“数学兴趣小组”根据学习函数的经验，对函数的图象和性质进行了探究，探究过程如下，请补充完整：‎ ‎（1）该函数的自变量x的取值范围是　　　　；‎ ‎（2）同学们先找到y与x的几组对应值，然后在下图的平面直角坐标系xOy中，描出各对对应值为坐标的点．请你根据描出的点，画出该函数的图象；‎ ‎（3）结合画出的函数图象，写出该函数的一条性质：．‎ 通州一模 ‎26．已知y是x的函数，自变量x的取值范围是x>0，下表是y与x的几组对应值.‎ x ‎…‎ ‎1‎ ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ ‎9‎ ‎…‎ y ‎…‎ ‎3.92‎ ‎1.95‎ ‎0.98‎ ‎0.78‎ ‎2.44‎ ‎2.44‎ ‎0.78‎ ‎…‎ 小风根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象和性质进行了探究.‎ 下面是小风的探究过程，请补充完整：‎ ‎（1）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象；‎ ‎（2）根据画出的函数图象，写出：‎ ‎①x=7对应的函数值y约为______________.‎ ‎②该函数的一条性质：______________________________________________________.‎ 西城一模 ‎26．（5分）阅读下列材料：‎ 某种型号的温控水箱的工作过程是：接通电源后，在初始温度20℃下加热水箱中的水；当水温达到设定温度80℃时，加热停止；此后水箱中的水温开始逐渐下降，当下降到20℃时，再次自动加热水箱中的水至80℃时，加热停止；当水箱中的水温下降到20℃时，再次自动加热，…，按照以上方式不断循环．‎ 小明根据学习函数的经验，对该型号温控水箱中的水温随时间变化的规律进行了探究．发现水温y是时间x的函数，其中y（单位：℃）表示水箱中水的温度．x（单位：min）表示接通电源后的时间．‎ 下面是小明的探究过程，请补充完整：‎ ‎（1）下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况 接通电源后的时间x ‎（单位：min）‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ ‎10‎ ‎16‎ ‎18‎ ‎20‎ ‎21‎ ‎24‎ ‎32‎ ‎…‎ 水箱中水的温度y ‎（单位：℃）‎ ‎20‎ ‎35‎ ‎50‎ ‎65‎ ‎80‎ ‎64‎ ‎40‎ ‎32‎ ‎20‎ m ‎80‎ ‎64‎ ‎40‎ ‎20‎ ‎…‎ m的值为　　；‎ ‎（2）①当0≤x≤4时，写出一个符合表中数据的函数解析式　　；‎ 当4＜x≤16时，写出一个符合表中数据 的函数解析式　　；‎ ‎②如图，在平面直角坐标系xOy中，描 出了上表中部分数据对应的点，根据描出的 点，画出当0≤x≤32时，温度y随时间x变化的函数图象：‎ ‎（3）如果水温y随时间x的变化规律不变，预测水温第8次达到40℃时，距离接通电源　　min．‎ 门头沟一模 ‎26.在一节数学实践课上，老师出示了这样一道题，‎ 如图26-1，在锐角三角形ABC中，∠A、∠B、∠C所对边分别是a、b、c,‎ 请用a、c、∠B表示.‎ ‎26-1‎ ‎26-2‎ 经过同学们的思考后，‎ 甲同学说：要将锐角三角形转化为直角三角形来解决，并且不能破坏∠B，因此可以经过点A，作AD⊥BC于点D,如图26-2，大家认同；‎ 乙同学说要想得到要在Rt△ABD或Rt△ACD中解决；‎ 丙同学说那就要先求出________,_______；(用含c，∠B的三角函数表示)‎ 丁同学顺着他们的思路，求出=AD2+DC2=_____________(其中)；‎ 请利用丁同学的结论解决如下问题：‎ 如图26-3，在四边形ABCD中，,,.‎ 求AC的长（补全图形，直接写出结果即可）.‎ 平谷一模 ‎26．有这样一个问题：探究函数的图象与性质． 小军根据学习函数的经验， 对函数的图象与性质进行了探究． 下面是小军的探究过程， 请补充完整：‎ ‎（1）函数的自变量x的取值范围是 ；‎ ‎（2）下表是y与x的几组对应值 x ‎﹣2‎ ‎﹣1.9‎ ‎﹣1.5‎ ‎﹣1‎ ‎﹣0.5‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎2‎ ‎1.60‎ ‎0.80‎ ‎0‎ ‎﹣0.72‎ ‎﹣1.41‎ ‎﹣0.37‎ ‎0‎ ‎0.76‎ ‎1.55‎ ‎…‎ 在平面直角坐标系xOy中， 描出了以上表中各对对应值为坐标的点，根据描出的点， 画出该函数的图象；‎ ‎（3）观察图象，函数的最小值是 ；‎ ‎（4）进一步探究，结合函数的图象， 写出该函数的一条性质（函数最小值除外）： ．‎ 燕山一模 ‎26．有这样一个问题：探究函数的图象和性质.‎ ‎ 小奥根据学习函数的经验，对函数的图象和性质进行了探究.‎ 下面是小奥的探究过程，请补充完整：‎ ‎（1）函数的自变量x的取值范围是 ；‎ ‎（2）下表是y与x的几组对应值：‎ x ‎…‎ ‎-5‎ ‎-4‎ ‎-2‎ ‎-1‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎…‎ y ‎…‎ ‎-2‎ ‎2‎ m ‎…‎ 求m的值；‎ ‎（3）如下图，在平面直角坐标系xoy中,描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象；‎ ‎ ‎ ‎(4)进一步探究发现，该函数图象在第一象限内的最低点的坐标是（2，2）.结合函数图象，写出该函数的其他性质（一条即可）： .‎ 丰台一模 ‎26．【问题情境】‎ ‎ 已知矩形的面积为a（a为常数，），当该矩形的长为多少时，它的周长 最小?最小值是多少?‎ ‎【数学模型】‎ 设该矩形的长为x，周长为y，则y与x的函数表达式为．‎ ‎【探索研究】‎ 小彬借鉴以前研究函数的经验，先探索函数的图象性质．‎ ‎（1）结合问题情境，函数的自变量x的取值范围是，‎ 下表是y与x的几组对应值．‎ x ‎…‎ ‎1‎ ‎2‎ ‎3‎ m ‎…‎ y ‎…‎ ‎2‎ ‎…‎ ‎①写出m的值；‎ ‎②画出该函数图象，结合图象，得出当x =______时，y有最小值，y最小=________；‎ ‎【解决问题】‎ ‎（2）直接写出“问题情境”中问题的结论．‎ 怀柔一模 ‎26．已知y是x的函数，下表是y与x的几组对应值. x ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎…‎ y ‎0‎ ‎1‎ ‎2‎ ‎…‎ 小聪根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的表达式，图象和性质进行了探究. 下面是小聪的探究过程，请补充完整:‎ ‎(1)根据上述表格所反映出的y与x之间的变化规律，‎ 写出该函数的表达式: ;‎ ‎ (2)该函数自变量x的取值范围是 ;‎ ‎(3)如图，在平面直角坐标系xOy中，描出上表中各对对应值为 坐标的点的位置（近似即可），根据描出的点，画出该函数的图象;‎ ‎(4)根据画出的函数图象，写出该函数的一条性质: .‎ 石景山一模 ‎26．（1）定义：把四边形的某些边向两方延长，其他各边有不在延长所得直线的同一旁，‎ ‎ 这样的四边形叫做凹四边形．如图1，四边形为凹四边形．‎ ‎ 图1 图2 图3 图4‎ ‎（2）性质探究：请完成凹四边形一个性质的证明．‎ ‎ 已知：如图2，四边形是凹四边形．‎ ‎ 求证：．‎ ‎（3）性质应用：‎ ‎ 如图3，在凹四边形中，的角平分线与的角平分线交于 ‎ 点，若，，则 ．‎ ‎（4）类比学习：‎ 如图4，在凹四边形中，点，，，分别是边，，，的中点，顺次连接各边中点得到四边形．若，，‎ 则四边形是 ．（填写序号即可）‎ A．梯形 B．菱形 C．矩形 D．正方形 朝阳一模 ‎26. 有这样一个问题：探究函数的图象与性质．‎ ‎ 小华根据学习函数的经验，对函数的图象与性质进行了探究.‎ 下面是小华的探究过程,请补充完整:‎ ‎(1)函数的自变量x的取值范围是 ；‎ ‎(2)下表是y与x的几组对应值.‎ x ‎…‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎…‎ y ‎…‎ ‎6‎ ‎6‎ m ‎…‎ ‎ 求m的值；‎ ‎（3）如下图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象；‎ ‎（4）结合函数的图象，写出该函数的一条性质： .‎ 门头沟二模 ‎26. 小鹏遇到这样一个问题，已知实数a、b（），请问是否有最小值，如果有请写出最小值并说明理由.‎ 他找不到思路，开始翻阅笔记，发现此题可以用以前老师讲的“配方”来解决 笔记中写到：求的最小值 步骤如下： ‎ ‎∵无论x取任意实数，‎ ‎∴的最小值是0‎ ‎（1）小鹏发现代数式可以用上面的方法找到最小值，请问最小值是多少，并说明理由；‎ ‎（2）小鹏通过笔记和问题（1）的方案很快解决了上面的问题，请你完成解答过程.‎ 西城二模 ‎ ‎ ‎26．学习了《平行四边形》一章以后，小东根据学习平行四边形的经验，对平行四边形的判定问题进行了再次探究．‎ 以下是小东的探究过程，请补充完整：‎ ‎（1）在四边形ABCD中，对角线AC与BD相交于点O．若AB∥CD，补充下列条件中能判断四边形 ABCD是平行四边形的是；（写出一个你认为正确选项的序号即可）；‎ ‎（A）BC＝AD（B）∠BAD=∠BCD（C） AO＝CO，‎ ‎（2）将（1）中的命题用文字语言表述为：‎ ①命题1；‎ ②画出图形，并写出命题1的证明过程；‎ ‎（3）小东进一步探究发现：‎ 若一个四边形ABCD的三个顶点A，B，C的位置如图所示，且这个四边形满足CD=AB，∠B=∠D，但四边形ABCD不是平行四边形，画出符合题意的四边形 ABCD，进而不东发现：命题2“一组对边相等，一组对角相等的四边形是平行四边形”是一个假命题．‎ 海淀二模 ‎26．已知y是x的函数，该函数的图象经过A（1，6），B（3，2）两点．‎ ‎（1）请写出一个符合要求的函数表达式；‎ ‎（2）若该函数的图象还经过点C（4，3），自变量x的取值范围是，该函数无最小值．‎ ‎①如图，在给定的坐标系xOy中，画出一个符合条件的函数的图象；‎ ‎②根据①中画出的函数图象，写出对应的函数值y约为；‎ ‎（3）写出（2）中函数的一条性质（题目中已给出的除外）．‎ 朝阳二模 ‎26. 下面是小东的探究学习过程，请补充完整：‎ ‎（1）探究函数（x＜1）的图象与性质．‎ 小东根据学习函数的经验，对函数（x＜1）的图象与性质进行了探究．‎ ‎①下表是y与x的几组对应值．‎ x ‎…‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎0‎ ‎…‎ y ‎…‎ ‎1‎ m ‎…‎ ‎ ‎ ‎ 求m的值；‎ ‎②如下图，在平面直角坐标系中，描出以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；‎ ‎ ‎ ‎③进一步探究发现，该函数图象的最高点的坐标是（0，1），结合函数的图象，写出该函数的其他性质（一条即可）： _____； ‎ ‎（2）小东在（1）的基础上继续探究：他将函数（x＜1）的图象向上平移1个单位长度，再向右平移1个单位长度后得到函数（x＜2）的图象，请写出函数（x＜2）的一条性质：_____.‎ 丰台二模 无 昌平二模 ‎26.有这样一个问题：探究函数的图象与性质，小静根据学习函数的经验，对函数的图象与性质进行了探究，下面是小静的探究过程，请补充完整：‎ ‎（1）函数的自变量x的取值范围是__________；‎ ‎（2）下表是y与x的几组对应值.‎ ‎…‎ ‎-1‎ ‎0‎ ‎1‎ ‎3‎ ‎4‎ ‎…‎ ‎…‎ ‎1‎ ‎4‎ m ‎1‎ ‎…‎ 表中的m=__________；‎ ‎（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；‎ ‎（4）结合函数图象，写出一条该函数图象的性质：______________________________.‎ 通州二模 ‎26．有这样一个问题：探究函数的图象与性质．‎ 小东根据学习函数的经验，对函数的图象与性质进行了探究．‎ 下面是小东的探究过程，请补充完整，并解决相关问题：‎ ‎（1）函数的自变量x的取值范围是　 　；‎ ‎（2）下表是y与x的几组对应值，求m的值；‎ x ‎…‎ ‎-4‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎…‎ m ‎…‎ ‎（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；‎ ‎（4）进一步探究发现，该函数图象在第二象限内的最低点的坐标是（-2，），结合函数的图象，写出该函数的其它性质（一条即可）　 ‎ ‎ 　．‎ ‎（5）根据函数图象估算方程 ‎ 的根为　 　　 ．（精 确到0.1）‎ 房山二模 ‎26.某班“数学兴趣小组”对函数的图象和性质进行了探究，探究过程如下，请补充完整：‎ ‎（1）自变量x的取值范围是；‎ x ‎…‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ y ‎…‎ ‎-2‎ ‎2‎ ‎…‎ ‎（2）下表是y与x的几组对应数值： ‎ 在平面直角坐标系中，描出了以表中各对对应值为坐标的点. 根据描出的点，画出该函数的图象；‎ ‎（3）进一步探究发现：该函数在第一象限内的最低点的坐标是（1，2）．观察函数图象，写出该函数的另一条性质；‎ ‎（4）请你利用配方法证明：当x＞0时，的最小值为2．‎ ‎（提示：当x＞0时，，）‎ 东城二模 ‎26. 佳佳想探究一元三次方程的解的情况. 根据以往的学习经验，他想到了方程与函数的关系：一次函数的图象与轴交点的横坐标即为一次方程的解；二次函数的图象与轴交点的横坐标即为一元二次方程的解. 如：二次函数的图象与轴的交点为和，交点的横坐标-1和3即为方程的解.‎ 根据以上方程与函数的关系，如果我们知道函数的图象与轴交点的横坐标，即可知道方程的解.‎ 佳佳为了解函数的图象，通过描点法画出函数的图象：‎ x ‎…‎ ‎…‎ y ‎…‎ ‎0‎ ‎0‎ ‎12‎ ‎…‎ ‎（1）直接写出m的值，并画出函数图象； ‎ ‎（2）根据表格和图象可知，方程的解有_____个，分别为__________________；‎ ‎（3）借助函数的图象，直接写出不等式的解集.‎ 石景山二模 ‎26．已知是的函数，下表是与的几组对应值．‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎ 小明根据学习函数的经验，利用上述表格所反映出的与之间的变化规律，对该函数的图象与性质进行了探究．‎ ‎ 下面是小明的探究过程，请补充完整：‎ ‎ （1）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点.根据 ‎ ‎ 描出的点，画出该函数的图象；‎ ‎ （2）根据画出的函数图象，写出：‎ ‎ ①对应的函数值约为 ；‎ ‎ ②该函数的一条性质： ．‎ 怀柔二模 ‎26. 某商品的进价为每件40元，当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查，每降价1元，每星期可多卖出20件，在确保盈利的前提下，解答下列问题：‎ ‎（1）若设每件降价x（x为整数）元，每星期售出商品的利润为y元，请写出x与y之间的函数关系式，并求出自变量x的取值范围；‎ ‎（2）请画出上述函数的大致图象.‎ ‎（3）当降价多少元时，每星期的利润最大？最大利润是多少？‎ 小丽解答过程如下：‎ 解：（1）根据题意，可列出表达式：‎ y=(60-x)(300+20x)-40(300+20x),‎ 即y=-20x2+100x+6000.‎ ‎∵降价要确保盈利，∴40＜60-x60.解得0x＜20.‎ ‎（2）上述表达式的图象是抛物线的一部分，函数的大致图象如图1：‎ ‎（3）∵a=-20＜0，‎ ‎∴当x==2.5时，y有最大值，y==6125.‎ 所以，当降价2.5元时，每星期的利润 最大，最大利润为6125.‎ 老师看了小丽的解题过程，说小马第（1）问的表达式是正确的，但自变量x的取值范围不准确.（2）（3）问的答案，也都存在问题.请你就老师说的问题，进行探究，写出你认为（1）（2）（3）中正确的答案，或说明错误原因.‎ 顺义二模 ‎26．阅读下列材料：‎ ‎ 实验数据显示，一般成人喝250毫升低度白酒后，其血液中酒精含量（毫克／百毫升）随时间的增加逐步增高达到峰值，之后血液中酒精含量随时间的增加逐渐降低．‎ 小明根据相关数据和学习函数的经验，对血液中酒精含量随时间变化的规律进行了探究，发现血液中酒精含量y是时间x的函数，其中y表示血液中酒精含量（毫克／百毫升），x表示饮酒后的时间（小时）.‎ ‎ 下表记录了6小时内11个时间点血液中酒精含量y(毫克／百毫升)随饮酒后的时间x（小时）（x>0）的变化情况：‎ 饮酒后的时间x ‎（小时）‎ ‎…‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎…‎ 血液中酒精含量y ‎（毫克／百毫升）‎ ‎…‎ ‎150‎ ‎200‎ ‎150‎ ‎45‎ ‎…‎ 下面是小明的探究过程，请补充完整：（1）如图，在平面直角坐标系xOy中，‎ 描出了上表中各对对应值为坐标的点，根据描出的点，画出血液中酒精含量y随 时间x变化的函数图象；‎ ‎（2）观察表中数据及图象可发现此函数图象在直线x=两侧可以用不同的函 数表达式表示，请你任选其中一部分写出表达式．‎ ‎（3）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克／百毫 升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员 晚上20∶00在家喝完250毫升低度白酒，第二天早上6∶30能否驾车去上 班?请说明理由．‎ 平谷二模 ‎26．小敏通过学习，知道了“在直角三角形中，30°的锐角所对的直角边等于斜边的一半”，她猜想这个命题的逆命题为“在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°”．为了证明这个命题的正确性，她画出了如图所示的图形．她又结合图形把这个命题理解为“在直角三角形ABC中，∠ACB=90°，直角边BC的长等于斜边AB长的一半时，BC所对的锐角∠A的度数等于30°”．请你根据小敏的图形和理解，补全已知和求证，并完成证明．‎ 已知：在Rt△ABC中，∠ACB=90°，____________________________．‎ 求证：_____________________________________ ．‎ 小敏把自己的猜想与数学小组的同学们进行了交流，经过充分交流、研讨，得出了以下两种想法：‎ 想法一：取AB中点D，连结CD，利用直角三角形斜边中线的性质使问题得到解决；‎ 想法二：沿AC翻折△ABC，得△ADC，构造特殊的三角形，使问题得到解决．‎ 请选择其中一种想法，帮助小敏完成解答过程．‎