- 2021-04-23 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江西省宜春市2012届高三数学上学期期末统考试卷 理 新人教A版
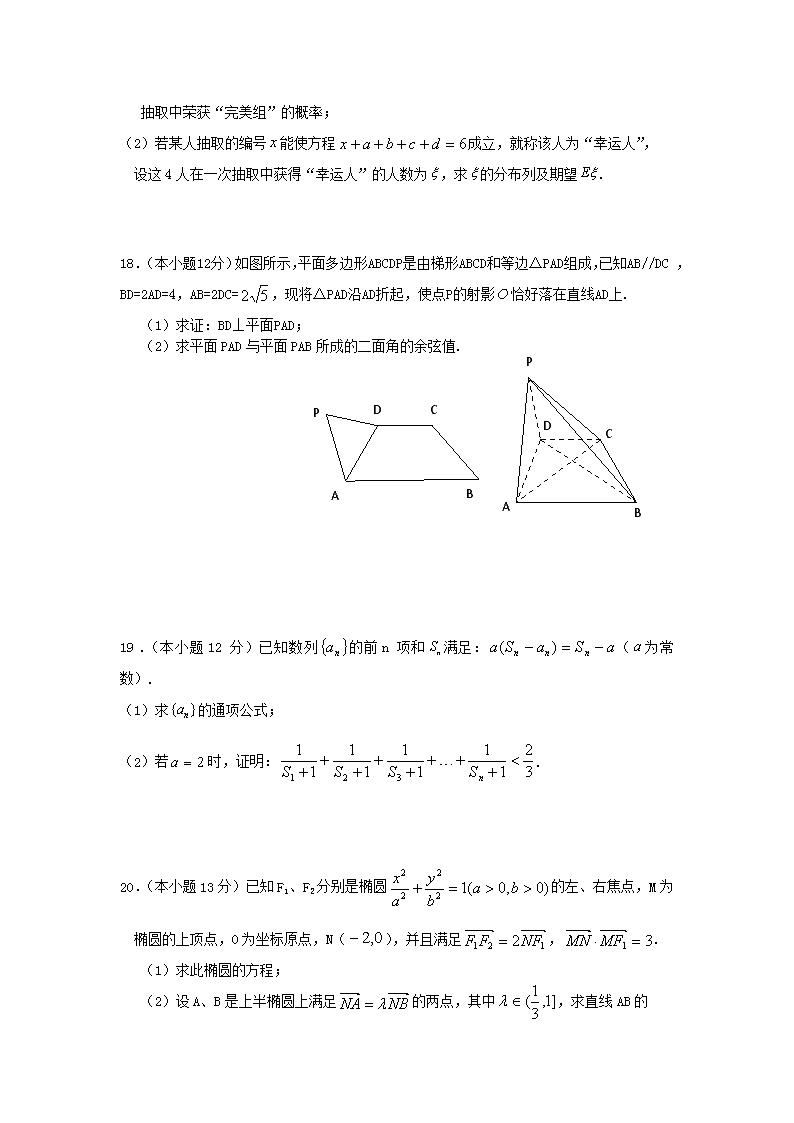
江西省宜春市2012届高三上学期期末统考试卷数学(理)试题 (注意:请将答案填在答题卡上) 一、选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中, 只有一项是符合题目要求的) 1. 已知集合A=﹛a, 3﹜,集合,且A∩B={0},若集合 S=A∪B,则S的真子集有 ( ). A.7个 B.8个 C.15个 D.16个 2.设,且(为虚数单位)为负实数,则m =( ) A. 2 B. 1 C. 0 D. -1 3.函数的零点所在区间为( ) A.(0,1) B.(1,2) C.(2,3) D.(3,+∞) 4.的展开式中常数项是( ) A. B.160 C.-160 D.-8 5.由直线,,y=0与曲线y=sinx所围成的封闭图形的面积为( ) A. 2- B.4- C. D. 6.已知,D是BC边上的一点,, 若记,则用表示所得的结果为( ) A. B. C. D. 7.函数取得最大值时的为( ) A. B. C. D.1 8.满足,若的最大值为7,则的最小值为( ) A. B.7 C. D.9 9.某几何体的主视图与左视图如图所示,则该几何体的俯视图可以是( ) 左视图 主视图 ② ① ③ ④ A.①②③ B. ②③④ C. ①②④ D. ①③④ 10.等差数列的前n项和为,已知,,则=( ) A.0 B.2011 C.4022 D. 二、填空题(本大题共5个小题,每小题5分,共25分,请把正确答案填在题中横线上) 第13题 11.3位教师分配到4个贫困村调查义务教育实施情况,若每个村 最多去人,则不同的分配方法种数是 .(用数字作答) 12.已知双曲线的两条渐近线均和圆C:x2+y2-6x+5=0相切, 且双曲线的右焦点为抛物线的焦点, 则该双曲线的标准方程为 . 13.右图给出的是计算的值的一个程序框图, 其中判断框内应填入关于的条件是 . 14.若存在使不等式+成立, 则实数的取值范围为 . 15.设函数的定义域为D,如果存在正实数,使对任意,都有, 且恒成立,则称函数为D上的“型增函数”.已知是 定义在R上的奇函数,且当时,,若为R上的 “2012型增函数”,则实数的取值范围是 . 三、解答题(本大题共6小题,共75分,解答写出必要的文字说明、演算过程及步骤) 16.(本小题12分)在⊿ABC中,角A、B、C所对应的边分别为 (1)若,,求A的值; (2)若,,求函数最小值. 17.(本小题12分)一个袋中装有4个形状大小完全相同的小球,球的编号分别为1、2、3、4,甲、乙、丙、丁依次有放回地随机抽取1个球 ,摸到球的编号分别为. (1)若四人抽取的编号数都不相同,则称这四人为“完美组” ,求这四人在一次 抽取中荣获“完美组”的概率; (2)若某人抽取的编号能使方程成立,就称该人为“幸运人”, 设这4人在一次抽取中获得“幸运人”的人数为,求的分布列及期望. 18.(本小题12分)如图所示,平面多边形ABCDP是由梯形ABCD和等边△PAD组成,已知AB//DC ,BD=2AD=4,AB=2DC=,现将△PAD沿AD折起,使点P的射影恰好落在直线AD上. (1)求证:BD⊥平面PAD; (2)B C P D A 求平面PAD与平面PAB所成的二面角的余弦值. P D C A B 19.(本小题12分)已知数列的前n项和满足:(为常数). (1)求的通项公式; (2)若时,证明:. 20.(本小题13分)已知F1、F2分别是椭圆的左、右焦点,M为 椭圆的上顶点,O为坐标原点,N(),并且满足,. (1)求此椭圆的方程; (2)设A、B是上半椭圆上满足的两点,其中,求直线AB的 斜率的取值范围. 21.(本小题满分14分)已知函数. (1)若函数在定义域内为增函数,求实数的取值范围; (2)设,若函数存在两个零点, 且满足,问:函数在处的切线能否平行于轴?若能, 求出该切线方程;若不能,请说明理由. 座位号 数学(理科)答题卡 一、选择题:(本大题共10小题,每小题5分,共50分) 题号 1 2 3 4 5 6 7 8 9 10 答案 二、填空题(本题共5小题,每小题5分,共25分) 11. ;12. ;13. ; 14. ;15. . 三、解答题(本大题共6小题,共75分,解答写出必要的文字说明,证明过程及演算步骤) 16、(本小题12分) 18.(12分)用下列任一条件代替(2),都可使所求得的椭圆方程仍为(※) ① 短半轴长为4; ② 离心率 e = ; ③ 右准线方程为 x = ; ④ 点P ( 3, ) 在椭圆上; ⑤ 椭圆上两点间的最大距离为10; …… 17、(本小题12分) 18、(本小题12分) B C P D A P D C A B 19、(本小题12分) 20、(本小题13分) 21、(本小题14分) 参考答案与评分标准 一、CDBCB,DAACB 二、11.60;12.;13.i >10(或或 );14.;15. 16.解:(Ⅰ)由得, 又由正弦定理,可得,………2分 , 又,………5分 (2) ,即 又 所以 ,即的最大值为16 …………7分 即 所以 , 又0<< 所以0< ……8分 …9分 因0<,所以<, …11分 ∴ ,当,…12分 17.解:(1)这四人在一次抽取中的基本事件有:种, 抽取的编号都不相同的基本事件有:种,故所求的概率…6分(2)可能取值为0,3,即摸到1且4人的和是5的有(1,1,1,2),(1,1,2,1), (1,2,1,1),(2,1,1,1),此时人数均为3; 而摸到2的且另3人的和是2不可能有,摸到3的且另3人的和是1不可能有, 摸到4的且另3人的和是-2不可能有,此时人数为0.…8分 P(=3)=4/256=1/64,P(=0)=252/256=63/64,…10分 0 3 P 63/64 1/64 =3/64.…12分 …11分 18.(1)证明:由题意知平面PAD⊥平面ABCD,又BD=2AD=4,AB=可得AB2=AD2+BD2, 则BD⊥AD,又AD为平面PAD与平面ABCD的交线,则BD⊥平面PAD;……6分 x B C P D A z y O (2)如图建立空间直角坐标,易知A(1,0,0), B(-1,4,0),P(0,0,), ,, 平面PDA的法向量为=(0,1,0), 设平面PAB的法向量为,由, 得, 故可取,则, 所以平面PAD与平面PAB所成的二面角的余弦值为.……12分 19.解:(1)当时∴,当时,由, 得相减得…3分 当时,…4分 当时,即是等比数列. ∴;…5分 综上:…6分 (2)若时,, ………8分 设, 则 …10分 ……12分 20.解:(1)由,,M(0,b),F1(-c,0),F2(c,0) , 从而所求椭圆的方程为………………6分 (2)三点共线,而点N的坐标为(-2,0). 设直线AB的方程为,其中k为直线AB的斜率,依条件知k≠0. 由消去x得,即 根据条件可知 且解得………8分 设,则根据韦达定理,得 又由 从而 消去 令,则 由于 ,在上的减函数, 从而,即, 又 , 因此直线AB的斜率的取值范围是………………13分 21.解:(1) 由题意,知恒成立,即. …… 3分 又,当且仅当时等号成立. 故,所以. ……6分 (2)设在的切线平行于轴,其中 ① ② ③④ 结合题意,有 ……9分 ①—②得 所以由④得 所以⑤ ……11分 设,⑤式变为 设, 所以函数在上单调递增, 因此,,即 也就是,,此式与⑤矛盾. 所以在处的切线不能平行于轴. ……14分查看更多