高中数学分章节训练试题：39立体几何与空间向量1

高中数学分章节训练试题：39立体几何与空间向量1

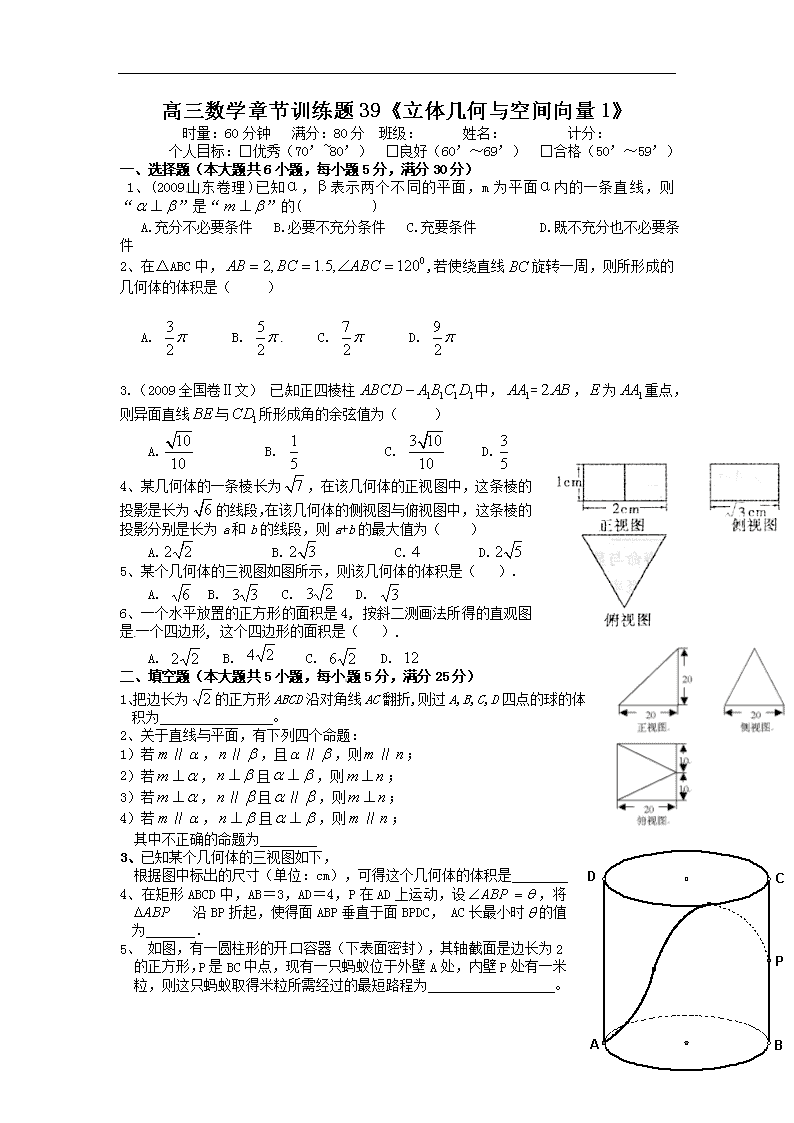
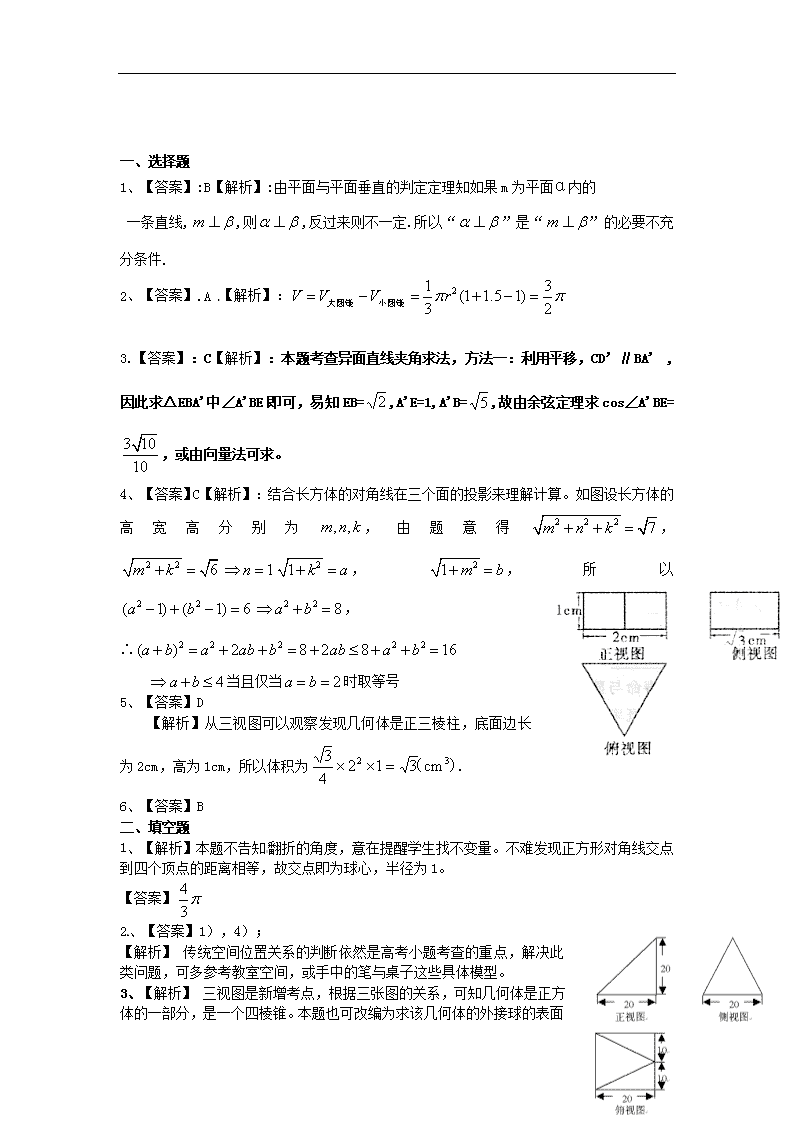
高三数学章节训练题39《立体几何与空间向量1》‎ 时量：60分钟 满分：80分 班级： 姓名： 计分：‎ ‎ 个人目标：□优秀（‎70’‎~‎80’‎） □良好（‎60’‎～‎69’‎） □合格（‎50’‎～‎59’‎）‎ 一、选择题（本大题共6小题，每小题5分，满分30分）‎ ‎1、(2009山东卷理)已知α，β表示两个不同的平面，m为平面α内的一条直线，则“”是“”的( )‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎2、在△ABC中，,若使绕直线旋转一周，则所形成的几何体的体积是（ ）‎ A. B. C. D. ‎ ‎3.（2009全国卷Ⅱ文） 已知正四棱柱中，=，为重点，则异面直线与所形成角的余弦值为（ ）‎ A. B. C. D. ‎ ‎4、某几何体的一条棱长为，在该几何体的正视图中，这条棱的投影是长为的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a+b的最大值为（ ）‎ A.　 B. 　C.　 D. ‎ ‎5、某个几何体的三视图如图所示，则该几何体的体积是（ ）. ‎ A. B. C. D. ‎ ‎6、一个水平放置的正方形的面积是4, 按斜二测画法所得的直观图是一个四边形, 这个四边形的面积是（ ）.‎ A. B. C. D. ‎ 二、填空题（本大题共5小题，每小题5分，满分25分）‎ ‎1、把边长为的正方形ABCD沿对角线AC翻折,则过A,B,C,D四点的球的体 积为 。‎ ‎2、关于直线与平面，有下列四个命题：‎ ‎1）若∥，∥，且∥，则∥；‎ ‎2）若，且，则；‎ ‎3）若，∥且∥，则；‎ ‎4）若∥，且，则∥；‎ 其中不正确的命题为 ‎ ‎3、已知某个几何体的三视图如下，‎ 根据图中标出的尺寸（单位：cm），可得这个几何体的体积是 ‎ ‎4、在矩形ABCD中，AB＝3，AD＝4，P在AD上运动，设，将 沿BP折起，使得面ABP垂直于面BPDC， AC长最小时的值为 ． ‎ ‎5、 如图，有一圆柱形的开口容器（下表面密封），其轴截面是边长为2的正方形，P是BC中点，现有一只蚂蚁位于外壁A处，内壁P处有一米粒，则这只蚂蚁取得米粒所需经过的最短路程为 。‎ 三、解答题：（本大题共2小题，满分25分）‎ A B C A1‎ B1‎ C1‎ ‎1、（2009广东东莞）在直三棱柱中，，，且异面直线与所成的角等于，设.（1）求的值；（2）求平面与平面所成的锐二面角的大小.‎ ‎2. 如图，在三棱锥中，，，． ‎ ‎（Ⅰ）求证：；（Ⅱ）求二面角的余弦值；（Ⅲ）求点到平面的距离．‎ A C B D P 一、选择题 ‎1、【答案】:B【解析】:由平面与平面垂直的判定定理知如果m为平面α内的 一条直线,,则,反过来则不一定.所以“”是“”的必要不充分条件. ‎ ‎2、【答案】.A 【解析】：‎ ‎3.【答案】：C【解析】：本题考查异面直线夹角求法，方法一：利用平移，CD’∥BA',因此求△EBA'中∠A'BE即可，易知EB=,A'E=1,A'B=,故由余弦定理求cos∠A'BE=，或由向量法可求。‎ ‎4、【答案】C【解析】：结合长方体的对角线在三个面的投影来理解计算。如图设长方体的高宽高分别为，由题意得， ，，所以，‎ 当且仅当时取等号 ‎5、【答案】D ‎【解析】从三视图可以观察发现几何体是正三棱柱，底面边长为2cm，高为1cm，所以体积为.‎ ‎6、【答案】B 二、填空题 ‎1、【解析】本题不告知翻折的角度，意在提醒学生找不变量。不难发现正方形对角线交点到四个顶点的距离相等，故交点即为球心，半径为1。‎ ‎【答案】‎ ‎2、【答案】1），4）； ‎ ‎【解析】 传统空间位置关系的判断依然是高考小题考查的重点，解决此类问题，可多参考教室空间，或手中的笔与桌子这些具体模型。‎ ‎3、【解析】 三视图是新增考点，根据三张图的关系，可知几何体是正方体的一部分，是一个四棱锥。本题也可改编为求该几何体的外接球的表面积，则必须补全为正方体，增加了难度。‎ ‎【答案】‎ ‎4、【解析】本题是立体几何中的最值问题，建立数学模型，用函数解决是一种重要方法。过A作AHBP于H，连CH，‎ ‎∴．∴．‎ 在， ‎ ‎∴在，，∴时，AC长最小；‎ ‎【答案】‎ ‎5、 【解析】此类求曲面上最短路程问题通常考虑侧面展开。侧面展开后得矩形，其中问题转化为在上找一点使最短作关于的对称点，连接，令与交于点则得 的最小值为 ‎【答案】‎ 三、填空题 解法一：（1），‎ 就是异面直线与所成的角，‎ 即，……（2分）‎ 连接，又，则 为等边三角形，……………………………4分 由，，‎ ‎；………6分 ‎（2）取的中点，连接，过作于，连接，‎ ‎,平面 ‎ ………………8分 又，所以平面，即，‎ 所以就是平面与平面所成的锐二面角的平面角。…………10分 在中，，，,‎ ‎，…………………………13分 因此平面与平面所成的锐二面角的大小为。…………14分 说明：取的中点，连接，…………同样给分（也给10分）‎ 解法二：（1）建立如图坐标系，于是，，，（）‎ A1‎ B C B1‎ C1‎ x y z ‎，， …………3分 由于异面直线与所成的角，‎ 所以与的夹角为 即 ‎………6分 ‎ ‎ ‎（2）设向量且平面 于是且，即且， ‎ 又，，所以，不妨设……8分 ‎ 同理得，使平面，（10分）‎ 设与的夹角为，所以依，‎ ‎，………………12分 平面，平面，‎ 因此平面与平面所成的锐二面角的大小为。…………14分 说明：或者取的中点，连接，于是显然平面 ‎2. 解法一：（Ⅰ）取中点，连结．，．，．‎ ‎，平面．平面，．‎ ‎（Ⅱ），，．又，．‎ 又，即，且，平面．取中点．连结．‎ A C B E P A C B D P H ‎，．是在平面内的射影，．‎ 是二面角的平面角．在中，，，，． ‎ ‎（Ⅲ）由（Ⅰ）知平面，平面平面．过作，垂足为．‎ 平面平面，平面．的长即为点到平面的距离．‎ 由（Ⅰ）知，又，且，平面．平面，．在中，，，‎ ‎．． 点到平面的距离为． ‎ ‎ ‎ ‎ ‎ 网解法二：（Ⅰ），，．又，‎ ‎．，平面．平面，．‎ ‎（Ⅱ）如图，以为原点建立空间直角坐标系．则．‎ 设．，，．取中点，连结．‎ ‎，，，．是二面角的平面角．‎ ‎，，， ‎ A C B P z x y H E ‎． ‎ ‎ ‎ ‎（Ⅲ），在平面内的射影为正的中心，且的长为点到平面的距离．‎ 如（Ⅱ）建立空间直角坐标系．，点的坐标为．．中学学点到平面的距离为．‎