- 2021-04-23 发布 |
- 37.5 KB |
- 174页

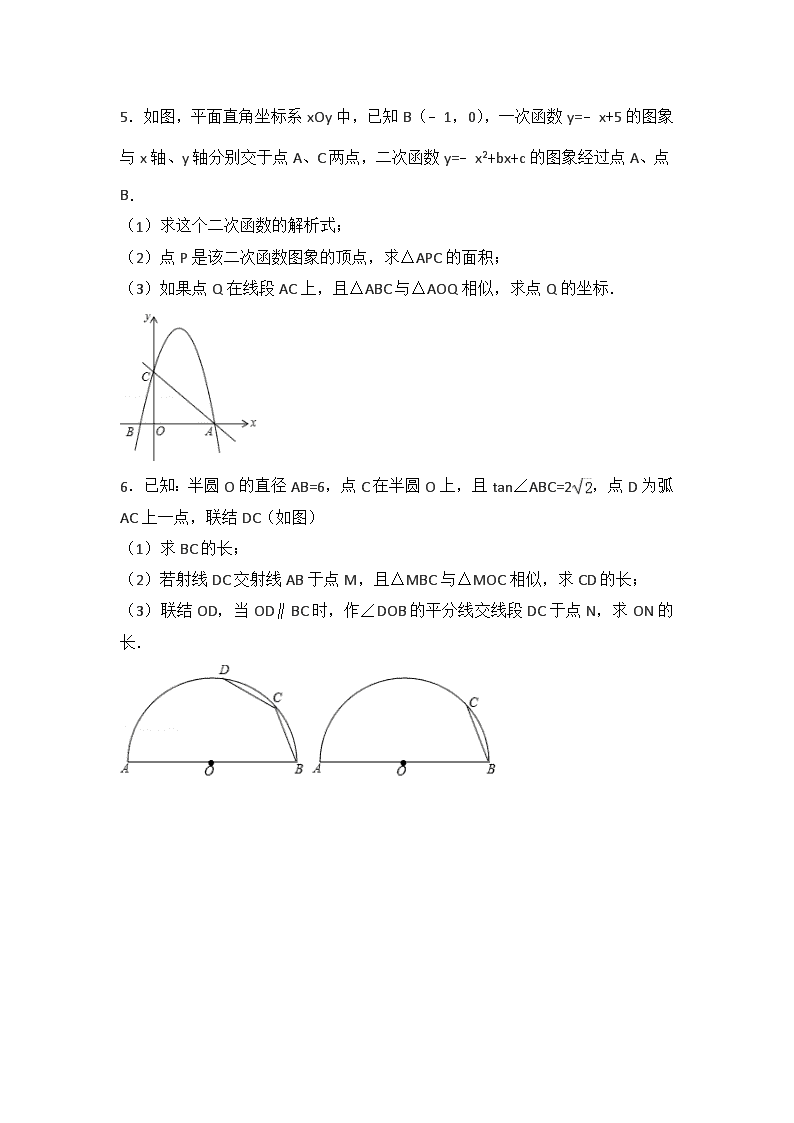
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学挑战压轴题含答案
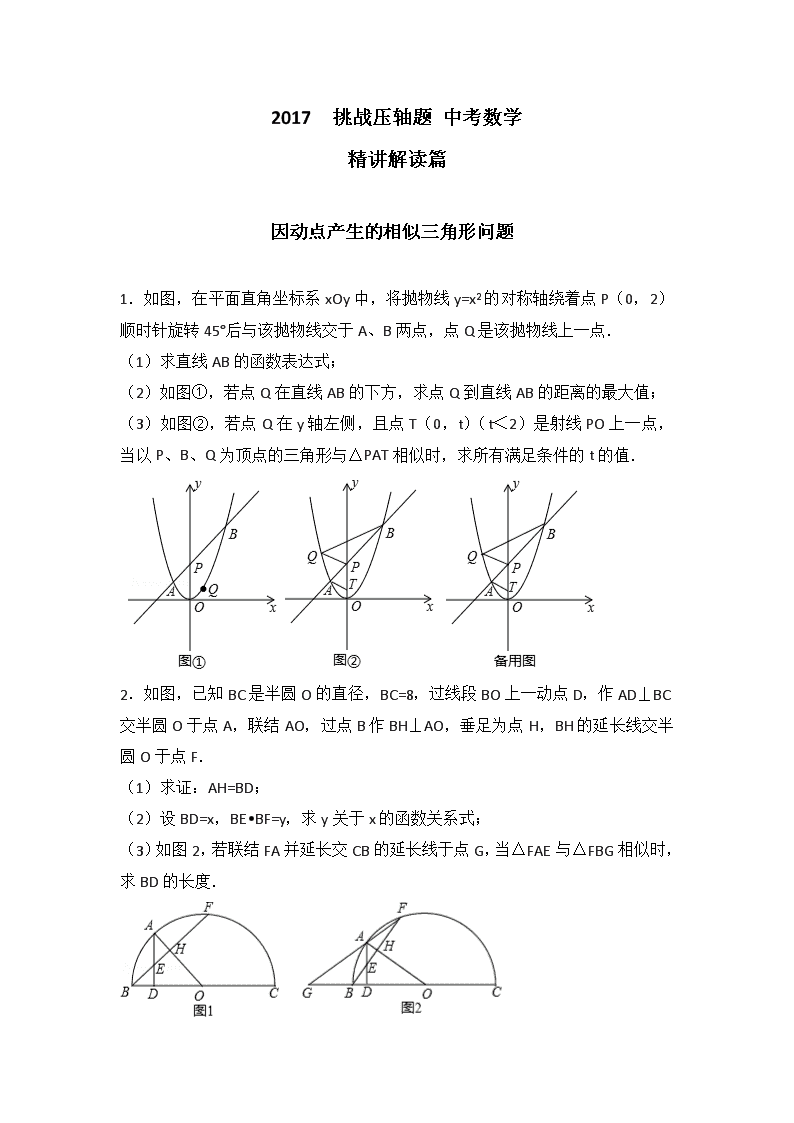
2017 挑战压轴题 中考数学 精讲解读篇 因动点产生的相似三角形问题 1.如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P(0,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点. (1)求直线AB的函数表达式; (2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值; (3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是射线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值. 2.如图,已知BC是半圆O的直径,BC=8,过线段BO上一动点D,作AD⊥BC交半圆O于点A,联结AO,过点B作BH⊥AO,垂足为点H,BH的延长线交半圆O于点F. (1)求证:AH=BD; (2)设BD=x,BE•BF=y,求y关于x的函数关系式; (3)如图2,若联结FA并延长交CB的延长线于点G,当△FAE与△FBG相似时,求BD的长度. 3.如图,在平面直角坐标系xOy中,直线AB过点A(3,0)、B(0,m)(m>0),tan∠BAO=2. (1)求直线AB的表达式; (2)反比例函数y=的图象与直线AB交于第一象限内的C、D两点(BD<BC),当AD=2DB时,求k1的值; (3)设线段AB的中点为E,过点E作x轴的垂线,垂足为点M,交反比例函数y=的图象于点F,分别联结OE、OF,当△OEF∽△OBE时,请直接写出满足条件的所有k2的值. 4.如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G. (1)当点E是BD的中点时,求tan∠AFB的值; (2)CE•AF的值是否随线段AD长度的改变而变化?如果不变,求出CE•AF的值;如果变化,请说明理由; (3)当△BGE和△BAF相似时,求线段AF的长. 5.如图,平面直角坐标系xOy中,已知B(﹣1,0),一次函数y=﹣x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=﹣x2+bx+c的图象经过点A、点B. (1)求这个二次函数的解析式; (2)点P是该二次函数图象的顶点,求△APC的面积; (3)如果点Q在线段AC上,且△ABC与△AOQ相似,求点Q的坐标. 6.已知:半圆O的直径AB=6,点C在半圆O上,且tan∠ABC=2,点D为弧AC上一点,联结DC(如图) (1)求BC的长; (2)若射线DC交射线AB于点M,且△MBC与△MOC相似,求CD的长; (3)联结OD,当OD∥BC时,作∠DOB的平分线交线段DC于点N,求ON的长. 7.如图,已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(3,﹣1),点C(0,﹣4),顶点为点M,过点A作AB∥x轴,交y轴与点D,交该二次函数图象于点B,连结BC. (1)求该二次函数的解析式及点M的坐标; (2)若将该二次函数图象向上平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包含△ABC的边界),求m的取值范围; (3)点P时直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程). 因动点产生的等腰三角形问题 8.如图1,在△ABC中,∠ACB=90°,∠BAC=60°,点E是∠BAC角平分线上一点,过点E作AE的垂线,过点A作AB的垂线,两垂线交于点D,连接DB,点F是BD的中点,DH⊥AC,垂足为H,连接EF,HF. (1)如图1,若点H是AC的中点,AC=2,求AB,BD的长; (2)如图1,求证:HF=EF; (3)如图2,连接CF,CE.猜想:△CEF是否是等边三角形?若是,请证明;若不是,说明理由. 9.已知,一条抛物线的顶点为E(﹣1,4),且过点A(﹣3,0),与y轴交于点C,点D是这条抛物线上一点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴,垂足为K,DK分别交线段AE、AC于点G、H. (1)求这条抛物线的解析式; (2)求证:GH=HK; (3)当△CGH是等腰三角形时,求m的值. 10.如图,已知在Rt△ABC中,∠ACB=90°,AB=5,sinA=,点P是边BC上的一点,PE⊥AB,垂足为E,以点P为圆心,PC为半径的圆与射线PE相交于点Q,线段CQ与边AB交于点D. (1)求AD的长; (2)设CP=x,△PCQ的面积为y,求y关于x的函数解析式,并写出定义域; (3)过点C作CF⊥AB,垂足为F,联结PF、QF,如果△PQF是以PF为腰的等腰三角形,求CP的长. 11.如图(1),直线y=﹣x+n交x轴于点A,交y轴于点C(0,4),抛物线y=x2+bx+c经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m. (1)求抛物线的解析式; (2)当△BDP为等腰直角三角形时,求线段PD的长; (3)如图(2),将△BDP绕点B逆时针旋转,得到△BD′P′,当旋转角∠PBP′=∠OAC,且点P的对应点P′落在坐标轴上时,请直接写出点P的坐标. 12.综合与探究 如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8). (1)求抛物线的函数表达式,并分别求出点B和点E的坐标; (2)试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由; (3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形. 因动点产生的直角三角形问题 13.已知,如图1,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=11,CD=6,tan∠ABC=2,点E在AD边上,且AE=3ED,EF∥AB交BC于点F,点M、N分别在射线FE和线段CD上. (1)求线段CF的长; (2)如图2,当点M在线段FE上,且AM⊥MN,设FM•cos∠EFC=x,CN=y,求y关于x的函数解析式,并写出它的定义域; (3)如果△AMN为等腰直角三角形,求线段FM的长. 14.如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3. (1)分别求直线l1与x轴,直线l2与AB的交点坐标; (2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标; (3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由). 因动点产生的平行四边形问题 15.如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC. (1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示); (2)点E是直线l上方的抛物线上的一点,若△ACE的面积的最大值为,求a的值; (3)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由. 16.如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△ BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系. (1)求点E坐标及经过O,D,C三点的抛物线的解析式; (2)一动点P从点C出发,沿CB以每秒2 个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ; (3)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点的坐标;若不存在,请说明理由. 17.如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D和点C关于抛物线的对称轴对称,直线AD与y轴交于点E. (1)求直线AD的解析式; (2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值; (3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是以AM为边的矩形.若点T和点Q关于AM所在直线对称,求点T的坐标. 18.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=CD,以DE,DF为邻边作矩形DEGF.设AQ=3x. (1)用关于x的代数式表示BQ,DF. (2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长. (3)在点P的整个运动过程中, ①当AP为何值时,矩形DEGF是正方形? ②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案). 19.在平面直角坐标系xOy(如图)中,经过点A(﹣1,0)的抛物线y=﹣x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称. (1)求b的值以及直线AD与x轴正方向的夹角; (2)如果点E是抛物线上一动点,过E作EF平行于x轴交直线AD于点F,且F在E的右边,过点E作EG⊥AD与点G,设E的横坐标为m,△EFG的周长为l,试用m表示l; (3)点M是该抛物线的顶点,点P是y轴上一点,Q是坐标平面内一点,如果以点A、M、P、Q为顶点的四边形是矩形,求该矩形的顶点Q的坐标. 20.如图,直线y=mx+4与反比例函数y=(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2. (1)求反比例函数解析式; (2)联结BO,求∠DBO的正切值; (3)点M在直线x=﹣1上,点N在反比例函数图象上,如果以点A、B、M、N为顶点的四边形是平行四边形,求点N的坐标. 21.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B. (1)求二次函数y=ax2+bx+c的表达式; (2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积; (3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标. 因动点产生的梯形问题 22.如图,在平面直角坐标系xOy中,二次函数y=+bx+c的图象与y轴交于点A,与双曲线y=有一个公共点B,它的横坐标为4,过点B作直线l∥x轴,与该二次函数图象交于另一个点C,直线AC在y轴上的截距是﹣6. (1)求二次函数的解析式; (2)求直线AC的表达式; (3)平面内是否存在点D,使A、B、C、D为顶点的四边形是等腰梯形?如果存在,求出点D坐标;如果不存在,说明理由. 23.如图,矩形OMPN的顶点O在原点,M、N分别在x轴和y轴的正半轴上,OM=6,ON=3,反比例函数y=的图象与PN交于C,与PM交于D,过点C作CA⊥x轴于点A,过点D作DB⊥y轴于点B,AC与BD交于点G. (1)求证:AB∥CD; (2)在直角坐标平面内是否若存在点E,使以B、C、D、E为顶点,BC为腰的梯形是等腰梯形?若存在,求点E的坐标;若不存在请说明理由. 因动点产生的面积问题 24.如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含端点),过点P作PF⊥BC于点F,点D、E的坐标分别为(0,6),(﹣4,0),连接PD、PE、DE. (1)请直接写出抛物线的解析式; (2)小明探究点P的位置发现:当P与点A或点C重合时,PD与PF的差为定值,进而猜想:对于任意一点P,PD与PF的差为定值,请你判断该猜想是否正确,并说明理由; (3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE周长最小时“好点”的坐标. 25.如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥ CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t. (1)求点M的坐标(用含t的代数式表示). (2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由. (3)当t为何值时,四边形BNDM的面积最小. 26.在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上. (1)小明发现DG⊥BE,请你帮他说明理由. (2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长. (3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由. 27.在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C. (1)求过A,B,C三点的抛物线的解析式; (2)P为抛物线上一点,它关于原点的对称点为Q. ①当四边形PBQC为菱形时,求点P的坐标; ②若点P的横坐标为t(﹣1<t< 1),当t为何值时,四边形PBQC面积最大?并说明理由. 28.如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点. (1)∠OBA= °. (2)求抛物线的函数表达式. (3)若P为抛物线上位于第一象限内的一个动点,以P、O、A、E为顶点的四边形面积记作S,则S取何值时,相应的点P有且只有3个? 29.如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上. (1)求抛物线的解析式; (2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由; (3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由. 30.已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B (1)求m的取值范围; (2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标; (3)当<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值. 31.问题提出 (1)如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形. 问题探究 (2)如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由. 问题解决 (3)如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG= 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由. 32.如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y=x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K. (1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处. ①点B的坐标为( 、 ),BK的长是 ,CK的长是 ; ②求点F的坐标; ③请直接写出抛物线的函数表达式; (2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1•S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值. 温馨提示:考生可以根据题意,在备用图中补充图形,以便作答. 33.如图,已知▱ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作▱ABCD关于直线AD的对称图形AB1C1D (1)若m=3,试求四边形CC1B1B面积S的最大值; (2)若点B1恰好落在y轴上,试求的值. 因动点产生的相切问题 34.如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l. (1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标; (2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线l的对称点为N,试证明四边形CDAN是平行四边形; (3)点P在直线l上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标. 35.如图,在Rt△ABC中,∠C=90°,AC=14,tanA=,点D是边AC上一点,AD=8,点E是边AB上一点,以点E为圆心,EA为半径作圆,经过点D,点F是边AC上一动点(点F不与A、C重合),作FG⊥EF,交射线BC于点G. (1)用直尺圆规作出圆心E,并求圆E的半径长(保留作图痕迹); (2)当点G的边BC上时,设AF=x,CG=y,求y关于x的函数解析式,并写出它的定义域; (3)联结EG,当△EFG与△FCG相似时,推理判断以点G为圆心、CG为半径的圆G与圆E可能产生的各种位置关系. 36.如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°. 点C是弧AB上的点,联结PC、DC. (1)联结BD交弧AB于E,当a=2时,求BE的长; (2)当以PC为半径的⊙P和以CD为半径的⊙C相切时,求a的值; (3)当直线DC经过点B,且满足PC•OA=BC•OP时,求扇形OAB的半径长. 37.如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<). (1)如图1,连接DQ平分∠BDC时,t的值为 ; (2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值; (3)请你继续进行探究,并解答下列问题: ①证明:在运动过程中,点O始终在QM所在直线的左侧; ②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由. 38.如图,抛物线y=﹣x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧. (1)求抛物线的解析式; (2)若PA:PB=3:1,求一次函数的解析式; (3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得⊙C同时与x轴和直线AP都相切,如果存在,请求出点C的坐标,如果不存在,请说明理由. 因动点产生的线段和差问题 39.如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q. (1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 ; (2)若两个三角形面积满足S△POQ=S△PAQ,求m的值; (3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD•DQ的最大值. 40.抛物线y=ax2+bx+4(a≠0)过点A(1,﹣1),B(5,﹣1),与y轴交于点C. (1)求抛物线的函数表达式; (2)如图1,连接CB,以CB为边作▱CBPQ,若点P在直线BC上方的抛物线上,Q为坐标平面内的一点,且▱CBPQ的面积为30,求点P的坐标; (3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值. 41.如图,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12. (1)如图①,点M是四边形ABCD边AD上的一点,则△BMC的面积为 ; (2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△ BNC周长的最小值; (3)如图③,在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由. 42.如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4,∠BAD=60°,且AB>4. (1)求∠EPF的大小; (2)若AP=6,求AE+AF的值; (3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值. 43.如图,在平面直角坐标系中,抛物线y=﹣x2﹣x+2与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D. (1)填空:点A的坐标为( , ),点B的坐标为( , ),点C的坐标为( , ),点D的坐标为( , ); (2)点P是线段BC上的动点(点P不与点B、C重合) ①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标; ②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长; ③若点Q是线段AB上的动点(点Q不与点A、B重合),点R是线段AC上的动点(点R不与点A、C重合),请直接写出△PQR周长的最小值. 44.如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM. (1)当AN平分∠MAB时,求DM的长; (2)连接BN,当DM=1时,求△ABN的面积; (3)当射线BN交线段CD于点F时,求DF的最大值. 45.如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在上且不与A点重合,但Q点可与B点重合. 发现:的长与的长之和为定值l,求l: 思考:点M与AB的最大距离为 ,此时点P,A间的距离为 ; 点M与AB的最小距离为 ,此时半圆M的弧与AB所围成的封闭图形面积为 ; 探究:当半圆M与AB相切时,求的长. (注:结果保留π,cos35°=,cos55°=) 46.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b. 填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示) (2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE. ①请找出图中与BE相等的线段,并说明理由; ②直接写出线段BE长的最大值. (3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标. 47.如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B. (1)求该抛物线的函数表达式; (2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值; (3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′. ①写出点M′的坐标; ②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数). 48.如图,在平面直角坐标系xOy中,将二次函数y=x2﹣1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N. (1)求N的函数表达式; (2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值; (3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数. 49.如图,顶点为A(,1)的抛物线经过坐标原点O,与x轴交于点B. (1)求抛物线对应的二次函数的表达式; (2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB; (3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标. 2017 挑战压轴题 中考数学 精讲解读篇 参考答案与试题解析 一.解答题(共36小题) 1.如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P(0,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点. (1)求直线AB的函数表达式; (2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值; (3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是射线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值. 【分析】(1)根据题意易得点M、P的坐标,利用待定系数法来求直线AB的解析式; (2)如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,构建等腰直角△QDC,利用二次函数图象上点的坐标特征和二次函数最值的求法进行解答; (3)根据相似三角形的对应角相等推知:△PBQ中必有一个内角为45°;需要分类讨论:∠PBQ=45°和∠PQB=45°;然后对这两种情况下的△PAT是否是直角三角形分别进行解答.另外,以P、B、Q为顶点的三角形与△PAT相似也有两种情况:△Q″PB∽△PAT、△Q″BP∽△PAT. 【解答】解:(1)如图①,设直线AB与x轴的交点为M. ∵∠OPA=45°, ∴OM=OP=2,即M(﹣2,0). 设直线AB的解析式为y=kx+b(k≠0),将M(﹣2,0),P(0,2)两点坐标代入,得 , 解得. 故直线AB的解析式为y=x+2; (2)如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,根据条件可知△QDC为等腰直角三角形,则QD=QC. 设Q(m,m2),则C(m,m+2). ∴QC=m+2﹣m2=﹣(m﹣)2+, QD=QC=[﹣(m﹣)2+]. 故当m=时,点Q到直线AB的距离最大,最大值为; (3)∵∠APT=45°, ∴△PBQ中必有一个内角为45°,由图知,∠BPQ=45°不合题意. ①如图②,若∠PBQ=45°,过点B作x轴的平行线,与抛物线和y轴分别交于点Q′、F.此时满足∠PBQ′=45°. ∵Q′(﹣2,4),F(0,4), ∴此时△BPQ′是等腰直角三角形,由题意知△PAT也是等腰直角三角形. (i)当∠PTA=90°时,得到:PT=AT=1,此时t=1; (ii)当∠PAT=90°时,得到:PT=2,此时t=0. ②如图③,若∠PQB=45°,①中是情况之一,答案同上; 先以点F为圆心,FB为半径作圆,则P、B、Q′都在圆F上,设圆F与y轴左侧的抛物线交于另一点Q″. 则∠PQ″B=∠PQ′B=45°(同弧所对的圆周角相等),即这里的交点Q″也是符合要求. 设Q″(n,n2)(﹣2<n<0),由FQ″=2,得 n2+(4﹣n2)2=22,即n4﹣7n2+12=0. 解得n2=3或n2=4,而﹣2<n<0,故n=﹣,即Q″(﹣,3). 可证△PFQ″为等边三角形, 所以∠PFQ″=60°,又PQ″=PQ″, 所以∠PBQ″=∠PFQ″=30°. 则在△PQ″B中,∠PQ″B=45°,∠PBQ″=30°. (i)若△Q″PB∽△PAT,则过点A作y轴的垂线,垂足为E. 则ET=AE=,OE=1, 所以OT=﹣1, 解得t=1﹣; (ii)若△Q″BP∽△PAT,则过点T作直线AB垂线,垂足为G. 设TG=a,则PG=TG=a,AG=TG=a,AP=, ∴a+a=, 解得PT=a=﹣1, ∴OT=OP﹣PT=3﹣, ∴t=3﹣. 综上所述,所求的t的值为t=1或t=0或t=1﹣或t=3﹣. 2.如图,已知BC是半圆O的直径,BC=8,过线段BO上一动点D,作AD⊥BC交半圆O于点A,联结AO,过点B作BH⊥AO,垂足为点H,BH的延长线交半圆O于点F. (1)求证:AH=BD; (2)设BD=x,BE•BF=y,求y关于x的函数关系式; (3)如图2,若联结FA并延长交CB的延长线于点G,当△FAE与△FBG相似时,求BD的长度. 【分析】(1)由AD⊥BC,BH⊥AO,利用垂直的定义得到一对直角相等,再由一对公共角,且半径相等,利用AAS得到三角形ADO与三角形BHO全等,利用全等三角形对应边相等得到OH=OD,利用等式的性质化简即可得证; (2)连接AB,AF,如图1所示,利用HL得到直角三角形ADB与直角三角形BHA全等,利用全等三角形对应角相等得到一对角相等,再由公共角相等得到三角形ABE与三角形AFB相似,由相似得比例即可确定出y与x的函数解析式; (3)连接OF,如图2所示,利用两对角相等的三角形相似得到三角形AFO与三角形FOG相似,由相似得比例求出BD的长即可. 【解答】(1)证明:∵AD⊥BC,BH⊥AO, ∴∠ADO=∠BHO=90°, 在△ADO与△BHO中, , ∴△ADO≌△BHO(AAS), ∴OH=OD, 又∵OA=OB, ∴AH=BD; (2)解:连接AB、AF,如图1所示, ∵AO是半径,AO⊥弦BF, ∴∴AB=AF, ∴∠ABF=∠AFB, 在Rt△ADB与Rt△BHA中, , ∴Rt△ADB≌Rt△BHA(HL), ∴∠ABF=∠BAD, ∴∠BAD=∠AFB, 又∵∠ABF=∠EBA, ∴△BEA∽△BAF, ∴=, ∴BA2=BE•BF, ∵BE•BF=y, ∴y=BA2, ∵∠ADO=∠ADB=90°, ∴AD2=AO2﹣DO2,AD2=AB2﹣BD2, ∴AO2﹣DO2=AB2﹣BD2, ∵直径BC=8,BD=x, ∴AB2=8x, 则y=8x(0<x<4); 方法二:∵BE•BF=y,BF=2BH, ∴BE•BH=y, ∵△BED∽△BOH, ∴=, ∴OB•BD=BE•BH, ∴4x=y, ∴y=8x(0<x<4); (3)解:连接OF,如图2所示, ∵∠GFB是公共角,∠FAE>∠G, ∴当△FAE∽△FBG时,∠AEF=∠G, ∵∠BHA=∠ADO=90°, ∴∠AEF+∠DAO=90°,∠AOD+∠DAO=90°, ∴∠AEF=∠AOD, ∴∠G=∠AOD, ∴AG=AO=4, ∵∴∠AOD=∠AOF, ∴∠G=∠AOF, 又∵∠GFO是公共角, ∴△FAO∽△FOG, ∴=, ∵AB2=8x,AB=AF, ∴AF=2x, ∴=, 解得:x=3±, ∵3+>4,舍去, ∴BD=3﹣. 3.如图,在平面直角坐标系xOy中,直线AB过点A(3,0)、B(0,m)(m>0),tan∠BAO=2. (1)求直线AB的表达式; (2)反比例函数y=的图象与直线AB交于第一象限内的C、D两点(BD<BC),当AD=2DB时,求k1的值; (3)设线段AB的中点为E,过点E作x轴的垂线,垂足为点M,交反比例函数y=的图象于点F,分别联结OE、OF,当△OEF∽△OBE时,请直接写出满足条件的所有k2的值. 【分析】(1)先通过解直角三角形求得A的坐标,然后根据待定系数法即可求得直线AB的解析式; (2)作DE∥OA,根据题意得出== ,求得DE,即D的横坐标,代入AB的解析式求得纵坐标,然后根据反比例函数图象上点的坐标特征即可求得k1; (3)根据勾股定理求得AB、OE,进一步求得BE,然后根据相似三角形的性质求得EF的长,从而求得FM的长,得出F的坐标,然后根据反比例函数图象上点的坐标特征即可求得k2. 【解答】解:(1)∵A(3,0)、B(0,m)(m>0), ∴OA=3,OB=m, ∵tan∠BAO==2, ∴m=6, 设直线AB的解析式为y=kx+b, 代入A(3,0)、B(0,6)得: 解得:b=6,k=﹣2 ∴直线AB的解析式为y=﹣2x+6; (2)如图1,∵AD=2DB, ∴=, 作DE∥OA, ∴==, ∴DE=OA=1, ∴D的横坐标为1, 代入y=﹣2x+6得,y=4, ∴D(1,4), ∴k1=1×4=4; (3)如图2,∵A(3,0),B(0,6), ∴E(,3),AB==3, ∵OE是Rt△OAB斜边上的中线, ∴OE=AB=,BE=, ∵EM⊥x轴, ∴F的横坐标为, ∵△OEF∽△OBE, ∴=, ∴, ∴EF=, ∴FM=3﹣=. ∴F(,), ∴k2=×=. 4.如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G. (1)当点E是BD的中点时,求tan∠AFB的值; (2)CE•AF的值是否随线段AD长度的改变而变化?如果不变,求出CE•AF的值;如果变化,请说明理由; (3)当△BGE和△BAF相似时,求线段AF的长. 【分析】(1)过点E作EH⊥CD于H,如图1,易证EH是△DBC的中位线及△AHE∽△EHD,设AH=x,运用相似三角形的性质可求出x,就可求出tan∠AFB的值; (2)取AB的中点O,连接OC、OE,如图2,易证四点A、C、B、E共圆,根据圆周角定理可得∠BCE=∠BAF,根据圆内接四边形内角互补可得∠CBE+∠CAE=180°,由此可推出∠CBE=∠BFA,从而可得△BCE∽△FAB,即可得到CE•FA=BC•AB,只需求出AB就可解决问题; (3)过点E作EH⊥CD于H,作EM⊥BC于M,如图3,易证四边形EMCH是矩形,由△BCE∽△FAB,△BGE与△FAB相似可得△BGE与△BCE相似,即可得到∠EBG=∠ECB.由点A、C、B、E共圆可得∠ECA=∠EBG,即可得到∠ECB=∠ECA,根据角平分线的性质可得EM=EH,即可得到矩形EMCH是正方形,则有CM=CH,易证EB=EA,根据HL可得Rt△BME∽Rt△AHE,则有BM=AH.设AH=x,根据CM=CH可求出x,由此可求出CE的长,再利用(2)中的结果就可求出AF的值. 【解答】解:(1)过点E作EH⊥CD于H,如图1, 则有∠EHA=∠EHD=90°. ∵∠BCD=90°,BE=DE, ∴CE=DE. ∴CH=DH, ∴EH=BC=. 设AH=x,则DH=CH=x+1. ∵AE⊥BD, ∴∠AEH+∠DEH=∠AED=90°. ∵∠AEH+∠EAH=90°, ∴∠EAH=∠DEH, ∴△AHE∽△EHD, ∴=, ∴EH2=AH•DH, ∴()2=x(x+1), 解得x=(舍负), ∴tan∠EAH===. ∵BF∥CD, ∴∠AFB=∠EAH, ∴tan∠AFB=; (2)CE•AF的值不变. 取AB的中点O,连接OC、OE,如图2, ∵∠BCA=∠BEA=90°, ∴OC=OA=OB=OE, ∴点A、C、B、E共圆, ∴∠BCE=∠BAF,∠CBE+∠CAE=180°. ∵BF∥CD, ∴∠BFA+∠CAE=180°, ∴∠CBE=∠BFA, ∴△BCE∽△FAB, ∴=, ∴CE•FA=BC•AB. ∵∠BCA=90°,BC=7,AC=1, ∴AB=5, ∴CE•FA=7×5=35; (3)过点E作EH⊥CD于H,作EM⊥BC于M,如图3, ∴∠EMC=∠MCH=∠CHE=90°, ∴四边形EMCH是矩形. ∵△BCE∽△FAB,△BGE与△FAB相似, ∴△BGE与△BCE相似, ∴∠EBG=∠ECB. ∵点A、C、B、E共圆, ∴∠ECA=∠EBG, ∴∠ECB=∠ECA, ∴EM=EH, ∴矩形EMCH是正方形, ∴CM=CH. ∵∠ECB=∠ECA=∠BCA=45°, ∴∠EBA=∠EAB=45°, ∴EB=EA, ∴Rt△BME≌Rt△AHE(HL), ∴BM=AH. 设AH=x,则BM=x,CM=7﹣x,CH=1+x, ∴7﹣x=1+x, ∴x=3, ∴CH=4. 在Rt△CHE中, cos∠ECH===, ∴CE=4. 由(2)可得CE•FA=35, ∴AF==. 5.如图,平面直角坐标系xOy中,已知B(﹣1,0),一次函数y=﹣x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=﹣x2+bx+c的图象经过点A、点B. (1)求这个二次函数的解析式; (2)点P是该二次函数图象的顶点,求△APC的面积; (3)如果点Q在线段AC上,且△ABC与△AOQ相似,求点Q的坐标. 【分析】 (1)由一次函数的解析式求出A、C两点坐标,再根据A、B两点坐标求出b、c即可确定二次函数解析式; (2)根据二次函数的解析式求出P点坐标,然后计算三角形APC的面积; (3)分两种情况讨论:①△ABC∽△AOQ,②△ABC∽△AQO. 【解答】解:(1)∵一次函数y=﹣x+5的图象与x轴、y轴分别交于点A、C两点, ∴A(5,0),C(0,5), ∵二次函数y=﹣x2+bx+c的图象经过点A、点B, ∴b=4,c=5, ∴二次函数的解析式为:y=﹣x2+4x+5. (2)∵y=﹣x2+4x+5=﹣(x﹣2)2+9, ∴P(2,9), 过点P作PD∥y轴交AC于点D,如图, 则D(2,3), ∴=15; (3)①若△ABC∽△AOQ,如图, 此时,OQ∥BC, 由B、C两点坐标可求得BC的解析式为:y=5x+5, ∴OQ的解析式为:y=5x, 由解得:, ∴Q(,); ②若△ABC∽△AQO,如图, 此时,, ∵AB=6,AO=5,AC=, ∴AQ=3, ∴Q(2,3). 综上所述,满足要求的Q点坐标为:Q(,)或Q(2,3). 6.已知:半圆O的直径AB=6,点C在半圆O上,且tan∠ABC=2,点D为弧AC上一点,联结DC(如图) (1)求BC的长; (2)若射线DC交射线AB于点M,且△MBC与△MOC相似,求CD的长; (3)联结OD,当OD∥BC时,作∠DOB的平分线交线段DC于点N,求ON的长. 【分析】(1)如图1中,根据AB是直径,得△ABC是直角三角形,利用勾股定理即可解决问题. (2)如图2中,只要证明△OBC≌△OCD得BC=CD,即可解决问题. (3)如图3中,延长ON交BC的延长线于G,作GH⊥OB于H,先求出BG,根据tan∠HBG=2,利用勾股定理求出线段HB、HG,再利用CG∥DO得,由此即可解决. 【解答】解;(1)如图1中,连接AC, ∵AB是直径, ∴∠ACB=90°, ∵tan∠ABC=2, ∴可以假设AC=2k,BC=k, ∵AB=6,AB2=AC2+BC2, ∴36=8k2+k2, ∴k2=4, ∵k>0, ∴k=2,BC=2. (2)如图2中, ∵△MBC与△MOC相似, ∴∠MBC=∠MCO, ∵∠MBC+∠OBC=180°,∠MCO+∠OCD=180°, ∴∠OBC=∠OCD, ∵OB=OC=OD, ∴∠OBC=∠OCB=∠OCD=∠ODC, 在△OBC和△OCD中, , ∴△OBC≌△OCD, ∴BC=CD=2. (3)如图3中,延长ON交BC的延长线于G,作GH⊥OB于H. ∵BC∥OD, ∴∠DOG=∠OGB=∠GOB, ∴BO=BG=3, ∵tan∠HBG=,设GH=2a,HB=a, ∵BG2=GH2+HB2, ∴8a2+a2=9, ∴a2=1, ∵a>0, ∴a=1,HB=1,GH=2,OH=2,OG==2, ∵GC∥DO, ∴=, ∴ON=×=. 7.如图,已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(3,﹣1),点C(0,﹣4),顶点为点M,过点A作AB∥x轴,交y轴与点D,交该二次函数图象于点B,连结BC. (1)求该二次函数的解析式及点M的坐标; (2)若将该二次函数图象向上平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包含△ABC的边界),求m的取值范围; (3)点P时直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程). 【分析】(1)把A、C两点的坐标代入抛物线的解析式可求b、c的值,然后利用配方法可求得点M的坐标; (2)先求得直线AC的解析式,然后再求得抛物线的对称轴,设直线x=1与△ABC的两边分别交于点E与点F,然后求得点E和点F的坐标,然后依据平移后抛物线的顶点在△BAC的内部列不等式组求解即可; (3)先证明∠PCM为直角,然后分为△MPC∽△CBD、BDC∽△MCP,两种情况求得PC的长,然后再求得点P的坐标即可. 【解答】解:(1)把A、C两点的坐标代入得:, 解得:. ∴二次函数的解析式为y=x2﹣2x﹣4. 配方得:y=(x﹣1)2﹣5. ∴点M的坐标为(1,﹣5). (2)设直线AC的解析式为y=kx+b,把点A、C的坐标代入得:,解得:, ∴直线AC的解析式为y=x﹣4. 抛物线的对称轴方程为x=﹣=1. 如图1所示,直线x=1与△ABC的两边分别交于点E与点F,则点F的坐标为(1,﹣1). 将x=1代入直线y=x﹣4得:y=﹣3. ∴E(1,﹣3). ∵抛物线向上平移m个单位长度时,抛物线的顶点在△BAC的内部, ∴﹣3<﹣5+m<﹣1. ∴2<m<4. (3)如图2所示: 把y=﹣1代入抛物线的解析式得:x2﹣2x﹣4=﹣1,解得x=﹣1或x=3, ∴B(﹣1,﹣1). ∴BD=1. ∵AB∥x轴,A(4,﹣1), ∴D(0,﹣1) ∴AD=DC=3. ∴∠DCA=45°. 过点M作ME⊥y轴,垂足为E. ∵C(0,﹣4),M(1,﹣5). ∴CE=ME=1. ∴∠ECM=45°,MC=. ∴∠ACM=90°. ∴∠PCM=∠CDB=90°. ①当△MPC∽△CBD时,,即=,解得PC=. ∴CF=PF=sin45°•PC=×=. ∴P(﹣,﹣). 如图3所示:点P在点C的右侧时,过点P作PF⊥y轴,垂足为F. ∵CP=,∠FCP=45°,∠CFP=90°, ∴CF=FP=×=. ∴P(﹣,﹣). ②当BDC∽△MCP时,=,即=,解得PC=3. 如图4所示:当点P在AC的延长线上时,过点作PE⊥y轴,垂足为E. ∵PC=3,∠PCE=45°,∠PEC=90°, ∴CE=PE=3×=3. ∴P(﹣3,﹣7). 如图5所示:当点P在AC上时,过点P作PE⊥y轴,垂足为E. ∵PC=3,∠PCE=45°,∠PEC=90°, ∴CE=PE=3×=3. ∴P(3,﹣1). 综上所述,点P的坐标为(﹣3,﹣7)或(3,﹣1)或(﹣,﹣)或(﹣,﹣). 8.如图1,在△ABC中,∠ACB=90°,∠BAC=60°,点E是∠BAC角平分线上一点,过点E作AE的垂线,过点A作AB的垂线,两垂线交于点D,连接DB,点F是BD的中点,DH⊥AC,垂足为H,连接EF,HF. (1)如图1,若点H是AC的中点,AC=2,求AB,BD的长; (2)如图1,求证:HF=EF; (3)如图2,连接CF,CE.猜想:△CEF是否是等边三角形?若是,请证明;若不是,说明理由. 【分析】(1)根据直角三角形的性质和三角函数即可得到结果; (2)如图1,连接AF,证出△DAE≌△ADH,△DHF≌△AEF,即可得到结果; (3)如图2,取AB的中点M,连接CM,FM,在Rt△ADE中,AD=2AE,根据三角形的中位线的性质得到AD=2FM,于是得到FM=AE,由∠CAE=∠CAB=30°∠ CMF=∠AMF﹣AMC=30°,证得△ACE≌△MCF,问题即可得证. 【解答】解:(1)∵∠ACB=90°,∠BAC=60°, ∴∠ABC=30°, ∴AB=2AC=2×2=4, ∵AD⊥AB,∠CAB=60°, ∴∠DAC=30°, ∵AH=AC=, ∴AD==2, ∴BD==2; (2)如图1,连接AF, ∵AE是∠BAC角平分线, ∴∠HAE=30°, ∴∠ADE=∠DAH=30°, 在△DAE与△ADH中, , ∴△DAE≌△ADH, ∴DH=AE, ∵点F是BD的中点, ∴DF=AF, ∵∠EAF=∠EAB﹣∠FAB=30°﹣∠FAB ∠FDH=∠FDA﹣∠HDA=∠FDA﹣60°=(90°﹣∠FBA)﹣60°=30°﹣∠FBA, ∴∠EAF=∠FDH, 在△DHF与△AEF中, , ∴△DHF≌△AEF, ∴HF=EF; (3)如图2,取AB的中点M,连接CM,FM, ∵F、M分别是BD、AB的中点, ∴FM∥AD,即FM⊥AB. 在Rt△ADE中,AD=2AE, ∵DF=BF,AM=BM, ∴AD=2FM, ∴FM=AE, ∵∠ABC=30°, ∴AC=CM=AB=AM, ∵∠CAE=∠CAB=30°∠CMF=∠AMF﹣∠AMC=30°, 在△ACE与△MCF中, , ∴△ACE≌△MCF, ∴CE=CF,∠ACE=∠MCF, ∵∠ACM=60°, ∴∠ECF=60°, ∴△CEF是等边三角形. 9.已知,一条抛物线的顶点为E(﹣1,4),且过点A(﹣3,0),与y轴交于点C,点D是这条抛物线上一点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴,垂足为K,DK分别交线段AE、AC于点G、H. (1)求这条抛物线的解析式; (2)求证:GH=HK; (3)当△CGH是等腰三角形时,求m的值. 【分析】(1)设抛物线的解析式为y=a(x+1)2+4 (a≠0),将点A的坐标代入求得a的值即可求得抛物线的解析式; (2)先求得直线AE、AC的解析式,由点D的横坐标为m,可求得KG、KH的长(用含m的式子),从而可证明GH=HK; (3)可分为CG=CH,GH=GC,HG=HC三种情况,接下来依据两点间的距离公式列方程求解即可. 【解答】(1)解:∵抛物线的顶点为E(﹣1,4), ∴设抛物线的解析式为y=a(x+1)2+4 (a≠0). 又∵抛物线过点A(﹣3,0), ∴4a+4=0,解得:a=﹣1. ∴这条抛物线的解析式为y=﹣(x+1)2+4. (2)设直线AE的解析式为y=kx+b. ∵将A(﹣3,0),E(﹣1,4),代入得:,解得:k=2,b=6, ∴直线AE的解析式为y=2x+6. 设直线AC的解析式为y=k1x+b1. ∵将A(﹣3,0),C(0,3)代入得:,解得:k=1,b=3, ∴直线AC的解析式为y=x+3. ∵D的横坐标为m,DK⊥x轴 ∴G(m,2m+6),H(m,m+3). ∵K(m,0) ∴GH=m+3,HK=m+3. ∴GH=HK. (3)由(2)可知:C(0,3),G(m,2m+6),H(m,m+3) ①若CG=CH,则=,整理得:(2m+3)2=m2,解得开平方得:2m+3=±m解得m1=﹣1,m2=﹣3, ∵﹣3<m<﹣1, ∴m≠﹣1且m≠﹣3. ∴这种情况不存在. ②若GC=GH,则=m+3,整理得:2m2+3m=0 解得m1=0(舍去),. ③若HC=HG,则=m+3,整理得:m2﹣6m﹣9=0,解得;m1=3﹣3,m2=3+3(舍去). 综上所述:当△CGH是等腰三角形时,m的值为或. 10.如图,已知在Rt△ABC中,∠ACB=90°,AB=5,sinA=,点P是边BC上的一点,PE⊥AB,垂足为E,以点P为圆心,PC为半径的圆与射线PE相交于点Q,线段CQ与边AB交于点D. (1)求AD的长; (2)设CP=x,△PCQ的面积为y,求y关于x的函数解析式,并写出定义域; (3)过点C作CF⊥AB,垂足为F,联结PF、QF,如果△PQF是以PF为腰的等腰三角形,求CP的长. 【分析】(1)易证AD=AC,只需运用三角函数和勾股定理求出AC即可; (2)过点Q作QH⊥BC于H,如图1,只需用x的代数式表示QH就可解决问题; (3)由于△PQF是以PF为腰的等腰三角形,故需分PF=PQ和PF=FQ两种情况讨论,只需将等腰三角形的性质和三角函数相结合,就可解决问题. 【解答】解:(1)在Rt△ABC中, ∵∠ACB=90°,AB=5,sinA=, ∴BC=AB•sinA=5×=4, ∴AC==3. ∵PC=PQ,∴∠PCQ=∠PQC. ∵PE⊥AB即∠QED=90°, ∴∠EQD+∠EDQ=90°. ∵∠ACD+∠PCQ=90°, ∴∠EDQ=∠ACD. ∵∠CDA=∠EDQ, ∴∠ACD=∠CDA, ∴AD=AC=3; (2)过点Q作QH⊥BC于H,如图1, ∵∠PBE+∠BPE=90°,∠PBE+∠A=90°, ∴∠BPE=∠A, ∴sin∠HPQ=sin∠A=, ∴sin∠HPQ==. ∵PQ=PC=x,∴QH=x, ∴S△PCQ=PC•QH=x•x=x2(≤x<4); (当E、Q、D共线时,可得x最小值,根据=,解得x=.) (3)①当PF=PQ时,则有PF=PQ=x=PC. 过点P作PG⊥CF于G,如图2, 则CG=CF. ∵CF⊥AB, ∴S△ABC=AC•BC=AB•CF, ∴CF==, ∴CG=. ∵∠PCG=90°﹣∠FCA=∠A, ∴cos∠PCG=cos∠A=, ∴cos∠PCG==, ∴x=PC=CG=×=2; ②当PF=FQ时, ∵FE⊥PQ, ∴PE=PQ=x, ∴cos∠BPE===, ∴x=. 综上所述:当△PQF是以PF为腰的等腰三角形,CP的长为2或. 11.如图(1),直线y=﹣x+n交x轴于点A,交y轴于点C(0,4),抛物线y=x2+bx+c经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m. (1)求抛物线的解析式; (2)当△BDP为等腰直角三角形时,求线段PD的长; (3)如图(2),将△BDP绕点B逆时针旋转,得到△BD′P′,当旋转角∠PBP′=∠OAC,且点P的对应点P′落在坐标轴上时,请直接写出点P的坐标. 【分析】(1)先确定出点A的坐标,再用待定系数法求出抛物线解析式; (2)由△BDP为等腰直角三角形,判断出BD=PD,建立m的方程计算出m,从而求出PD; (3)分点P′落在x轴和y轴两种情况计算即可 【解答】解:(1)∵点C(0,4)在直线y=﹣x+n上, ∴n=4, ∴y=﹣x+4, 令y=0, ∴x=3, ∴A(3,0), ∵抛物线y=x2+bx+c经过点A,交y轴于点B(0,﹣2). ∴c=﹣2,6+3b﹣2=0, ∴b=﹣, ∴抛物线解析式为y=x2﹣x﹣2, (2)∵点P的横坐标为m,且点P在抛物线上, ∴P(m,m2﹣m﹣2),D(m,﹣2). 若△BDP为等腰直角三角形,则PD=BD. ①当点P在直线BD上方时,PD=m2﹣m. (ⅰ)若点P在y轴左侧,则m<0,BD=﹣m. ∴m2﹣m=﹣m, ∴m1=0(舍去),m2=(舍去). (ⅱ)若点P在y轴右侧,则m>0,BD=m. ∴m2﹣m=m, ∴m3=0(舍去),m4=. ②当点P在直线BD下方时,m>0,BD=m,PD=﹣m2+m. ﹣m2+m=m, ∴m5=0(舍去),m6=. 综上所述,m=或m=. 即当△BDP为等腰直角三角形时,PD的长为或. (3)∵∠PBP'=∠OAC,OA=3,OC=4, ∴AC=5, ∴sin∠PBP'=,cos∠PBP'=, ①当点P'落在x轴上时,过点D'作D'N⊥x轴,垂足为N,交BD于点M, ∠DBD'=∠ND'P'=∠PBP', 如图1, 由旋转知,P'D'=PD=m2﹣m, 在Rt△P'D'N中,cos∠ND'P'==cos∠PBP'=, ∴ND'=(m2﹣m), 在Rt△BD'M中,BD'=﹣m,sin∠DBD'==sin∠PBP'=, ∴D'M=﹣m, ∴ND'﹣MD'=2, ∴(m2﹣m)﹣(﹣m)=2, ∴m=(舍),或m=﹣, 如图2, 同①的方法得,ND'=(m2﹣m),MD'=m ∵ND'+MD'=2, ∴(m2﹣m)+m=2, ∴m=,或m=﹣(舍), ∴P(﹣,)或P(,), ②当点P'落在y轴上时,如图3, 过点D′作D′M⊥x轴,交BD于M,过点P′作P′N⊥y轴,交MD'的延长线于点N, ∴∠DBD′=∠ND′P′=∠PBP′, 同①的方法得,P'N=(m2﹣m),BM=m, ∵P′N=BM, ∴(m2﹣m)=m, ∴m=, ∴P(,). ∴P(﹣,)或P(,)或P(,). 12.综合与探究 如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8). (1)求抛物线的函数表达式,并分别求出点B和点E的坐标; (2)试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由; (3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形. 【分析】(1)根据待定系数法求出抛物线解析式即可求出点B坐标,求出直线OD解析式即可解决点E坐标. (2)抛物线上存在点F使得△FOE≌△ FCE,此时点F纵坐标为﹣4,令y=﹣4即可解决问题. (3))①如图1中,当OP=OQ时,△OPQ是等腰三角形,过点E作直线ME∥PB,交y轴于点M,交x轴于点H,求出点M、H的坐标即可解决问题.②如图2中,当QO=QP时,△POQ是等腰三角形,先证明CE∥PQ,根据平行线的性质列出方程即可解决问题. 【解答】解:(1)∵抛物线y=ax2+bx﹣8经过点A(﹣2,0),D(6,﹣8), ∴,解得, ∴抛物线解析式为y=x2﹣3x﹣8, ∵y=x2﹣3x﹣8=(x﹣3)2﹣, ∴抛物线对称轴为直线x=3, 又∵抛物线与x轴交于点A、B两点,点A坐标(﹣2,0), ∴点B坐标(8,0). 设直线l的解析式为y=kx, ∵经过点D(6,﹣8), ∴6k=﹣8, ∴k=﹣, ∴直线l的解析式为y=﹣x, ∵点E为直线l与抛物线的交点, ∴点E的横坐标为3,纵坐标为﹣×3=﹣4, ∴点E坐标(3,﹣4). (2)抛物线上存在点F使得△FOE≌△FCE, 此时点F纵坐标为﹣4, ∴x2﹣3x﹣8=﹣4, ∴x2﹣6x﹣8=0, x=3, ∴点F坐标(3+,﹣4)或(3﹣,﹣4). (3)①如图1 中,当OP=OQ时,△OPQ是等腰三角形. ∵点E坐标(3,﹣4), ∴OE==5,过点E作直线ME∥PB,交y轴于点M,交x轴于点H.则=, ∴OM=OE=5, ∴点M坐标(0,﹣5). 设直线ME的解析式为y=k1x﹣5, ∴3k1﹣5=﹣4, ∴k1=, ∴直线ME解析式为y=x﹣5, 令y=0,得x﹣5=0,解得x=15, ∴点H坐标(15,0), ∵MH∥PB, ∴=,即=, ∴m=﹣, ②如图2 中,当QO=QP时,△POQ是等腰三角形. ∵当x=0时,y=x2﹣3x﹣8=﹣8, ∴点C坐标(0,﹣8), ∴CE==5, ∴OE=CE, ∴∠1=∠2, ∵QO=QP, ∴∠1=∠3, ∴∠2=∠3, ∴CE∥PB, 设直线CE交x轴于N,解析式为y=k2x﹣8, ∴3k2﹣8=﹣4, ∴k2=, ∴直线CE解析式为y=x﹣8, 令y=0,得x﹣8=0, ∴x=6, ∴点N坐标(6,0), ∵CN∥PB, ∴=, ∴=, ∴m=﹣. ③OP=PQ时,显然不可能,理由, ∵D(6,﹣8), ∴∠1<∠BOD, ∵∠OQP=∠BOQ+∠ABP, ∴∠PQO>∠1, ∴OP≠PQ, 综上所述,当m=﹣或﹣时,△OPQ是等腰三角形. 13.已知,如图1,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=11,CD=6,tan∠ABC=2,点E在AD边上,且AE=3ED,EF∥AB交BC于点F,点M、N分别在射线FE和线段CD上. (1)求线段CF的长; (2)如图2,当点M在线段FE上,且AM⊥MN,设FM•cos∠EFC=x,CN=y,求y关于x的函数解析式,并写出它的定义域; (3)如果△AMN为等腰直角三角形,求线段FM的长. 【分析】(1)过A作AH⊥BC,于是得到AH=CD=6,解直角三角形即可得到结论; (2)过M作MP⊥CD于P,MK⊥BC于K,反向延长KM交AD于Q,则KQ⊥AD,解直角三角形求得MK=2x=PC,NP=y﹣2x,MP=CK=5﹣x=QD,于是得到AQ=8﹣(5﹣x)=3+x,QM=6﹣2x,推出△AMQ∽△PMN,根据相似三角形的性质列方程即可得到结论; (3)① 当M在线段EF上时,根据全等三角形的性质和等量代换得到QM=MP,列方程得到6﹣2x=5﹣x,解方程即可得到结论;②当M在FE的延长线上时,根据已知条件得到△AQM≌△MNH,由全等三角形的性质得到AQ=MH,由(2)知FK=x,CK=5﹣x=MH,MK=2x=CH,列方程即可得到结论. 【解答】解:(1)过A作AH⊥BC, ∴AH=CD=6, ∵tan∠ABC=2, ∴, ∴BH=3, ∴CH=AD=8, ∴AE=, ∴CF=5; (2)过M作MK⊥BC于K,反向延长KM交AD于Q,则KQ⊥AD,在Rt△FMK中,FM•cos∠EFC=FK=x, ∵∠EFC=∠B, ∴tan∠EFC=2, ∴MK=2x=PC,NP=y﹣2x,MP=CK=5﹣x=QD ,∴AQ=8﹣(5﹣x)=3+x,QM=6﹣2x, ∵∠AMN=90°, ∵∠AMQ=∠PMN,∠AQM=∠MPN=90°, ∴△AMQ∽△PMN, ∴, 解得:y=(0≤x≤1); (3)①当M在线段EF上时, ∵AM=MN,△AMQ≌△NMP, ∴△AMQ≌△NMP, ∴QM=MP, ∴6﹣2x=5﹣x, ∴x=1, ∴FM=, ②当M在FE的延长线上时, ∵∠AMN=90°, ∴∠AMQ+∠NMH=∠NMH+∠MNH=90°, ∴∠AMQ=∠MNH, 在△AMQ与△NMH中,, ∴△AQM≌△MNH, ∴AQ=MH,由(2)知FK=x,CK=5﹣x=MH,MK=2x,=CH, ∴AQ=DH=2x﹣6,∴2x﹣6=5﹣x,∴, ∴FM==, 14.如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3. (1)分别求直线l1与x轴,直线l2与AB的交点坐标; (2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标; (3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由). 【分析】(1)根据坐标轴上点的坐标特征可求直线l1与x轴,直线l2与AB的交点坐标; (2)分三种情况:①若点A为直角顶点时,点M在第一象限;若点P为直角顶点时,点M在第一象限;③若点M为直角顶点时,点M在第一象限;进行讨论可求点M的坐标; (3)根据矩形的性质可求N点的横坐标x的取值范围. 【解答】解:(1)直线l1:当y=0时,2x+3=0,x=﹣ 则直线l1与x轴坐标为(﹣,0) 直线l2:当y=3时,2x﹣3=3,x=3 则直线l2与AB的交点坐标为(3,3); (2)①若点A为直角顶点时,点M在第一象限,连结AC, 如图1,∠APB>∠ACB>45°, ∴△APM不可能是等腰直角三角形, ∴点M不存在; ②若点P为直角顶点时,点M在第一象限,如图2, 过点M作MN⊥CB,交CB的延长线于点N, 则Rt△ABP≌Rt△PNM, ∴AB=PN=4,MN=BP, 设M(x,2x﹣3),则MN=x﹣4, ∴2x﹣3=4+3﹣(x﹣4), x=, ∴M(,); ③若点M为直角顶点时,点M在第一象限,如图3, 设M1(x,2x﹣3), 过点M1作M1G1⊥OA,交BC于点H1, 则Rt△AM1G1≌Rt△PM1H1, ∴AG1=M1H1=3﹣(2x﹣3), ∴x+3﹣(2x﹣3)=4, x=2 ∴M1(2,1); 设M2(x,2x﹣3), 同理可得x+2x﹣3﹣3=4, ∴x=, ∴M2(,); 综上所述,点M的坐标为(,),(2,1),(,); (3)x的取值范围为﹣≤x<0或0<x≤或≤x≤或≤x≤2. 15.如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC. (1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示); (2)点E是直线l上方的抛物线上的一点,若△ACE的面积的最大值为,求a的值; (3)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由. 【分析】(1)由抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于两点A、B,求得A点的坐标,作DF⊥x轴于F,根据平行线分线段成比例定理求得D的坐标,然后利用待定系数法法即可求得直线l的函数表达式. (2)设点E(m,a(m+1)(m﹣3)),yAE=k1x+b1,利用待定系数法确定yAE=a(m﹣3)x+a(m﹣3),从而确定S△ACE=(m+1)[a(m﹣3)﹣a]=(m﹣)2﹣a,根据最值确定a的值即可; (3)分以AD为对角线、以AC为边,AP为对角线、以AC为边,AQ为对角线三种情况利用矩形的性质确定点P的坐标即可. 【解答】解:(1)令y=0,则ax2﹣2ax﹣3a=0, 解得x1=﹣1,x2=3 ∵点A在点B的左侧, ∴A(﹣1,0), 如图1,作DF⊥x轴于F, ∴DF∥OC, ∴=, ∵CD=4AC, ∴==4, ∵OA=1, ∴OF=4, ∴D点的横坐标为4, 代入y=ax2﹣2ax﹣3a得,y=5a, ∴D(4,5a), 把A、D坐标代入y=kx+b得, 解得, ∴直线l的函数表达式为y=ax+a. (2)如图1,过点E作EN⊥y轴于点N 设点E(m,a(m+1)(m﹣3)),yAE=k1x+b1, 则, 解得:, ∴yAE=a(m﹣3)x+a(m﹣3),M(0,a(m﹣3)) ∵MC=a(m﹣3)﹣a,NE=m ∴S△ACE=S△ACM+S△CEM=[a(m﹣3)﹣a]+[a(m﹣3)﹣a]m=(m+1)[a(m﹣3)﹣a]=(m﹣)2﹣a, ∴有最大值﹣a=, ∴a=﹣; (3)令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0, 解得x1=﹣1,x2=4, ∴D(4,5a), ∵y=ax2﹣2ax﹣3a, ∴抛物线的对称轴为x=1, 设P1(1,m), ①若AD是矩形的一条边, 由AQ∥DP知xD﹣xP=xA﹣xQ,可知Q点横坐标为﹣4,将x=﹣4带入抛物线方程得Q(﹣4,21a), m=yD+yQ=21a+5a=26a,则P(1,26a), ∵四边形ADPQ为矩形,∴∠ADP=90°, ∴AD2+PD2=AP2, ∵AD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2, PD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2, ∴[4﹣(﹣1)]2+(5a)2+(1﹣4)2+(26a﹣5a)2=(﹣1﹣1)2+(26a)2, 即a2=,∵a<0,∴a=﹣, ∴P1(1,﹣). ②若AD是矩形的一条对角线, 则线段AD的中点坐标为(,),Q(2,﹣3a), m=5a﹣(﹣3a)=8a,则P(1,8a), ∵四边形ADPQ为矩形,∴∠APD=90°, ∴AP2+PD2=AD2, ∵AP2=[1﹣(﹣1)]2+(8a)2=22+(8a)2, PD2=(4﹣1)2+(8a﹣5a)2=32+(3a)2, AD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2, ∴22+(8a)2+32+(3a)2=52+(5a)2, 解得a2=,∵a<0,∴a=﹣, ∴P2(1,﹣4). 综上可得,P点的坐标为P1(1,﹣4),P2(1,﹣). 16.如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系. (1)求点E坐标及经过O,D,C三点的抛物线的解析式; (2)一动点P从点C出发,沿CB以每秒2 个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ; (3)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点的坐标;若不存在,请说明理由. 【分析】(1)由折叠的性质可求得CE、CO,在Rt△COE中,由勾股定理可求得OE即可得出点E坐标,设AD=m,在Rt△ADE中,由勾股定理可求得m的值,可求得D点坐标,结合C、O两点,利用待定系数法可求得抛物线解析式; (2)用t表示出CP、BP的长,可证明△DBP≌△DEQ,可得到BP=EQ,可求得t的值; (3)①以EN为对角线,根据对角线互相平分,可得CM的中点与EN的中点重合,根据中点坐标公式,可得m的值,根据自变量与函数值的对应关系,可得答案; ②当EM为对角线,根据对角线互相平分,可得CN的中点与EM的中点重合,根据中点坐标公式,可得m的值,根据自变量与函数值的对应关系,可得答案; ③当CE为对角线,根据对角线互相平分,可得CE的中点与MN的中点重合,根据中点坐标公式,可得m的值,根据自变量与函数值的对应关系,可得答案. 【解答】解:(1)∵CE=CB=5,CO=AB=4, ∴在Rt△COE中, OE==3. ∴E(0,﹣3) 设AD=m,则DE=BD=4﹣m, ∵OE=3, ∴AE=5﹣3=2, 在Rt△ADE中,由勾股定理可得AD2+AE2=DE2, 即m2+22=(4﹣m)2,解得m=, ∴D(﹣,﹣5), ∵C(﹣4,0),O(0,0), ∴设过O、D、C三点的抛物线为y=ax(x+4), ∴﹣5=﹣a(﹣+4),解得a=, ∴抛物线解析式为y=x(x+4)=x2+x; (2)∵CP=2t, ∴BP=5﹣2t, ∵BD=,DE==, ∴BD=DE, 在Rt△DBP和Rt△DEQ中,, ∴Rt△DBP≌Rt△DEQ(HL), ∴BP=EQ, ∴5﹣2t=t, ∴t=; (3)∵抛物线的对称为直线x=﹣2, ∴设N(﹣2,n), 又由题意可知C(﹣4,0),E(0,﹣3),设M(m,y), ①当EN为对角线,即四边形ECNM是平行四边形时,如图1, , 则线段EN的中点 横坐标为=﹣1,线段CM中点横坐标为, ∵EN,CM互相平分, ∴=﹣1,解得m=2, 又M点在抛物线上, ∴y=×22+×2=16 ∴M(2,16); ②当EM为对角线,即四边形ECMN是平行四边形时,如图2, , 则线段EM的中点, 横坐标为=m,线段CN中点横坐标为=﹣3, ∵EN,CM互相平分, ∴m=﹣3,解得m=﹣6, 又∵M点在抛物线上, ∴y=×(﹣6)2+×(﹣6)=16, ∴M(﹣6,16); ③当CE为对角线,即四边形EMCN是平行四边形时, ∴设N(﹣2,n), 又由题意可知C(﹣4,0),E(0,﹣3),设M(m,y), ∵线段CE的中点坐标的横坐标为﹣2,线段MN的中点坐标的横坐标为 ∵CE与MN互相平分,∴=﹣2 解得m=﹣2, 当m=﹣2时,y=×(﹣2)2+×(﹣2)=﹣, 即M(﹣2,﹣). 综上可知,存在满足条件的点M,其坐标为(2,16)或(﹣6,16)或(﹣2,﹣). 17.如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D和点C关于抛物线的对称轴对称,直线AD与y轴交于点E. (1)求直线AD的解析式; (2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值; (3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是以AM为边的矩形.若点T和点Q关于AM所在直线对称,求点T的坐标. 【分析】(1)先求出C(0,3),A(﹣1,0),B(3,0),再利用配方法得y=﹣(x﹣1)2+4,则抛物线对称轴为直线x=1,于是可确定D(2,3),则可利用待定系数法求直线AD的解析式; (2)由E(0,1)可判断△OAE为等腰直角三角形,则∠EAO=45°,由于FH∥OA,则可得到△FGH为等腰直角三角形,过点F作FN⊥x轴交AD于N,如图,则△FNH为等腰直角三角形,所以GH=NG,于是得到△FGH周长等于△FGN的周长,由于FG=GN=FN,则△FGN周长=(1+)FN,所以当FN最大时,△FGN周长的最大,设F(x,﹣x2+2x+3),则N(x,x+1),则FN=﹣x2+2x+3﹣x﹣1,利用二次函数的最值问题可得当x=时,FN有最大值,于是△FGN周长的最大值为; (3)直线AM交y轴于R,M(1,4),利用待定系数法求出直线AM的解析式为y=2x+2,则R(0,2),然后分类讨论:当AQ为矩形AMPQ的对角线,如图1,利用Rt△AOR∽Rt△POA,可计算出OP=,则P点坐标为(0,﹣),接着利用平移可得到Q(2, ),于是由点T和点Q关于AM所在直线对称,根据线段中点坐标公式易得T点坐标为(0,);当AP为矩形APQM的对角线,反向延长QA交y轴于S,如图2,同理可得S点坐标为(0,﹣),易得R点为AM的中点,则R点为PS的中点,所以PM=SA,P(0,),加上PM=AQ,则AQ=AS,于是可判断点Q关于AM的对称点为S,即T点坐标为(0,﹣). 【解答】解:(1)当x=0时,y=﹣x2+2x+3=3,则C(0,3), 当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0), ∵y=﹣x2+2x+3=﹣(x﹣1)2+4, ∴抛物线对称轴为直线x=1, 而点D和点C关于直线x=1对称, ∴D(2,3), 设直线AD的解析式为y=kx+b, 把A(﹣1,0),D(2,3)分别代入得,解得, ∴直线AD的解析式为y=x+1; (2)当x=0时,y=x+1=1,则E(0,1), ∵OA=OE, ∴△OAE为等腰直角三角形, ∴∠EAO=45°, ∵FH∥OA, ∴△FGH为等腰直角三角形, 过点F作FN⊥x轴交AD于N,如图, ∴FN⊥FH, ∴△FNH为等腰直角三角形, 而FG⊥HN, ∴GH=NG, ∴△FGH周长等于△FGN的周长, ∵FG=GN=FN, ∴△FGN周长=(1+)FN, ∴当FN最大时,△FGN周长的最大, 设F(x,﹣x2+2x+3),则N(x,x+1), ∴FN=﹣x2+2x+3﹣x﹣1=﹣(x﹣)2+, 当x=时,FN有最大值, ∴△FGN周长的最大值为(1+)×=, 即△FGH周长的最大值为; (3)直线AM交y轴于R,y=﹣x2+2x+3=﹣(x﹣1)2+4,则M(1,4) 设直线AM的解析式为y=mx+n, 把A(﹣1,0)、M(1,4)分别代入得,解得, ∴直线AM的解析式为y=2x+2, 当x=0时,y=2x+2=2,则R(0,2), 当AQ为矩形APQM的对角线,如图1, ∵∠RAP=90°, 而AO⊥PR, ∴Rt△AOR∽Rt△POA, ∴AO:OP=OR:OA,即1:OP=2:1,解得OP=, ∴P点坐标为(0,﹣), ∵点A(﹣1,0)向上平移4个单位,向右平移2个单位得到M(1,4), ∴点P(0,﹣)向上平移4个单位,向右平移2个单位得到Q(2,), ∵点T和点Q关于AM所在直线对称, ∴T点坐标为(0,); 当AP为矩形AMPQ的对角线,反向延长QA交y轴于S,如图2, 同理可得S点坐标为(0,﹣), ∵R点为AM的中点, ∴R点为PS的中点, ∴PM=SA,P(0,), ∵PM=AQ, ∴AQ=AS, ∴点Q关于AM的对称点为S, 即T点坐标为(0,﹣). 综上所述,点T的坐标为(0,)或(0,﹣). 18.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=CD,以DE,DF为邻边作矩形DEGF.设AQ=3x. (1)用关于x的代数式表示BQ,DF. (2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长. (3)在点P的整个运动过程中, ①当AP为何值时,矩形DEGF是正方形? ②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案). 【分析】(1)由AQ:AB=3:4,AQ=3x,易得AB=4x,由勾股定理得BQ,再由中位线的性质得AH=BH=AB,求得CD,FD; (2)利用(1)的结论,易得CQ的长,作OM⊥AQ于点M(如图1),则OM∥AB,由垂径定理得QM=AM=x,由矩形性质得OD=MC,利用矩形面积,求得x,得出结论; (3)①点P在A点的右侧时(如图1),利用(1)(2)的结论和正方形的性质得2x+4=3x,得AP;点P在A点的左侧时,当点C在Q右侧,0<x<时(如图2),4﹣7x=3x,解得x,易得AP;当时(如图3),7﹣4x=3x,得AP;当点C在Q的左侧时,即x≥(如图4),同理得AP; ②连接NQ,由点O到BN的弦心距为l,得NQ=2,当点N在AB的左侧时(如图5),过点B作BM⊥EG于点M,GM=x,BM=x,易得∠GBM=45°,BM∥AQ,易得AI=AB,求得IQ,由NQ得AP;当点N在AB的右侧时(如图6),过点B作BJ⊥GE于点J,由GJ=x,BJ=4x得tan∠GBJ=,利用(1)(2)中结论得AI=16x,QI=19x, 解得x,得AP. 【解答】解:(1)在Rt△ABQ中, ∵AQ:AB=3:4,AQ=3x, ∴AB=4x, ∴BQ=5x, ∵OD⊥m,m⊥l, ∴OD∥l, ∵OB=OQ, ∴=2x, ∴CD=2x, ∴FD==3x; (2)∵AP=AQ=3x,PC=4, ∴CQ=6x+4, 作OM⊥AQ于点M(如图1), ∴OM∥AB, ∵⊙O是△ABQ的外接圆,∠BAQ=90°, ∴点O是BQ的中点, ∴QM=AM=x ∴OD=MC=, ∴OE=BQ=, ∴ED=2x+4, S矩形DEGF=DF•DE=3x(2x+4)=90, 解得:x1=﹣5(舍去),x2=3, ∴AP=3x=9; (3)①若矩形DEGF是正方形,则ED=DF, I.点P在A点的右侧时(如图1) ∴2x+4=3x,解得:x=4, ∴AP=3x=12; II.点P在A点的左侧时, 当点C在Q右侧, 0<x<时(如图2), ∵ED=4﹣7x,DF=3x, ∴4﹣7x=3x,解得:x=, ∴AP=; 当≤x<时(如图3), ∵ED=4﹣7x,DF=3x, ∴4﹣7x=3x,解得:x=(舍去), 当点C在Q的左侧时,即x≥(如图4), DE=7x﹣4,DF=3x, ∴7x﹣4=3x,解得:x=1, ∴AP=3, 综上所述:当AP为12或或3时,矩形DEGF是正方形; ②连接NQ,由点O到BN的弦心距为l,得NQ=2, 当点N在AB的左侧时(如图5), 过点B作BM⊥EG于点M, ∵GM=x,BM=x, ∴∠GBM=45°, ∴BM∥AQ, ∴AI=AB=4x, ∴IQ=x, ∴NQ==2, ∴x=2, ∴AP=6; 当点N在AB的右侧时(如图6), 过点B作BJ⊥GE于点J, ∵GJ=x,BJ=4x, ∴tan∠GBJ=, ∴AI=16x, ∴QI=19x, ∴NQ==2, ∴x=, ∴AP=, 综上所述:AP的长为6或. 19.在平面直角坐标系xOy(如图)中,经过点A(﹣1,0)的抛物线y=﹣x2+bx+3与y轴交于点C,点B与点A、点D与点C分别关于该抛物线的对称轴对称. (1)求b的值以及直线AD与x轴正方向的夹角; (2)如果点E是抛物线上一动点,过E作EF平行于x轴交直线AD于点F,且F在E的右边,过点E作EG⊥AD与点G,设E的横坐标为m,△ EFG的周长为l,试用m表示l; (3)点M是该抛物线的顶点,点P是y轴上一点,Q是坐标平面内一点,如果以点A、M、P、Q为顶点的四边形是矩形,求该矩形的顶点Q的坐标. 【分析】(1)将点A(﹣1,0)代入抛物线的解析式可求得b的值,然后可得到抛物线的解析式,从而可求得抛物线的对称轴,再依据对称性可求得D(2,3),B(3,0),最后依据待定系数法求得AD的解析式可求得直线AD与x轴正方向的夹角; (2)设E(m,﹣m2+2m+3),则F(﹣m2+2m+2,﹣m2+2m+3),EF=﹣m2+m+2.然后证明△EFG为等腰直角三角形,从而得到EF=(1+)EF,于是可求得l与m的关系式; (3)先利用配方法求得点M的坐标,然后根据①AM为矩形的对角线时,②当AM为矩形的一边时两种情况求解即可. 【解答】解:(1)∵将点A(﹣1,0)代入抛物线的解析式得:﹣1﹣b+3=0,解得:b=2, ∴y=﹣x2+2x+3. ∴抛物线的对称轴为直线x=1. 令x=0得:y=3,则C(0,3). ∵点B与点A、点D与点C分别关于该抛物线的对称轴对称, ∴D(2,3),B(3,0). 设直线AD的解析式为y=kx+b. ∵将A(﹣1,0)、D(2,3)代入得:,解得:k=1,b=1, ∴直线AD的解析式为y=x+1. ∴直线AD与x轴正方向的夹角为45°. (2)如图1所示: 设E(m,﹣m2+2m+3),则F(﹣m2+2m+2,﹣m2+2m+3),EF=﹣m2+2m+2﹣m=﹣m2+m+2. ∵∠EGF=90°,∠EFG=45°, ∴△EFG为等腰直角三角形. ∴l=EF+FG+EG=EF+EF+EF=(1+)EF=(1+)(﹣m2+m+2)=﹣()m2+(+1)m+2+2. (3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4, ∴M(1,4). ①AM为矩形的对角线时,如图2所示: ∵由矩形的性质可知:N为AM的中点,A(﹣1,0),M(1,4), ∴N(0,2). ∵由两点间的距离公式可知:MN==. ∴NQ1=NQ2=, ∴Q1(0,2+),Q2(0,2﹣). ②当AM为矩形的一边时,如图3所示:过Q3作Q3E⊥y轴,垂直为E,过Q4作Q4F⊥y轴,垂足为F. ∵在△ANO中,AO=1,ON=2, ∴tan∠ANO=, ∴tan∠MNP4=, ∴P4MMN=,NP4=MN=. ∴P4Q3=. ∴P4E=P4Q3=1,EQ3=P4Q3=2. ∵OE=OP4﹣P4E=4.5﹣1=3.5, ∴Q3的坐标为(2,3.5). ∵点Q3与Q4关于点N对称, ∴Q4(﹣2,). 综上所述,点Q的坐标为(0,2+),或(0,2﹣)或(2,3.5)或(﹣2,). 20.如图,直线y=mx+4与反比例函数y=(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2. (1)求反比例函数解析式; (2)联结BO,求∠DBO的正切值; (3)点M在直线x=﹣1上,点N在反比例函数图象上,如果以点A、B、M、N为顶点的四边形是平行四边形,求点N的坐标. 【分析】(1)先求出C点坐标,再由tan∠CDO=2可得出D点坐标,进而可得出直线y=mx+4的解析式,根据AC:CD=1:2可得出A点坐标,进而得出反比例函数的解析式; (2)过点O作OE⊥AB于点E,根据直角三角形的面积公式求出OE的长,再由△ODE∽△CDO得出DE的长,根据锐角三角函数的定义即可得出结论; (3)设M(﹣1,y),N(x,),再分AB、AN、AM为平行四边形的对角线即可得出结论. 【解答】解:(1)∵直线y=mx+4与y轴交与点C, ∴C(0,4). ∵tan∠CDO=2, ∴OD=2,即D(﹣2,0), ∴﹣2m+4=0,解得m=2,CD==2, ∴直线y=mx+4的解析式为y=2x+4. 设A(x,2x+4), ∵AC:CD=1:2, ∴AC=, ∴=,解得x=±1, ∵点A在第一象限, ∴x=1, ∴A(1,6). ∵点A在反比例函数y=的图象上, ∴k=6, ∴反比例函数的解析式为y=; (2)过点O作OE⊥AB于点E, ∵OD=2,OC=4,CD=2, ∴OE===. ∵∠ODE=∠ODE,∠OED=∠COD, ∴△ODE∽△CDO, ∴=,即DE===. ∵,解得或, ∴B(﹣3,﹣2). ∴BD==, ∴BE=BD+DE=+=, ∴tan∠DBO===. (3)设M(﹣1,y),N(x,), ∵A(1,6),B(﹣3,﹣2), ∴当AB为平行四边形的对角线时,=,解得x=﹣1, ∴N(﹣1,﹣6); 当AN为平行四边形的对角线时,x+1=﹣3﹣1,解得x=﹣5, ∴N(﹣5,﹣); 当AM为平行四边形的对角线时,0=x﹣3,解得x=3, ∴N(3,2). 综上所述,N(﹣1,﹣6)或(﹣5,﹣)或(3,2). 21.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B. (1)求二次函数y=ax2+bx+c的表达式; (2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积; (3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标. 【分析】(1)设出抛物线解析式,用待定系数法求解即可; (2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立函数关系式S四边形APCD=﹣2x2+10x,根据二次函数求出极值; (3)方法1、先判断出△HMN≌△AOE,求出M点的横坐标,从而求出点M,N的坐标. 方法2、四边形AENM是平行四边形时,由于知道点E和点N的横坐标,进而得出点E平移到点N时,先向右平移3单位,进而判断出点A到点M向右先平移3个单位,求出点M的横坐标,代入抛物线解析式,即可求出点M坐标,判断出点A再向上平移3个单位得出点M,即可求出点N坐标;四边形AEMN是平行四边形时,同上方法即可得出结论. 【解答】解:(1)设抛物线解析式为y=a(x﹣2)2+9, ∵抛物线与y轴交于点A(0,5), ∴4a+9=5, ∴a=﹣1, y=﹣(x﹣2)2+9=﹣x2+4x+5, (2)当y=0时,﹣x2+4x+5=0, ∴x1=﹣1,x2=5, ∴E(﹣1,0),B(5,0), 设直线AB的解析式为y=mx+n, ∵A(0,5),B(5,0), ∴m=﹣1,n=5, ∴直线AB的解析式为y=﹣x+5; 设P(x,﹣x2+4x+5), ∴D(x,﹣x+5), ∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x, ∵AC=4, ∴S四边形APCD=×AC×PD=2(﹣x2+5x)=﹣2x2+10x, ∴当x=﹣=时, ∴即:点P(,)时,S四边形APCD最大=, (3)方法1、如图, 过M作MH垂直于对称轴,垂足为H, ∵MN∥AE,MN=AE, ∴△HMN≌△AOE, ∴HM=OE=1, ∴M点的横坐标为x=3或x=1, 当x=1时,M点纵坐标为8, 当x=3时,M点纵坐标为8, ∴M点的坐标为M1(1,8)或M2(3,8), ∵A(0,5),E(﹣1,0), ∴直线AE解析式为y=5x+5, ∵MN∥AE, ∴MN的解析式为y=5x+b, ∵点N在抛物线对称轴x=2上, ∴N(2,10+b), ∵AE2=OA2+OE2=26 ∵MN=AE ∴MN2=AE2, ∴MN2=(2﹣1)2+[8﹣(10+b)]2=1+(b+2)2 ∵M点的坐标为M1(1,8)或M2(3,8), ∴点M1,M2关于抛物线对称轴x=2对称, ∵点N在抛物线对称轴上, ∴M1N=M2N, ∴1+(b+2)2=26, ∴b=3,或b=﹣7, ∴10+b=13或10+b=3 ∴当M点的坐标为(1,8)时,N点坐标为(2,13), 当M点的坐标为(3,8)时,N点坐标为(2,3). 方法2,如图1, ∴E(﹣1,0),A(0,5), ∵抛物线的解析式为y=﹣(x﹣2)2+9, ∴抛物线的对称轴为直线x=2, ∴点N的横坐标为2,即:N'(2,0) ①当以点A,E,M,N组成的平行四边形为四边形AENM时, ∵E(﹣1,0),点N的横坐标为2,(N'(2,0) ∴点E到点N向右平移2﹣(﹣1)=3个单位, ∵四边形AENM是平行四边形, ∴点A向右也平移3个单位, ∵A(0,5), ∴M点的横坐标为3,即:M'(3,5), ∵点M在抛物线上, ∴点M的纵坐标为﹣(3﹣2)2+9=8, ∴M(3,8),即:点A再向上平移(8﹣5=3)个单位, ∴点N'再向上平移3个单位,得到点N(2,3), 即:当M点的坐标为(3,8)时,N点坐标为(2,3). ②当以点A,E,M,N组成的平行四边形为四边形AEMN时, 同①的方法得出,当M点的坐标为(1,8)时,N点坐标为(2,13). 22.如图,在平面直角坐标系xOy中,二次函数y=+bx+c的图象与y轴交于点A,与双曲线y=有一个公共点B,它的横坐标为4,过点B作直线l∥x轴,与该二次函数图象交于另一个点C,直线AC在y轴上的截距是﹣6. (1)求二次函数的解析式; (2)求直线AC的表达式; (3)平面内是否存在点D,使A、B、C、D为顶点的四边形是等腰梯形?如果存在,求出点D坐标;如果不存在,说明理由. 【分析】(1)先求得点A与点B的坐标,然后依据待定系数法可求得抛物线的解析式; (2)先求得抛物线的对称轴为x=﹣1,依据点B与点C关于x=﹣1对称,可求得点C的坐标,然后依据待定系数法可求得直线AC的解析式; (3)①当CD∥AB时,AC=BC,故点D不存在;②如图1所示:当AD∥ BC时,AB<AC,过点A作BC平行线l,以C为圆心,AB为半径作弧,交l与点D1点,依据点A与D1关于x=﹣1对称可求得点D1的坐标;③如图2所示:BD∥AC时,过点C作CM⊥x轴,过点A作AM⊥y轴,过点B作BF⊥AC,D2E⊥AC.先依据AAS证明△AMC≌△CBF,从而可求得AF=CE=4,于是得到D2B=2,然后再证明BHD2∽△AMC,从而可求得BH=,HD2=,于是可求得点D2的坐标. 【解答】解:(1)∵将x=4代入y=得:y=2, ∴B(4,2). ∵点A在y轴上,且直线AC在y轴上的截距是﹣6, ∴A(0,﹣6). ∵将B(4,2)、A(0,﹣6)代入抛物线的解析式得:,解得:, ∴抛物线的解析式为y=+﹣6. (2)∵抛物线的对称轴为x=﹣=﹣1. ∴点B关于x=﹣1的对称点C的坐标为(﹣6,2). 设直线AC的解析式为y=kx+b. ∵将点A(0,﹣6)、C(﹣6,2)代入得:,解得:k=﹣,b=﹣6, ∴直线AC的解析式为y=﹣6. (3)①∵B(4,2)C(﹣6,2), ∴BC=10. ∵A(0,﹣6)、C(﹣6,2), ∴AC==10. ∴AC=BC. ∴当CD∥AB时,不存在点D使得四边形A、B、C、D为顶点的四边形是等腰梯形. ②如图1所示: 当AD∥BC时,AB<AC,过点A作BC平行线l,以C为圆心,AB为半径作弧,交l与点D1点,A与D1关于x=﹣1对称, ∴D1(﹣2,﹣6). ③如图2所示:BD∥AC时,过点C作CM⊥x轴,过点A作AM⊥y轴,过点B作BF⊥AC,D2E⊥AC. ∵CB∥AM, ∴∠BCA=∠CAM. 在△AMC和△CBF中, , ∴△AMC≌△CBF. ∴CF=AM=6. ∴AF=4. ∵梯形ABD2C是等腰梯形, ∴CE=AF=4. ∴D2B=EF=2. ∵BD2∥AC, ∴∠D2BH=∠BCA. ∵∠BCA=∠CAM, ∴∠D2BH=∠CAM. 又∵∠M=∠D2HB, ∴BHD2∽△AMC. ∴. ∵BD2=2, ∴BH=,HD2=, ∴D2(,). 综上所述,点D的坐标为(﹣2,﹣6)或D2(,). 23.如图,矩形OMPN的顶点O在原点,M、N分别在x轴和y轴的正半轴上,OM=6,ON=3,反比例函数y=的图象与PN交于C,与PM交于D,过点C作CA⊥x轴于点A,过点D作DB⊥y轴于点B,AC与BD交于点G. (1)求证:AB∥CD; (2)在直角坐标平面内是否若存在点E,使以B、C、D、E为顶点,BC为腰的梯形是等腰梯形?若存在,求点E的坐标;若不存在请说明理由. 【分析】(1)首先求得C和D的坐标,证明=即可证得; (2)分成PN∥DB和CD∥AB两种情况进行讨论,即可求解. 【解答】(1)证明:∵四边形OMPN是矩形,OM=6,ON=3, ∴P的坐标是(6,3). ∵点C和D都在反比例函数y=的图象上,且点C在PN上,点D在PM上, ∴点C(2,3),点D(6,1). 又∵DB⊥y轴,CA⊥x轴, ∴A的坐标是(2,0),B的坐标是(0,1). ∵BG=2,GD=4,CG=2,AG=1. ∴=,==, ∴=, ∴AB∥CD; (2)解:①∵PN∥DB, ∴当DE1=BC时,四边形BCE1D是等腰梯形,此时直角△CNB≌直角△E1PD, ∴PE1=CN=2, ∴点E1的坐标是(4,3); ②∵CD∥AB,当E2在直线AB上,DE2=BC=2,四边形BCDE2为等腰梯形, 直线AB的解析式是y=﹣x+1, ∴设点E2(x,﹣x+1),DE2=BC=2, ∴(x﹣6)2+(x)2=8, 解得:x1=,x2=4(舍去). ∴E2的坐标是(,﹣). 24.如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含端点),过点P作PF⊥BC于点F,点D、E的坐标分别为(0,6),(﹣4,0),连接PD、PE、DE. (1)请直接写出抛物线的解析式; (2)小明探究点P的位置发现:当P与点A或点C重合时,PD与PF的差为定值,进而猜想:对于任意一点P,PD与PF的差为定值,请你判断该猜想是否正确,并说明理由; (3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE周长最小时“好点”的坐标. 【分析】(1)利用待定系数法求出抛物线解析式即可; (2)首先表示出P,F点坐标,再利用两点之间距离公式得出PD,PF的长,进而求出即可; (3)根据题意当P、E、F三点共线时,PE+PF最小,进而得出P点坐标以及利用△PDE的面积可以等于4到13所有整数,在面积为12时,a的值有两个,进而得出答案. 【解答】解:(1)∵边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A, ∴C(0,8),A(﹣8,0), 设抛物线解析式为:y=ax2+c, 则, 解得: 故抛物线的解析式为:y=﹣x2+8; (2)正确, 理由:设P(a,﹣a2+8),则F(a,8), ∵D(0,6), ∴PD===a2+2, PF=8﹣(﹣a2+8)=a2, ∴PD﹣PF=2; (3)在点P运动时,DE大小不变,则PE与PD的和最小时,△PDE的周长最小, ∵PD﹣PF=2,∴PD=PF+2, ∴PE+PD=PE+PF+2, ∴当P、E、F三点共线时,PE+PF最小, 此时点P,E的横坐标都为﹣4, 将x=﹣4代入y=﹣x2+8,得y=6, ∴P(﹣4,6),此时△PDE的周长最小,且△PDE的面积为12,点P恰为“好点, ∴△PDE的周长最小时”好点“的坐标为:(﹣4,6), 由(2)得:P(a,﹣a2+8), ∵点D、E的坐标分别为(0,6),(﹣4,0), ①当﹣4≤a<0时,S△PDE=(﹣a+4)(﹣a2+8)﹣[﹣•(﹣a2+8﹣6)=; ∴4<S△PDE≤12, ②当a=0时,S△PDE=4, ③﹣8<a<﹣4时,S△PDE=(﹣a2+8+6)×(﹣a)×﹣×4×6﹣(﹣a﹣4)×(﹣a2+8)× =﹣a2﹣3a+4, ∴12≤S△PDE≤13, ④当a=﹣8时,S△PDE=12, ∴△PDE的面积可以等于4到13所有整数,在面积为12时,a的值有两个, 所以面积为整数时好点有11个,经过验证周长最小的好点包含这11个之内,所以好点共11个, 综上所述:11个好点,P(﹣4,6). 25.如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t. (1)求点M的坐标(用含t的代数式表示). (2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由. (3)当t为何值时,四边形BNDM的面积最小. 【分析】(1)作ME⊥x轴于E,则∠MEP=90°,先证出∠PME=∠CPO,再证明△MPE≌△PCO,得出ME=PO=t,EP=OC=4,求出OE,即可得出点M的坐标; (2)连接AM,先证明四边形AEMF是正方形,得出∠MAE=45°=∠BOA,AM∥OB,证出四边形OAMN是平行四边形,即可得出MN=OA=4; (3)先证明△PAD∽△PEM,得出比例式,得出AD,求出BD,求出四边形BNDM的面积S是关于t的二次函数,即可得出结果. 【解答】解:(1)作ME⊥x轴于E,如图1所示: 则∠MEP=90°,ME∥AB, ∴∠MPE+∠PME=90°, ∵四边形OABC是正方形, ∴∠POC=90°,OA=OC=AB=BC=4,∠BOA=45°, ∵PM⊥CP, ∴∠CPM=90°, ∴∠MPE+∠CPO=90°, ∴∠PME=∠CPO, 在△MPE和△PCO中,, ∴△MPE≌△PCO(AAS), ∴ME=PO=t,EP=OC=4, ∴OE=t+4, ∴点M的坐标为:(t+4,t); (2)线段MN的长度不发生改变;理由如下: 连接AM,如图2所示: ∵MN∥OA,ME∥AB,∠MEA=90°, ∴四边形AEMF是矩形, 又∵EP=OC=OA, ∴AE=PO=t=ME, ∴四边形AEMF是正方形, ∴∠MAE=45°=∠BOA, ∴AM∥OB, ∴四边形OAMN是平行四边形, ∴MN=OA=4; (3)∵ME∥AB, ∴△PAD∽△PEM, ∴, 即, ∴AD=﹣t2+t, ∴BD=AB﹣AD=4﹣(﹣t2+t)=t2﹣t+4, ∵MN∥OA,AB⊥OA, ∴MN⊥AB, ∴四边形BNDM的面积S=MN•BD=×4(t2﹣t+4)=(t﹣2)2+6, ∴S是t的二次函数, ∵>0, ∴S有最小值, 当t=2时,S的值最小; ∴当t=2时,四边形BNDM的面积最小. 26.在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上. (1)小明发现DG⊥BE,请你帮他说明理由. (2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长. (3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由. 【分析】(1)由四边形ABCD与四边形AEFG为正方形,利用正方形的性质得到两对边相等,且夹角相等,利用SAS得到三角形ADG与三角形ABE全等,利用全等三角形对应角相等得∠AGD=∠AEB,如图1所示,延长EB交DG于点H,利用等角的余角相等得到∠DHE=90°,利用垂直的定义即可得DG⊥BE; (2)由四边形ABCD与四边形AEFG为正方形,利用正方形的性质得到两对边相等,且夹角相等,利用SAS得到三角形ADG与三角形ABE全等,利用全等三角形对应边相等得到DG=BE,如图2,过点A作AM⊥DG交DG于点M,∠AMD=∠AMG=90°,在直角三角形AMD中,求出AM的长,即为DM的长,根据勾股定理求出GM的长,进而确定出DG的长,即为BE的长; (3)△GHE和△BHD面积之和的最大值为6,理由为:对于△EGH,点H在以EG为直径的圆上,即当点H与点A重合时,△EGH的高最大;对于△BDH,点H在以BD为直径的圆上,即当点H与点A重合时,△BDH的高最大,即可确定出面积的最大值. 【解答】解:(1)∵四边形ABCD和四边形AEFG都为正方形, ∴AD=AB,∠DAG=∠BAE=90°,AG=AE, 在△ADG和△ABE中, , ∴△ADG≌△ABE(SAS), ∴∠AGD=∠AEB, 如图1所示,延长EB交DG于点H, 在△ADG中,∠AGD+∠ADG=90°, ∴∠AEB+∠ADG=90°, 在△EDH中,∠AEB+∠ADG+∠DHE=180°, ∴∠DHE=90°, 则DG⊥BE; (2)∵四边形ABCD和四边形AEFG都为正方形, ∴AD=AB,∠DAB=∠GAE=90°,AG=AE, ∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE, 在△ADG和△ABE中, ∴△ADG≌△ABE(SAS), ∴DG=BE, 如图2,过点A作AM⊥DG交DG于点M,∠AMD=∠AMG=90°, ∵BD为正方形ABCD的对角线, ∴∠MDA=45°, 在Rt△AMD中,∠MDA=45°, ∴cos45°=, ∵AD=2, ∴DM=AM=, 在Rt△AMG中,根据勾股定理得:GM==, ∵DG=DM+GM=+, ∴BE=DG=+; (3)△GHE和△BHD面积之和的最大值为6,理由为: 对于△EGH,点H在以EG为直径的圆上, ∴当点H与点A重合时,△EGH的高最大; 对于△BDH,点H在以BD为直径的圆上, ∴当点H与点A重合时,△BDH的高最大, 则△GHE和△BHD面积之和的最大值为2+4=6. 27.在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C. (1)求过A,B,C三点的抛物线的解析式; (2)P为抛物线上一点,它关于原点的对称点为Q. ①当四边形PBQC为菱形时,求点P的坐标; ②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大?并说明理由. 【分析】(1)联立两直线解析式可求得B点坐标,由关于原点对称可求得C点坐标,由直线y=﹣2x﹣1可求得A点坐标,再利用待定系数法可求得抛物线解析式; (2)①当四边形PBQC为菱形时,可知PQ⊥BC,则可求得直线PQ的解析式,联立抛物线解析式可求得P点坐标;②过P作PD⊥BC,垂足为D,作x轴的垂线,交直线BC于点E,由∠PED=∠AOC,可知当PE最大时,PD也最大,用t可表示出PE的长,可求得取最大值时的t的值. 【解答】解: (1)联立两直线解析式可得,解得, ∴B点坐标为(﹣1,1), 又C点为B点关于原点的对称点, ∴C点坐标为(1,﹣1), ∵直线y=﹣2x﹣1与y轴交于点A, ∴A点坐标为(0,﹣1), 设抛物线解析式为y=ax2+bx+c, 把A、B、C三点坐标代入可得,解得, ∴抛物线解析式为y=x2﹣x﹣1; (2)①当四边形PBQC为菱形时,则PQ⊥BC, ∵直线BC解析式为y=﹣x, ∴直线PQ解析式为y=x, 联立抛物线解析式可得,解得或, ∴P点坐标为(1﹣,1﹣)或(1+,1+); ②当t=0时,四边形PBQC的面积最大. 理由如下: 如图,过P作PD⊥BC,垂足为D,作x轴的垂线,交直线BC于点E, 则S四边形PBQC=2S△PBC=2×BC•PD=BC•PD, ∵线段BC长固定不变, ∴当PD最大时,四边形PBQC面积最大, 又∠PED=∠AOC(固定不变), ∴当PE最大时,PD也最大, ∵P点在抛物线上,E点在直线BC上, ∴P点坐标为(t,t2﹣t﹣1),E点坐标为(t,﹣t), ∴PE=﹣t﹣(t2﹣t﹣1)=﹣t2+1, ∴当t=0时,PE有最大值1,此时PD有最大值,即四边形PBQC的面积最大. 28.如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点. (1)∠OBA= 90 °. (2)求抛物线的函数表达式. (3)若P为抛物线上位于第一象限内的一个动点,以P、O、A、E为顶点的四边形面积记作S,则S取何值时,相应的点P有且只有3个? 【分析】(1)利用圆周角定理,直径所对的圆周角等于90°,即可得出答案; (2)利用(1)中的结论易得OB是的垂直平分线,易得点B,点C的坐标,由点O,点B的坐标易得OB所在直线的解析式,从而得出点E的坐标,用待定系数法得抛物线的解析式; (3)利用(2)的结论易得点P的坐标,分类讨论①若点P在CD的左侧,延长OP交CD于Q,如右图2,易得OP所在直线的函数关系式,表示出Q点的纵坐标, 得QE的长,表示出四边形POAE的面积;②若点P在CD的右侧,延长AP交CD于Q,如右图3,易得AP所在直线的解析式,从而求得Q点的纵坐标,得QE求得四边形POAE的面积,当P在CD右侧时,四边形POAE的面积最大值为16,此时点P的位置就一个,令=16,解得p,得出结论. 【解答】解:(1)∵OA是⊙O的直径, ∴∠OBA=90°, 故答案为:90; (2)连接OC,如图1所示, ∵由(1)知OB⊥AC,又AB=BC, ∴OB是AC的垂直平分线, ∴OC=OA=10, 在Rt△OCD中,OC=10,CD=8, ∴OD=6, ∴C(6,8),B(8,4) ∴OB所在直线的函数关系为y=x, 又∵E点的横坐标为6, ∴E点纵坐标为3, 即E(6,3), 抛物线过O(0,0),E(6,3),A(10,0), ∴设此抛物线的函数关系式为y=ax(x﹣10),把E点坐标代入得: 3=6a(6﹣10), 解得a=﹣. ∴此抛物线的函数关系式为y=﹣x(x﹣10),即y=﹣x2+x; (3)设点P(p,﹣p2+p), ①若点P在CD的左侧,延长OP交CD于Q,如右图2, OP所在直线函数关系式为:y=(﹣p+)x ∴当x=6时,y=,即Q点纵坐标为, ∴QE=﹣3=, S四边形POAE =S△OAE+S△OPE =S△OAE+S△OQE﹣S△PQE =•OA•DE+QE•OD﹣•QE•Px• =×10×3+×(﹣p+)×6﹣•()•(6﹣p), = ②若点P在CD的右侧,延长AP交CD于Q,如右图3, P(p,﹣p2+p),A(10,0) ∴设AP所在直线方程为:y=kx+b,把P和A坐标代入得, , 解得. ∴AP所在直线方程为:y=x+, ∴当x=6时,y=•6+=P,即Q点纵坐标为P, ∴QE=P﹣3, ∴S四边形POAE =S△OAE+S△APE =S△OAE+S△AQE﹣S△PQE =•OA•DE+•QE•DA﹣•QE•(Px﹣6) =×10×3+•QE•(DA﹣Px+6) =15+•(p﹣3)•(10﹣p) = =, ∴当P在CD右侧时,四边形POAE的面积最大值为16,此时点P的位置就一个, 令=16,解得,p=3±, ∴当P在CD左侧时,四边形POAE的面积等于16的对应P的位置有两个, 综上所知,以P、O、A、E为顶点的四边形面积S等于16时,相应的点P有且只有3个. 29.如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上. (1)求抛物线的解析式; (2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由; (3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由. 【分析】(1)把A、C两点坐标代入可求得b、c,可求得抛物线解析式; (2)当点P在∠DAB的平分线上时,过P作PM⊥AD,设出P点坐标,可表示出PM、PE,由角平分线的性质可得到PM=PE,可求得P点坐标;当点P在∠DAB外角平分线上时,同理可求得P点坐标; (3)可先求得△FBC的面积,过F作FQ⊥x轴,交BC的延长线于Q,可求得FQ的长,可设出F点坐标,表示出B点坐标,从而可表示出FQ的长,可求得F点坐标. 【解答】解: (1)∵二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3), ∴,解得, ∴抛物线的解析式y=﹣x2﹣2x+3, (2)存在, 当P在∠DAB的平分线上时,如图1,作PM⊥AD, 设P(﹣1,m),则PM=PD•sin∠ADE=(4﹣m),PE=m, ∵PM=PE, ∴(4﹣m)=m,m=﹣1, ∴P点坐标为(﹣1,﹣1); 当P在∠DAB的外角平分线上时,如图2,作PN⊥AD, 设P(﹣1,n),则PN=PD•sin∠ADE=(4﹣n),PE=﹣n, ∵PN=PE, ∴(4﹣n)=﹣n,n=﹣﹣1, ∴P点坐标为(﹣1,﹣﹣1); 综上可知存在满足条件的P点,其坐标为(﹣1,﹣1)或(﹣1,﹣﹣1); (3)∵抛物线的解析式y=﹣x2﹣2x+3, ∴B(1,0), ∴S△EBC=EB•OC=3, ∵2S△FBC=3S△EBC, ∴S△FBC=, 过F作FQ⊥x轴于点H,交BC的延长线于Q,过F作FM⊥y轴于点M,如图3, ∵S△FBC=S△BQH﹣S△BFH﹣S△CFQ=HB•HQ﹣BH•HF﹣QF•FM=BH(HQ﹣HF)﹣QF•FM=BH•QF﹣QF•FM=QF•(BH﹣FM)=FQ•OB=FQ=, ∴FQ=9, ∵BC的解析式为y=﹣3x+3, 设F(x0,﹣x02﹣2x0+3), ∴﹣3x0+3+x02+2x0﹣3=9, 解得:x0=或(舍去), ∴点F的坐标是(,), ∵S△ABC=6>, ∴点F不可能在A点下方, 综上可知F点的坐标为(,). 30.已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B (1)求m的取值范围; (2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标; (3)当<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值. 【分析】(1)根据题意得出△=(1﹣2m)2﹣4×m×(1﹣3m)=(1﹣4m)2>0,得出1﹣4m≠0,解不等式即可; (2)y=m(x2﹣2x﹣3)+x+1,故只要x2﹣2x﹣3=0,那么y的值便与m无关,解得x=3或x=﹣1(舍去,此时y=0,在坐标轴上),故定点为(3,4); (3)由|AB|=|xA﹣xB|得出|AB|=|﹣4|,由已知条件得出≤<4,得出0<|﹣4|≤,因此|AB|最大时,||=,解方程得出m=8,或m=(舍去),即可得出结果. 【解答】(1)解:当m=0时,函数为一次函数,不符合题意,舍去; 当m≠0时, ∵抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B, ∴△=(1﹣2m)2﹣4×m×(1﹣3m)=(1﹣4m)2>0, ∴1﹣4m≠0, ∴m≠, ∴m的取值范围为m≠0且m≠; (2)证明:∵抛物线y=mx2+(1﹣2m)x+1﹣3m, ∴y=m(x2﹣2x﹣3)+x+1, 抛物线过定点说明在这一点y与m无关, 显然当x2﹣2x﹣3=0时,y与m无关, 解得:x=3或x=﹣1, 当x=3时,y=4,定点坐标为(3,4); 当x=﹣1时,y=0,定点坐标为(﹣1,0), ∵P不在坐标轴上, ∴P(3,4); (3)解:|AB|=|xA﹣xB|=====||=|﹣4|, ∵<m≤8, ∴≤<4, ∴﹣≤﹣4<0, ∴0<|﹣4|≤, ∴|AB|最大时,||=, 解得:m=8,或m=(舍去), ∴当m=8时,|AB|有最大值, 此时△ABP的面积最大,没有最小值, 则面积最大为:|AB|yP=××4=. 31.问题提出 (1)如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形. 问题探究 (2)如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由. 问题解决 (3)如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG= 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF< BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由. 【分析】(1)作B关于AC 的对称点D,连接AD,CD,△ACD即为所求; (2)作E关于CD的对称点E′,作F关于BC的对称点F′,连接E′F′,得到此时四边形EFGH的周长最小,根据轴对称的性质得到BF′=BF=AF=2,DE′=DE=2,∠A=90°,于是得到AF′=6,AE′=8,求出E′F′=10,EF=2即可得到结论; (3)根据余角的性质得到1=∠2,推出△AEF≌△BGF,根据全等三角形的性质得到AF=BG,AE=BF,设AF=x,则AE=BF=3﹣x根据勾股定理列方程得到AF=BG=1,BF=AE=2,作△EFG关于EG的对称△EOG,则四边形EFGO是正方形,∠EOG=90°,以O为圆心,以EG为半径作⊙O,则∠EHG=45°的点H在⊙O上,连接FO,并延长交⊙O于H′,则H′在EG的垂直平分线上,连接EH′GH′,则∠EH′G=45°,于是得到四边形EFGH′是符合条件的最大部件,根据矩形的面积公式即可得到结论. 【解答】解:(1)如图1,△ADC即为所求; (2)存在,理由:作E关于CD的对称点E′, 作F关于BC的对称点F′, 连接E′F′,交BC于G,交CD于H,连接FG,EH, 则F′G=FG,E′H=EH,则此时四边形EFGH的周长最小, 由题意得:BF′=BF=AF=2,DE′=DE=2,∠A=90°, ∴AF′=6,AE′=8, ∴E′F′=10,EF=2, ∴四边形EFGH的周长的最小值=EF+FG+GH+HE=EF+E′F′=2+10, ∴在边BC、CD上分别存在点G、H, 使得四边形EFGH的周长最小, 最小值为2+10; (3)能裁得, 理由:∵EF=FG=,∠A=∠B=90°,∠1+∠AFE=∠2+AFE=90°, ∴∠1=∠2, 在△AEF与△BGF中,, ∴△AEF≌△BGF, ∴AF=BG,AE=BF,设AF=x,则AE=BF=3﹣x, ∴x2+(3﹣x)2=()2,解得:x=1,x=2(不合题意,舍去), ∴AF=BG=1,BF=AE=2, ∴DE=4,CG=5, 连接EG, 作△EFG关于EG的对称△EOG, 则四边形EFGO是正方形,∠EOG=90°, 以O为圆心,以OE为半径作⊙O, ∵CE=CG=5, 则∠EHG=45°的点在⊙O上, 连接FO,并延长交⊙O于H′,则H′在EG的垂直平分线上, 连接EH′、GH′,则∠EH′G=45°, 此时,四边形EFGH′是要想裁得符合要求的面积最大的, ∴C在线段EG的垂直平分线上, ∴点F,O,H′,C在一条直线上, ∵EG=, ∴OF=EG=, ∵CF=2, ∴OC=, ∵OH′=OE=FG=, ∴OH′<OC, ∴点H′在矩形ABCD的内部, ∴可以在矩形ABCD中,裁得符合条件的面积最大的四边形EFGH′部件, 这个部件的面积=EG•FH′=××(+)=5+, ∴当所裁得的四边形部件为四边形EFGH′时,裁得了符合条件的最大部件,这个部件的面积为(5+)m2. 32.如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y=x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K. (1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处. ①点B的坐标为( 10 、 0 ),BK的长是 8 ,CK的长是 10 ; ②求点F的坐标; ③请直接写出抛物线的函数表达式; (2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△ NOG的面积分别表示为S1和S2,在点M的运动过程中,S1•S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值. 温馨提示:考生可以根据题意,在备用图中补充图形,以便作答. 【分析】(1)①根据四边形OCKB是矩形以及对称轴公式即可解决问题. ②在RT△BKF中利用勾股定理即可解决问题. ③设OA=AF=x,在RT△ACF中,AC=8﹣x,AF=x,CF=4,利用勾股定理即可解决问题. (2)不变.S1•S2=289.由△GHN∽△MHG,得=,得到GH2=HN•HM,求出GH2,根据S1•S2=•OG•HN••OG•HM即可解决问题. 【解答】解:(1)如图1中,①∵抛物线y=x2﹣3x+m的对称轴x=﹣=10, ∴点B坐标(10,0), ∵四边形OBKC是矩形, ∴CK=OB=10,KB=OC=8, 故答案分别为10,0,8,10. ②在RT△FBK中,∵∠FKB=90°,BF=OB=10,BK=OC=8, ∴FK==6, ∴CF=CK﹣FK=4, ∴点F坐标(4,8). ③设OA=AF=x, 在RT△ACF中,∵AC2+CF2=AF2, ∴(8﹣x)2+42=x2, ∴x=5, ∴点A坐标(0,5),代入抛物线y=x2﹣3x+m得m=5, ∴抛物线为y=x2﹣3x+5. (2)不变.S1•S2=289. 理由:如图2中,在RT△EDG中,∵GE=EO=17,ED=8, ∴DG===15, ∴CG=CD﹣DG=2, ∴OG===2, ∵GP⊥OM,MH⊥OG, ∴∠NPM=∠NHG=90°, ∵∠HNG+∠HGN=90°,∠PNM+∠PMN=90°,∠HNG=∠PNM, ∴∠HGN=∠NMP, ∵∠NMP=∠HMG,∠GHN=∠GHM, ∴△GHN∽△MHG, ∴=, ∴GH2=HN•HM, ∵GH=OH=, ∴HN•HM=17, ∵S1•S2=•OG•HN••OG•HM=(•2)2•17=289. 33.如图,已知▱ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作▱ABCD关于直线AD的对称图形AB1C1D (1)若m=3,试求四边形CC1B1B面积S的最大值; (2)若点B1恰好落在y轴上,试求的值. 【分析】(1)如图1,易证S▱BCEF=S▱BCDA=S▱B1C1DA=S▱B1C1EF,从而可得S▱BCC1B1=2S▱BCDA=﹣4(n﹣)2+9,根据二次函数的最值性就可解决问题; (2)如图2,易证△AOD∽△B1OB,根据相似三角形的性质可得OB1=,然后在Rt△AOB1中运用勾股定理就可解决问题. 【解答】解:(1)如图1, ∵▱ABCD与四边形AB1C1D关于直线AD对称, ∴四边形AB1C1D是平行四边形,CC1⊥EF,BB1⊥EF, ∴BC∥AD∥B1C1,CC1∥BB1, ∴四边形BCEF、B1C1EF是平行四边形, ∴S▱BCEF=S▱BCDA=S▱B1C1DA=S▱B1C1EF, ∴S▱BCC1B1=2S▱BCDA. ∵A(n,0)、B(m,0)、D(0,2n)、m=3, ∴AB=m﹣n=3﹣n,OD=2n, ∴S▱BCDA=AB•OD=(3﹣n)•2n=﹣2(n2﹣3n)=﹣2(n﹣)2+, ∴S▱BCC1B1=2S▱BCDA=﹣4(n﹣)2+9. ∵﹣4<0,∴当n=时,S▱BCC1B1最大值为9; (2)当点B1恰好落在y轴上,如图2, ∵DF⊥BB1,DB1⊥OB, ∴∠B1DF+∠DB1F=90°,∠B1BO+∠OB1B=90°, ∴∠B1DF=∠OBB1. ∵∠DOA=∠BOB1=90°, ∴△AOD∽△B1OB, ∴=, ∴=, ∴OB1=. 由轴对称的性质可得AB1=AB=m﹣n. 在Rt△AOB1中, n2+()2=(m﹣n)2, 整理得3m2﹣8mn=0. ∵m>0,∴3m﹣8n=0, ∴=. 34.如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l. (1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标; (2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线l的对称点为N,试证明四边形CDAN是平行四边形; (3)点P在直线l上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标. 【分析】(1)将A、C两点坐标代入解析式即可求出a、c,将解析式配成顶点式即可得到对称轴方程和顶点坐标; (2)先由C、M两点坐标求出直线CM解析式,进而求出D点坐标,由于C、N两点关于抛物线对称轴对称,则CN∥ AD,同时可求出N点坐标,然后得出CN=AD,结论显然; (3)设出P点纵坐标,表示出MP的长度,过点P作PH⊥DM于H,表示出PH的长度,在直角三角形PAE中用勾股定理列出方程,解之即得答案. 【解答】解:(1)∵抛物线y=ax2+2x+c经过点A(﹣1,0)和点C(0,3), ∴, ∴, ∴y=﹣x2+2x+3=﹣(x﹣1)2+4, 对称轴为直线x=1,顶点M(1,4); (2)如图1, ∵点C关于直线l的对称点为N, ∴N(2,3), ∵直线y=kx+b经过C、M两点, ∴, ∴, ∴y=x+3, ∵y=x+3与x轴交于点D, ∴D(﹣3,0), ∴AD=2=CN 又∵AD∥CN, ∴CDAN是平行四边形; (3)设P(1,a),过点P作PH⊥DM于H,连接PA、PB,如图2, 则MP=4﹣a, 又∠HMP=45°, ∴HP=AP=, Rt△APE中,AP2=AE2+PE2, 即:,解得:, ∴P1(1,﹣4+2),P2(1,﹣4﹣2). 35.如图,在Rt△ABC中,∠C=90°,AC=14,tanA=,点D是边AC上一点,AD=8,点E是边AB上一点,以点E为圆心,EA为半径作圆,经过点D,点F是边AC上一动点(点F不与A、C重合),作FG⊥EF,交射线BC于点G. (1)用直尺圆规作出圆心E,并求圆E的半径长(保留作图痕迹); (2)当点G的边BC上时,设AF=x,CG=y,求y关于x的函数解析式,并写出它的定义域; (3)联结EG,当△EFG与△FCG相似时,推理判断以点G为圆心、CG为半径的圆G与圆E可能产生的各种位置关系. 【分析】 (1)由于ED=EA,因此点E在线段AD的垂直平分线上,因而线段AD的垂直平分线与线段AB的交点即为圆心E(如图1),然后只需解Rt△EHA就可解决问题; (2)如图2,易证△GCF∽△FHE,然后运用相似三角形的性质就可解决问题; (3)由于点G在射线BC上,故需分点G在线段BC上(如图2、图3),点G在线段BC的延长线上(如图4),然后只需求出CG和GE就可解决问题. 【解答】解:(1)作线段AD的垂直平分线,交AB于E,交AC于H,如图1, 点E即为所求作. 在Rt△EHA中,AH=AD=4,tanA=, ∴EH=AH•tanA=4×=3,AE==5. ∴圆E的半径长为5; (2)当点G的边BC上时,如图2所示. ∵∠C=90°,FG⊥EF,EH⊥AC, ∴∠C=∠EHF=90°,∠CFG=∠FEH=90°﹣∠EFH, ∴△GCF∽△FHE, ∴=, ∴=, ∴y=﹣x2+6x﹣(4≤x<14); (3)①当点G在BC上时, Ⅰ.当∠FGE=∠CGF时, 过点E作EN⊥BC于N,如图2, ∵∠C=∠GFE=90°, ∴△GCF∽△GFE, ∴=. ∵△GCF∽△FHE, ∴=, ∴=, ∴FC=FH=CH=(14﹣4)=5, ∴x=AF=5+4=9, ∴y=CG=, ∴rG=GC=,rE=5. ∴GN=﹣3=,EN=CH=10, ∴EG==, ∴rG﹣rE<GE<rG+rE, ∴⊙E与⊙G相交; Ⅱ.当∠FGE=∠CFG时,如图3, 则有GE∥AC, ∵∠C=∠AHE=90°,∴CG∥EH, ∴四边形CGEH是矩形, ∴rG=CG=EH=3,GE=CH=10, ∴GE>rE+rG, ∴⊙E与⊙G外离; ②当点G在BC延长线上时,设GE交AC于M,如图4, ∵∠EHF=∠GCF=90°,∠GFC=∠HEF=90°﹣∠HFE, ∴△EHF∽△FCG, ∴=, ∴=, ∴y=(x﹣4)(x﹣14). ∵∠FGE=∠CFG,∠FGE+∠MEF=90°,∠GFM+∠MFE=90°, ∴MG=MF,∠MEF=∠MFE, ∴ME=MF,∴MG=ME. 在△GCM和△EHM中, ∴△GCM≌△EHM, ∴CG=HE=3,CM=MH=5, ∴rG=3,EG=2GM=2, ∴GE>rG+rE, ∴⊙E与⊙G外离. 综上所述:当△EFG与△FCG相似时,⊙E与⊙G相交或外离. 36.如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°. 点C是弧AB上的点,联结PC、DC. (1)联结BD交弧AB于E,当a=2时,求BE的长; (2)当以PC为半径的⊙P和以CD为半径的⊙C相切时,求a的值; (3)当直线DC经过点B,且满足PC•OA=BC•OP时,求扇形OAB的半径长. 【分析】(1)如图1中,连接OE,作OM⊥BC于M.设⊙O半径为r,先列出关于r的方程求出r,再求出OM,在RT△BOM中利用勾股定理即可. (2)如图2中,⊙C与⊙P相切于点M,连接DM与⊙P交于点Q,连接PQ、CQ、OC,想分别证明点A是△CMD的重心即可. (3)如图3中,连接OC、PB、AC,想办法证明△OBC是等边三角形,再利用方程即可解决问题. 【解答】解:(1)如图1中,连接OE,作OM⊥BC于M.设⊙O半径为r, ∵OA2=OP•OD, ∴r2=(r﹣1)(r+2), ∴r=2, 在RT△BOD中,∵OB=2,OD=4, ∴BD===2, ∵•OD•OB=•BD•OM, ∴OM=, 在RT△BOM中,∵, ∴BM==, ∵OM⊥BE, ∴BM=ME,BE=2BM=. (2)如图2中,⊙C与⊙P相切于点M,连接DM与⊙P交于点Q,连接PQ、CQ、OC. ∵OA2=OP•OD, ∴OC2=OP•OD, ∴=, ∵∠COP=∠DOC, ∴△COP∽△DOC, ∴∠OCP=ODC, ∵OC=OA, ∴∠OCA=∠OAC, ∴∠OCP+∠PCA=∠ACD+∠ODC, ∴∠PCA=∠DCA, ∵CM=CD,∠CQM=90°(直径CM所对的圆周角是直角), ∴∠MCQ=∠DCQ, ∴C、A、Q共线, ∵MP=PC,MQ=QD, ∴PQ∥CD,PQ=CD, ∴PA:AD=PQ:CD=1:2, ∴AD=2PA=2. (3)如图3中,连接OC、PB、AC. ∵∵OA2=OP•OD, ∴OC2=OP•OD, ∴=, ∵∠COP=∠DOC, ∴△COP∽△DOC, ∴∠OCP=ODC, 同理△BOP∽△DOB,∠OBP=∠D, ∴∠OBP=∠OCP, ∴O、B、C、P四点共圆, ∴∠BOP+∠BCP=90°, ∵PC•OA=BC•OP, ∴=,∵∠BOP=∠BCP, ∴△PBO∽△PBC, ∴===1, ∴OB=BC=OC,PC=OP,设BO=BC=OC=r, ∴△BOC是等边三角形, ∴∠OBC=60°,∠D=30°, 在RT△PCD中,∵PC=OP=r﹣1, ∴PD=2PC=2r﹣2, ∴AD=2r﹣3, ∵OD=OB, ∴r+2r﹣3=r, ∴r=, ∴扇形OAB的半径长为. 37.如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<). (1)如图1,连接DQ平分∠BDC时,t的值为 1 ; (2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值; (3)请你继续进行探究,并解答下列问题: ①证明:在运动过程中,点O始终在QM所在直线的左侧; ②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由. 【分析】(1)先利用△PBQ∽△CBD求出PQ、BQ,再根据角平分线性质,列出方程解决问题. (2)由△QTM∽△BCD,得=列出方程即可解决. (3)①如图2中,延长QM交CD于E,求出DE、DO利用差值比较即可解决问题. ②如图3中,由①可知⊙O只有在左侧与直线QM相切于点H,QM与CD交于点E.由△OHE∽△BCD,得=,列出方程即可解决问题.利用反证法证明直线PM不可能由⊙O相切. 【解答】(1)解:如图1中,∵四边形ABCD是矩形, ∴∠A=∠C=∠ADC=∠ABC=90°,AB=CD=6.AD=BC=8, ∴BD===10, ∵PQ⊥BD, ∴∠BPQ=90°=∠C, ∵∠PBQ=∠DBC, ∴△PBQ∽△CBD, ∴==, ∴==, ∴PQ=3t,BQ=5t, ∵DQ平分∠BDC,QP⊥DB,QC⊥DC, ∴QP=QC, ∴3t=8﹣5t, ∴t=1, 故答案为:1. (补充:直接利用角平分线的性质得到DP=DC=6,BP=4,从而t=1) (2)解:如图2中,作MT⊥BC于T. ∵MC=MQ,MT⊥CQ, ∴TC=TQ, 由(1)可知TQ=(8﹣5t),QM=3t, ∵MQ∥BD, ∴∠MQT=∠DBC, ∵∠MTQ=∠BCD=90°, ∴△QTM∽△BCD, ∴=, ∴=, ∴t=(s), ∴t=s时,△CMQ是以CQ为底的等腰三角形. (3)①证明:如图2中,延长QM交CD于E, ∵EQ∥BD, ∴=, ∴EC=(8﹣5t),ED=DC﹣EC=6﹣(8﹣5t)=t, ∵DO=3t, ∴DE﹣DO=t﹣3t=t>0, ∴点O在直线QM左侧. ②解:如图3中,由①可知⊙O只有在左侧与直线QM相切于点H,QM与CD交于点E. ∵EC=(8﹣5t),DO=3t, ∴OE=6﹣3t﹣(8﹣5t)=t, ∵OH⊥MQ, ∴∠OHE=90°, ∵∠HEO=∠CEQ, ∴∠HOE=∠CQE=∠CBD, ∵∠OHE=∠C=90°, ∴△OHE∽△BCD, ∴=, ∴=, ∴t=. ∴t=s时,⊙O与直线QM相切. 连接PM,假设PM与⊙O相切,则∠OMH=PMQ=22.5°, 在MH上取一点F,使得MF=FO,则∠FMO=∠FOM=22.5°, ∴∠OFH=∠FOH=45°, ∴OH=FH=,FO=FM=, ∴MH=(+1), 由=得到HE=, 由=得到EQ=, ∴MH=MQ﹣HE﹣EQ=4﹣﹣=, ∴(+1)≠,矛盾, ∴假设不成立. ∴直线PM与⊙O不相切. 38.如图,抛物线y=﹣x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧. (1)求抛物线的解析式; (2)若PA:PB=3:1,求一次函数的解析式; (3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得⊙C同时与x轴和直线AP都相切,如果存在,请求出点C的坐标,如果不存在,请说明理由. 【分析】(1)根据抛物线的对称轴为x=1可求出m的值,再将点A的坐标代入抛物线的解析式中求出n值,此题得解; (2)根据P、A、B三点共线以及PA:PB=3:1结合点A的坐标即可得出点B的纵坐标,将其代入抛物线解析式中即可求出点B的坐标,再根据点A、B的坐标利用待定系数法即可求出直线AP的解析式; (3)假设存在,设出点C的坐标,依照题意画出图形,根据角的计算找出∠DCF=∠EPF,再通过解直角三角形找出关于r的一元一次方程,解方程求出r值,将其代入点C的坐标中即可得出结论. 【解答】解:(1)∵抛物线的对称轴为x=1, ∴﹣=1,解得:m=. 将点A(2,3)代入y=﹣x2+x+n中, 3=﹣1+1+n,解得:n=3, ∴抛物线的解析式为y=﹣x2+x+3. (2)∵P、A、B三点共线,PA:PB=3:1,且点A、B位于点P的同侧, ∴yA﹣yP=3yB﹣yP, 又∵点P为x轴上的点,点A(2,3), ∴yB=1. 当y=1时,有﹣x2+x+3=1, 解得:x1=﹣2,x2=4(舍去), ∴点B的坐标为(﹣2,1). 将点A(2,3)、B(﹣2,1)代入y=kx+b中, ,解得:, ∴一次函数的解析式y=x+2. (3)假设存在,设点C的坐标为(1,r). ∵k>0, ∴直线AP的解析式为y=x+2. 当y=0时,x+2=0, 解得:x=﹣4, ∴点P的坐标为(﹣4,0), 当x=1时,y=, ∴点D的坐标为(1,). 令⊙与直线AP的切点为F,与x轴的切点为E,抛物线的对称轴与直线AP的交点为D,连接CF,如图所示. ∵∠PFC=∠PEC=90°,∠EPF+∠ECF=∠DCF+∠ECF=180°, ∴∠DCF=∠EPF. 在Rt△CDF中,tan∠DCF=tan∠EPF=,CD=﹣r, ∴CD=CF=|r|=﹣r, 解得:r=5﹣10或r=﹣5﹣10. 故当k>0时,抛物线的对称轴上存在点C,使得⊙C同时与x轴和直线AP都相切,点C的坐标为(1,5﹣10)或(1,﹣5﹣10). 39.如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q. (1)这条抛物线的对称轴是 2 ,直线PQ与x轴所夹锐角的度数是 45° ; (2)若两个三角形面积满足S△POQ=S△PAQ,求m的值; (3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD•DQ的最大值. 【分析】(1)把抛物线的解析式化成顶点式即可求得对称轴;求得直线与坐标轴的交点坐标,即可证得直线和坐标轴围成的图形是等腰直角三角形,从而求得直线PQ与x轴所夹锐角的度数; (2)分三种情况分别讨论根据已知条件,通过△OBE∽△ABF对应边成比例即可求得; (3)①过点C作CH∥x轴交直线PQ于点H,可得△CHQ是等腰三角形,进而得出AD⊥PH,得出DQ=DH,从而得出PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,得出PH=PM,因为当PM最大时,PH最大,通过求得PM的最大值,从而求得PH的最大值;由①可知:PD+PH≤6 ,设PD=a,则DQ﹣a,得出PD•DQ≤a(6﹣a)=﹣a2+6a=﹣(a﹣3)2+18,当点P在抛物线的顶点时,a=3,得出PD•DQ≤18. 【解答】方法一: 解:(1)∵y=x2﹣4x=(x﹣2)2﹣4, ∴抛物线的对称轴是x=2, ∵直线y=x+m, ∴直线与坐标轴的交点坐标为(﹣m,0),(0,m), ∴交点到原点的距离相等, ∴直线与坐标轴围成的三角形是等腰直角三角形, ∴直线PQ与x轴所夹锐角的度数是45°, 故答案为x=2、45°. (2)如图 设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,S△POQ=S△PAQ不成立; ①当点B落在线段OA上时,如图①, ==, 由△OBE∽△ABF得,==, ∴AB=3OB, ∴OB=OA, 由y=x2﹣4x得点A(4,0), ∴OB=1, ∴B(1,0), ∴1+m=0, ∴m=﹣1; ②当点B落在线段AO的延长线上时,如图②,同理可得OB=OA=2, ∴B(﹣2,0), ∴﹣2+m=0, ∴m=2, 综上,当m=﹣1或2时,S△POQ=S△PAQ; (3)①过点C作CH∥x轴交直线PQ于点H,如图③,可得△CHQ是等腰三角形, ∵∠CDQ=45°+45°=90°, ∴AD⊥PH, ∴DQ=DH, ∴PD+DQ=PH, 过P点作PM⊥CH于点M,则△PMH是等腰直角三角形, ∴PH=PM, ∴当PM最大时,PH最大, ∴当点P在抛物线顶点处时,PM最大,此时PM=6, ∴PH的最大值为6, 即PD+DQ的最大值为6. ②由①可知:PD+DQ≤6, 设PD=a,则DQ﹣a, ∴PD•DQ≤a(6﹣a)=﹣a2+6a=﹣(a﹣3)2+18, ∵当点P在抛物线的顶点时,a=3, ∴PD•DQ≤18. ∴PD•DQ的最大值为18. 方法二: (1)略. (2)过点A作x轴垂线,与直线PQ交于点D,设直线PQ与y轴交于点C, ∴C(0,m),D(4,4+m), ∵S△POQ=(Qx﹣Px)(QY﹣CY), S△PAQ=(Qx﹣Px)(DY﹣AY), ∵, ∴, ∴m1=2,m2=﹣1. (3)①设P(t,t2﹣4t)(0<t<4), ∵KPQ=1,∴lPQ:y=x+t2﹣5t, ∵C(2,2),A(4,0), ∴lAC:y=﹣x+4, ∴DX=,DY=, ∴Q(2,t2﹣5t+2), ∵PQ⊥AC,垂足为点D, ∴点Q关于直线AC的对称点Q′(﹣t2+5t+2,2), 欲使PD+DQ取得最大值,只需PQ′有最大值, PQ′==, 显然当t=2时,PQ′的最大值为6, 即PD+DQ的最大值为6, ②∵(PD+DQ)2≥4•PD•DQ, ∴PD•DQ≤==18, ∴PD•DQ的最大值为18. 40.抛物线y=ax2+bx+4(a≠0)过点A(1,﹣1),B(5,﹣1),与y轴交于点C. (1)求抛物线的函数表达式; (2)如图1,连接CB,以CB为边作▱CBPQ,若点P在直线BC上方的抛物线上,Q为坐标平面内的一点,且▱CBPQ的面积为30,求点P的坐标; (3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值. 【分析】(1)将点A、B的坐标代入抛物线的解析式,得到关于a、b的方程,从而可求得a、b的值; (2)设点P的坐标为P(m,m2﹣6m+4),由平行四边形的面积为30可知S△CBP=15,由S△CBP=S梯形CEDP﹣S△CEB﹣S△PBD,得到关于m的方程求得m的值,从而可求得点P的坐标; (3)首先证明△EAB∽△NMB,从而可得到NB=,当MB为圆的直径时,NB有最大值. 【解答】解:(1)将点A、B的坐标代入抛物线的解析式得:, 解得:. ∴抛物线得解析式为y=x2﹣6x+4. (2)如图所示: 设点P的坐标为P(m,m2﹣6m+4) ∵平行四边形的面积为30, ∴S△CBP=15,即:S△CBP=S梯形CEDP﹣S△CEB﹣S△PBD. ∴m(5+m2﹣6m+4+1)﹣×5×5﹣(m﹣5)(m2﹣6m+5)=15. 化简得:m2﹣5m﹣6=0, 解得:m=6,或m=﹣1. ∴点P的坐标为(6,4)或(﹣1,11). (3)连接AB、EB. ∵AE是圆的直径, ∴∠ABE=90°. ∴∠ABE=∠MBN. 又∵∠EAB=∠EMB, ∴△EAB∽△NMB. ∵A(1,﹣1),B(5,﹣1), ∴点O1的横坐标为3, 将x=0代入抛物线的解析式得:y=4, ∴点C的坐标为(0,4). 设点O1的坐标为(3,m), ∵O1C=O1A, ∴, 解得:m=2, ∴点O1的坐标为(3,2), ∴O1A=, 在Rt△ABE中,由勾股定理得:BE===6, ∴点E的坐标为(5,5). ∴AB=4,BE=6. ∵△EAB∽△NMB, ∴. ∴. ∴NB=. ∴当MB为直径时,MB最大,此时NB最大. ∴MB=AE=2, ∴NB==3. 41.如图,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12. (1)如图①,点M是四边形ABCD边AD上的一点,则△BMC的面积为 24 ; (2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值; (3)如图③,在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由. 【分析】(1)如图①,过A作AE⊥ BC,可得出四边形AECD为矩形,得到EC=AD,BE=BC﹣EC,在直角三角形ABE中,求出AE的长,即为三角形BMC的高,求出三角形BMC面积即可; (2)如图②,作点C关于直线AD的对称点C′,连接C′N,C′D,C′B交AD于点N′,连接CN′,则BN+NC=BN+NC′≥BC′=BN′+CN′,可得出△BNC周长的最小值为△BN′C的周长=BN′+CN′+BC=BC′+BC,求出即可; (3)如图③所示,存在点P,使得cos∠BPC的值最小,作BC的中垂线PQ交BC于点Q,交AD于点P,连接BP,CP,作△BPC的外接圆O,圆O与直线PQ交于点N,则PB=PC,圆心O在PN上,根据AD与BC平行,得到圆O与AD相切,根据PQ=DC,判断得到PQ大于BQ,可得出圆心O在BC上方,在AD上任取一点P′,连接P′B,P′C,P′B交圆O于点M,连接MC,可得∠BPC=∠BMC≥∠BP′C,即∠BPC最大,cos∠BPC的值最小,连接OB,求出即可. 【解答】解:(1)如图①,过A作AE⊥BC, ∴四边形AECD为矩形, ∴EC=AD=8,BE=BC﹣EC=12﹣8=4, 在Rt△ABE中,∠ABE=60°,BE=4, ∴AB=2BE=8,AE==4, 则S△BMC=BC•AE=24; 故答案为:24; (2)如图②,作点C关于直线AD的对称点C′,连接C′N,C′D,C′B交AD于点N′,连接CN′,则BN+NC=BN+NC′≥BC′=BN′+CN′, ∴△BNC周长的最小值为△BN′C的周长=BN′+CN′+BC=BC′+BC, ∵AD∥BC,AE⊥BC,∠ABC=60°, ∴过点A作AE⊥BC,则CE=AD=8, ∴BE=4,AE=BE•tan60°=4, ∴CC′=2CD=2AE=8, ∵BC=12, ∴BC′==4, ∴△BNC周长的最小值为4+12; (3)如图③所示,存在点P,使得cos∠BPC的值最小, 作BC的中垂线PQ交BC于点Q,交AD于点P,连接BP,CP,作△BPC的外接圆O,圆O与直线PQ交于点N,则PB=PC,圆心O在PN上, ∵AD∥BC, ∴圆O与AD相切于点P, ∵PQ=DC=4>6, ∴PQ>BQ, ∴∠BPC<90°,圆心O在弦BC的上方, 在AD上任取一点P′,连接P′B,P′C,P′B交圆O于点M,连接MC, ∴∠BPC=∠BMC≥∠BP′C, ∴∠BPC最大,cos∠BPC的值最小, 连接OB,则∠BON=2∠BPN=∠BPC, ∵OB=OP=4﹣OQ, 在Rt△BOQ中,根据勾股定理得:OQ2+62=(4﹣OQ)2, 解得:OQ=, ∴OB=, ∴cos∠BPC=cos∠BOQ==, 则此时cos∠BPC的值为. 42.如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4,∠BAD=60°,且AB>4. (1)求∠EPF的大小; (2)若AP=6,求AE+AF的值; (3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值. 【分析】(1)过点P作PG⊥EF于G,解直角三角形即可得到结论; (2)如图2,过点P作PM⊥AB于M,PN⊥AD于N,证明△ABC≌△ADC,Rt△PME≌Rt△PNF,问题即可得证; (3)如图3,当EF⊥AC,点P在EF的右侧时,AP有最大值,当EF⊥AC,点P在EF的左侧时,AP有最小值解直角三角形即可解决问题. 【解答】解:(1)如图1,过点P作PG⊥EF于G, ∵PE=PF, ∴FG=EG=EF=2,∠FPG=, 在△FPG中,sin∠FPG===, ∴∠FPG=60°, ∴∠EPF=2∠FPG=120°; (2)如图2,过点P作PM⊥AB于M,PN⊥AD于N, ∵四边形ABCD是菱形, ∴AD=AB,DC=BC, ∴∠DAC=∠BAC, ∴PM=PN, 在Rt△PME于Rt△PNF中, , ∴Rt△PME≌Rt△PNF, ∴FN=EM,在Rt△PMA中,∠PMA=90°,∠PAM=∠DAB=30°, ∴AM=AP•cos30°=3,同理AN=3, ∴AE+AF=(AM﹣EM)+(AN+NF)=6; (3)如图3,当EF⊥AC,点P在EF的右侧时,AP有最大值, 当EF⊥AC,点P在EF的左侧时,AP有最小值, 设AC与EF交于点O, ∵PE=PF, ∴OF=EF=2, ∵∠FPA=60°, ∴OP=2, ∵∠BAD=60°, ∴∠FAO=30°, ∴AO=6, ∴AP=AO+PO=8, 同理AP′=AO﹣OP=4, ∴AP的最大值是8,最小值是4. 43.如图,在平面直角坐标系中,抛物线y=﹣x2﹣x+ 2与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D. (1)填空:点A的坐标为( 0 , 2 ),点B的坐标为( ﹣3 , 0 ),点C的坐标为( 1 , 0 ),点D的坐标为( ﹣1 , ); (2)点P是线段BC上的动点(点P不与点B、C重合) ①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标; ②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长; ③若点Q是线段AB上的动点(点Q不与点A、B重合),点R是线段AC上的动点(点R不与点A、C重合),请直接写出△PQR周长的最小值. 【分析】(1)令x=0,求得A(0,2),令y=0,求得B(﹣3,0),C(1,0),由y=﹣x2﹣x+2转化成顶点式可知D(﹣1,); (2)①设P(n,0),则E(n,﹣n2﹣n+2),根据已知条件得出﹣n2﹣n+2=1﹣n,解方程即可求得E的坐标; ②根据直线ED和EA的斜率可知直线与坐标轴的交角相等,从而求得与坐标轴构成的三角形是等腰三角形,根据等腰三角形的性质即可求得EF的长; ③根据题意得:当△PQR为△ABC垂足三角形时,周长最小,所以P与O重合时,周长最小,作O关于AB的对称点E,作O关于AC的对称点F,连接EF交AB于Q,交AC于R,此时△PQR的周长PQ+QR+PR=EF,然后求得E、F的坐标,根据勾股定理即可求得. 【解答】解:(1)令x=0,则y=2, ∴A(0,2), 令y=0,则﹣x2﹣x+2=0,解得x1=﹣3,x2=1(舍去), ∴B(﹣3,0),C(1,0), 由y=﹣x2﹣x+2=﹣(x+1)2+可知D(﹣1,), 故答案为:0、2,﹣3、0,1、0,﹣1、; (2)①设P(n,0),则E(n,﹣n2﹣n+2), ∵PE=PC, ∴﹣n2﹣n+2=1﹣n,解得n1=﹣,n2=1(舍去), ∴当n=﹣时,1﹣n=, ∴E(﹣,), ②如图1,设直线DE与x轴交于M,与y轴交于N,直线EA与x轴交于K, 根据E、D的坐标求得直线ED的斜率为,根据E、A的坐标求得直线EA的斜率为﹣, ∴△MEK是以MK为底边的等腰三角形,△AEN是以AN为底边的等腰三角形, ∵到EA和ED的距离相等的点F在顶角的平分线上, 根据等腰三角形的性质可知,EF是E点到坐标轴的距离, ∴EF=或; (3)根据题意得:当△PQR为△ABC垂足三角形时,周长最小,所以P与O重合时,周长最小, 如图2,作O关于AB的对称点E,作O关于AC的对称点F,连接EF交AB于Q,交AC于R, 此时△PQR的周长PQ+QR+PR=EF, ∵A(0,2),B(﹣3,0),C(1,0), ∴AB==,AC==, ∵S△AOB=×OE×AB=OA•OB, ∴OE=, ∵△OEM∽△ABO, ∴==,即==, ∴OM=,EM= ∴E(﹣,), 同理求得F(,), 即△PQR周长的最小值为EF==. 44.如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM. (1)当AN平分∠MAB时,求DM的长; (2)连接BN,当DM=1时,求△ABN的面积; (3)当射线BN交线段CD于点F时,求DF的最大值. 【分析】(1)由折叠性质得∠MAN=∠DAM,证出∠DAM=∠MAN=∠NAB,由三角函数得出DM=AD•tan∠DAM=即可; (2)延长MN交AB延长线于点Q,由矩形的性质得出∠DMA=∠MAQ,由折叠性质得出∠DMA=∠AMQ,AN=AD=3,MN=MD=1,得出∠MAQ=∠AMQ,证出MQ=AQ,设NQ=x,则AQ=MQ=1+x,证出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=4,AQ=5,即可求出△ABN的面积; (3)过点A作AH⊥BF于点H,证明△ABH∽△BFC,得出对应边成比例=,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果. 【解答】解:(1)由折叠性质得:△ANM≌△ADM, ∴∠MAN=∠DAM, ∵AN平分∠MAB,∠MAN=∠NAB, ∴∠DAM=∠MAN=∠NAB, ∵四边形ABCD是矩形, ∴∠DAB=90°, ∴∠DAM=30°, ∴DM=AD•tan∠DAM=3×tan30°=3×=; (2)延长MN交AB延长线于点Q,如图1所示: ∵四边形ABCD是矩形, ∴AB∥DC, ∴∠DMA=∠MAQ, 由折叠性质得:△ANM≌△ADM, ∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1, ∴∠MAQ=∠AMQ, ∴MQ=AQ, 设NQ=x,则AQ=MQ=1+x, ∵∠ANM=90°, ∴∠ANQ=90°, 在Rt△ANQ中,由勾股定理得:AQ2=AN2+NQ2, ∴(x+1)2=32+x2, 解得:x=4, ∴NQ=4,AQ=5, ∵AB=4,AQ=5, ∴S△NAB=S△NAQ=×AN•NQ=××3×4=; (3)过点A作AH⊥BF于点H,如图2所示: ∵四边形ABCD是矩形, ∴AB∥DC, ∴∠HBA=∠BFC, ∵∠AHB=∠BCF=90°, ∴△ABH∽△BFC, ∴=, ∵AH≤AN=3,AB=4, ∴当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图3所示: 由折叠性质得:AD=AH, ∵AD=BC, ∴AH=BC, 在△ABH和△BFC中,, ∴△ABH≌△BFC(AAS), ∴CF=BH, 由勾股定理得:BH===, ∴CF=, ∴DF的最大值=DC﹣CF=4﹣. 45.如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在上且不与A点重合,但Q点可与B点重合. 发现:的长与的长之和为定值l,求l: 思考:点M与AB的最大距离为 ,此时点P,A间的距离为 2 ; 点M与AB的最小距离为 ,此时半圆M的弧与AB所围成的封闭图形面积为 ﹣ ; 探究:当半圆M与AB相切时,求的长. (注:结果保留π,cos35°=,cos55°=) 【分析】(1)半圆O的长度是固定不变的,由于PQ也是定值,所以的长度也是固定值,所以与的长之和为定值; (2)过点M作MC⊥AB于点C,当C与O重合时,M与AB的距离最大,此时,∠AOP=60°,AP=2;当Q与B重合时,M与AB的距离最小,此时围成的封闭图形面积可以用扇形DMB的面积减去△DMB的面积即可; (3)当半圆M与AB相切时,此时MC=1,且分以下两种情况讨论,当C在线段OA上;当C在线段OB上,然后分别计出的长. 【解答】解:发现:如图1,连接OP、OQ, ∵AB=4, ∴OP=OQ=2, ∵PQ=2, ∴△OPQ是等边三角形, ∴∠POQ=60°, ∴==, 又∵半圆O的长为:π×4=2π, ∴+=2π﹣π=, ∴l=π; 思考:如图2,过点M作MC⊥AB于点C, 连接OM, ∵OP=2,PM=1, ∴由勾股定理可知:OM=, 当C与O重合时, M与AB的距离最大,最大值为, 连接AP, 此时,OM⊥AB, ∴∠AOP=60°, ∵OA=OP, ∴△AOP是等边三角形, ∴AP=2, 如图3,当Q与B重合时, 连接DM, ∵∠MOQ=30°, ∴MC=OM=, 此时,M与AB的距离最小,最小值为, 设此时半圆M与AB交于点D, DM=MB=1, ∵∠ABP=60°, ∴△DMB是等边三角形, ∴∠DMB=60°, ∴扇形DMB的面积为:=, △DMB的面积为:MC•DB=××1=, ∴半圆M的弧与AB所围成的封闭图形面积为:﹣; 探究:当半圆M与AB相切时, 此时,MC=1, 如图4,当点C在线段OA上时, 在Rt△OCM中, 由勾股定理可求得:OC=, ∴cos∠AOM==, ∴∠AOM=35°, ∵∠POM=30°, ∴∠AOP=∠AOM﹣∠POM=5°, ∴==, 当点C在线段OB上时, 此时,∠BOM=35°, ∵∠POM=30°, ∴∠AOP=180°﹣∠POM﹣∠BOM=115° ∴==, 综上所述,当半圆M与AB相切时,的长为或. 46.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b. 填空:当点A位于 CB的延长线上 时,线段AC的长取得最大值,且最大值为 a+b (用含a,b的式子表示) (2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE. ①请找出图中与BE相等的线段,并说明理由; ②直接写出线段BE长的最大值. (3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标. 【分析】(1)根据点A位于CB的延长线上时,线段AC的长取得最大值,即可得到结论; (2)①根据等边三角形的性质得到AD=AB,AC=AE,∠BAD=∠CAE=60°,推出△CAD≌△EAB,根据全等三角形的性质得到CD=BE;②由于线段BE长的最大值=线段CD的最大值,根据(1)中的结论即可得到结果; (3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,得到△APN是等腰直角三角形,根据全等三角形的性质得到PN=PA=2,BN=AM,根据当N在线段BA的延长线时,线段BN取得最大值,即可得到最大值为2+3;如图2,过P作PE⊥x轴于E,根据等腰直角三角形的性质即可得到结论. 【解答】解:(1)∵点A为线段BC外一动点,且BC=a,AB=b, ∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b, 故答案为:CB的延长线上,a+b; (2)①CD=BE, 理由:∵△ABD与△ACE是等边三角形, ∴AD=AB,AC=AE,∠BAD=∠CAE=60°, ∴∠BAD+∠BAC=∠CAE+∠BAC, 即∠CAD=∠EAB, 在△CAD与△EAB中,, ∴△CAD≌△EAB, ∴CD=BE; ②∵线段BE长的最大值=线段CD的最大值, 由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上, ∴最大值为BD+BC=AB+BC=4; (3)连接BM,∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN, 则△APN是等腰直角三角形, ∴PN=PA=2,BN=AM, ∵A的坐标为(2,0),点B的坐标为(5,0), ∴OA=2,OB=5, ∴AB=3, ∴线段AM长的最大值=线段BN长的最大值, ∴当N在线段BA的延长线时,线段BN取得最大值, 最大值=AB+AN, ∵AN=AP=2, ∴最大值为2+3; 如图2,过P作PE⊥x轴于E, ∵△APN是等腰直角三角形, ∴PE=AE=, ∴OE=BO﹣AB﹣AE=5﹣3﹣=2﹣, ∴P(2﹣,). 47.如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B. (1)求该抛物线的函数表达式; (2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值; (3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′. ①写出点M′的坐标; ②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数). 【分析】(1)利用直线l的解析式求出B点坐标,再把B点坐标代入二次函数解析式即可求出a的值; (2)设M的坐标为(m,﹣m2+2m+3),然后根据面积关系将△ABM的面积进行转化; (3)①由(2)可知m=,代入二次函数解析式即可求出纵坐标的值; ②可将求d1+d2最大值转化为求AC的最小值. 【解答】解:(1)令x=0代入y=﹣3x+3, ∴y=3, ∴B(0,3), 把B(0,3)代入y=ax2﹣2ax+a+4, ∴3=a+4, ∴a=﹣1, ∴二次函数解析式为:y=﹣x2+2x+3; (2)令y=0代入y=﹣x2+2x+3, ∴0=﹣x2+2x+3, ∴x=﹣1或3, ∴抛物线与x轴的交点横坐标为﹣1和3, ∵M在抛物线上,且在第一象限内, ∴0<m<3, 令y=0代入y=﹣3x+3, ∴x=1, ∴A的坐标为(1,0), 由题意知:M的坐标为(m,﹣m2+2m+3), S=S四边形OAMB﹣S△AOB =S△OBM+S△OAM﹣S△AOB =×m×3+×1×(﹣m2+2m+3)﹣×1×3 =﹣(m﹣)2+ ∴当m=时,S取得最大值. (3)①由(2)可知:M′的坐标为(,); ②过点M′作直线l1∥l′,过点B作BF⊥l1于点F, 根据题意知:d1+d2=BF, 此时只要求出BF的最大值即可, ∵∠BFM′=90°, ∴点F在以BM′为直径的圆上, 设直线AM′与该圆相交于点H, ∵点C在线段BM′上, ∴F在优弧上, ∴当F与M′重合时, BF可取得最大值, 此时BM′⊥l1, ∵A(1,0),B(0,3),M′(,), ∴由勾股定理可求得:AB=,M′B=,M′A=, 过点M′作M′G⊥AB于点G, 设BG=x, ∴由勾股定理可得:M′B2﹣BG2=M′A2﹣AG2, ∴﹣(﹣x)2=﹣x2, ∴x=, cos∠M′BG==, ∵l1∥l′, ∴∠BCA=90°, ∠BAC=45° 方法二:过B点作BD垂直于l′于D点,过M′点作M′E垂直于l′于E点,则BD=d1,ME=d2, ∵S△ABM′=×AC×(d1+d2) 当d1+d2取得最大值时,AC应该取得最小值,当AC⊥BM′时取得最小值. 根据B(0,3)和M′(,)可得BM′=, ∵S△ABM=×AC×BM′=,∴AC=, 当AC⊥BM′时,cos∠BAC===, ∴∠BAC=45°. 48.如图,在平面直角坐标系xOy中,将二次函数y=x2﹣1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N. (1)求N的函数表达式; (2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值; (3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数. 【分析】(1)根据二次函数N的图象是由二次函数M翻折、平移得到所以a=﹣1,求出二次函数N的顶点坐标即可解决问题. (2)由PA2+PB2=(m+1)2+n2+(m﹣1)2+n2=2(m2+n2)+2=2•PO2+2可知OP最大时,PA2+PB2最大,求出OP的最大值即可解决问题. (3)画出函数图象即可解决问题. 【解答】(1)解:二次函数y=x2 ﹣1的图象M沿x轴翻折得到函数的解析式为y=﹣x2+1,此时顶点坐标(0,1), 将此图象向右平移2个单位长度后再向上平移8个单位长度得到二次函数图象N的顶点为(2,9), 故N的函数表达式y=﹣(x﹣2)2+9=﹣x2+4x+5. (2)∵A(﹣1,0),B(1,0), ∴PA2+PB2=(m+1)2+n2+(m﹣1)2+n2=2(m2+n2)+2=2•PO2+2, ∴当PO最大时PA2+PB2最大.如图,延长OC与⊙C交于点P,此时OP最大, ∴OP的最大值=OC+PC=+1, ∴PA2+PB2最大值=2(+1)2+2=38+4. (3)M与N所围成封闭图形如图所示, 由图象可知,M与N所围成封闭图形内(包括边界)整点的个数为25个. 49.如图,顶点为A(,1)的抛物线经过坐标原点O,与x轴交于点B. (1)求抛物线对应的二次函数的表达式; (2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB; (3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标. 【分析】(1)用待定系数法求出抛物线解析式, (2)先求出直线OA对应的一次函数的表达式为y=x.再求出直线BD的表达式为y=x﹣2.最后求出交点坐标C,D即可; (3)先判断出C'D与x轴的交点即为点P,它使得△ PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可. 【解答】解:(1)∵抛物线顶点为A(,1), 设抛物线解析式为y=a(x﹣)2+1, 将原点坐标(0,0)在抛物线上, ∴0=a()2+1 ∴a=﹣. ∴抛物线的表达式为:y=﹣x2+x. (2)令y=0,得 0=﹣x2+x, ∴x=0(舍),或x=2 ∴B点坐标为:(2,0), 设直线OA的表达式为y=kx, ∵A(,1)在直线OA上, ∴k=1, ∴k=, ∴直线OA对应的一次函数的表达式为y=x. ∵BD∥AO, 设直线BD对应的一次函数的表达式为y=x+b, ∵B(2,0)在直线BD上, ∴0=×2+b, ∴b=﹣2, ∴直线BD的表达式为y=x﹣2. 由 得交点D的坐标为(﹣,﹣3), 令x=0得,y=﹣2, ∴C点的坐标为(0,﹣2), 由勾股定理,得:OA=2=OC,AB=2=CD,OB=2=OD. 在△OAB与△OCD中, , ∴△OAB≌△OCD. (3)点C关于x轴的对称点C'的坐标为(0,2), ∴C'D与x轴的交点即为点P,它使得△PCD的周长最小. 过点D作DQ⊥y,垂足为Q, ∴PO∥DQ. ∴△C'PO∽△C'DQ. ∴, ∴, ∴PO=, ∴点P的坐标为(﹣,0). 查看更多