- 2021-04-23 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
用分离常数法解高考的题
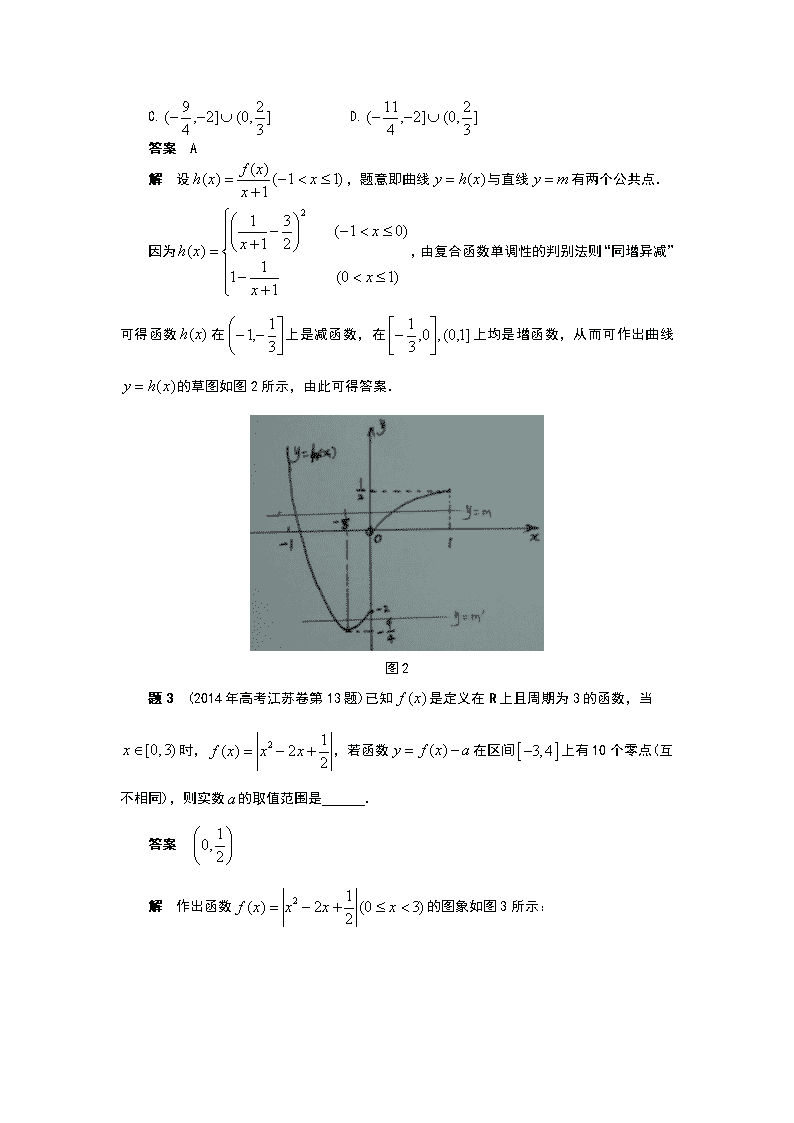
用分离常数法解2014年高考题 1 用分离常数法讨论方程根的个数 题1 (2014年高考课标全国卷I理科第11题即文科第12题)已知函数,若存在唯一的零点,且,则的取值范围是( ) A. B. C. D. 答案 C 解 因为函数的零点不为0,所以可得本题的题干等价于“关于的方程有唯一实根,且该实根是正数,求的取值范围”,也等价于“关于的方程有唯一实根,且该实根是正数,求的取值范围”. 用导数容易作出曲线如图1所示: 图1 由图1可得答案C. 题2 (2014年重庆卷文科第10题)已知函数,且在内有且仅有两个不同的零点,则实数的取值范围是( ) A. B. C. D. 答案 A 解 设,题意即曲线与直线有两个公共点. 因为,由复合函数单调性的判别法则“同增异减”可得函数在上是减函数,在上均是增函数,从而可作出曲线的草图如图2所示,由此可得答案. 图2 题3 (2014年高考江苏卷第13题)已知是定义在R上且周期为3的函数,当时,,若函数在区间上有10个零点(互不相同),则实数的取值范围是 . 答案 解 作出函数的图象如图3所示: 图3 有;当且仅当时,;. 关于方程即在上有10个零点,即曲线与直线在上有10个交点.因为函数的周期为3,所以直线与曲线有4个交点,得所求实数的取值范围是. 题4 (2014年高考天津卷理科第14题)已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为________. 答案 (0,1)∪(9,+∞) 解 因为不是原方程的根,所以设后可得本题等价于: 若关于的方程恰有4个互异的实根,则实数a的取值范围为________. (1)作出对勾函数的图象如图4所示: 图4 (2)再由平移可作出函数的图象如图5所示: 图5 (3)作出函数的图象如图6所示: 图6 因为关于的方程的互异实根个数即两条曲线公共点的个数,所以由图6可得结论: ①当时,原方程互异实根的个数是0; ②当或时,原方程互异实根的个数是2; ③当或9时,原方程互异实根的个数是3; ④当或时,原方程互异实根的个数是4. 所以本题的答案是(0,1)∪(9,+∞). 题5 (2014年高考天津卷文科第14题)已知函数f(x)=若函数y=f(x)-a|x|恰有4个零点,则实数a的取值范围为________. 答案 (1,2) 简解 因为不是函数y=f(x)-a|x|的零点,所以可得本题等价于: 若两条曲线恰有4个公共点,则实数a的取值范围为________. 同题4的解法,可作出曲线如图7所示: 图7 由图7可得结论: ①当时,原方程互异实根的个数是0; ②当或时,原方程互异实根的个数是3; ③当时,原方程互异实根的个数是6; ④当时,原方程互异实根的个数是5; ⑤当时,原方程互异实根的个数是4. 所以本题的答案是(1,2). 题6 (2014年高考天津卷理科第20(1)题)设f(x)=x-aex(a∈R),x∈R.已知函数y=f(x)有两个零点x1,x2,且x1查看更多