- 2021-04-22 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
四川省成都七中2019-2020学年高二下学期半期考试数学(理)试题答案
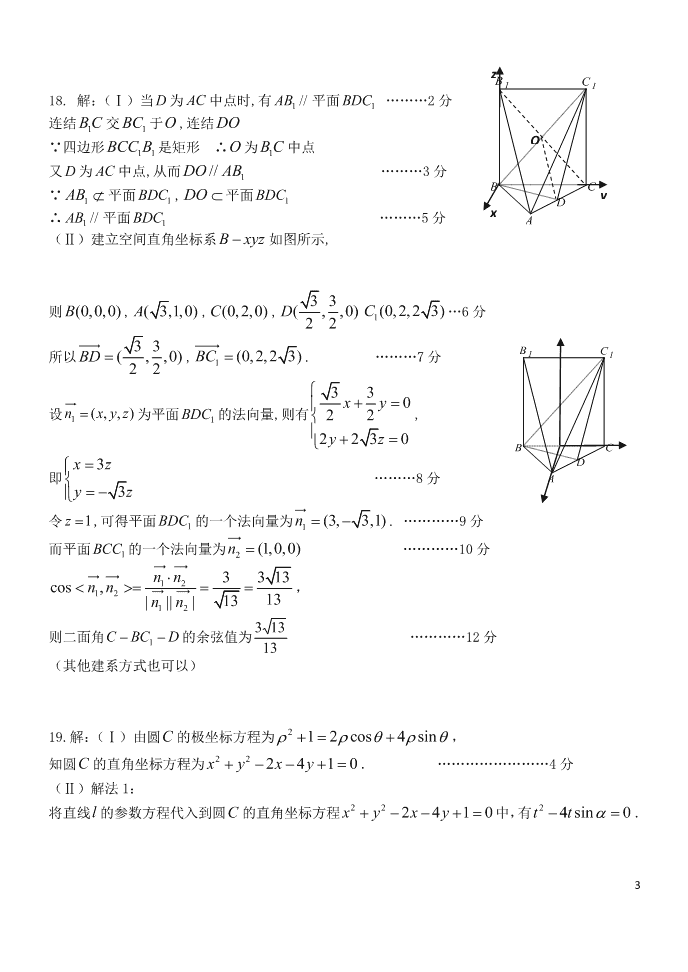
1 成都七中 2019~2020 学年度下期 2021 届高二半期考试 数学试卷(理科)答案 一、 选择题:本大题共 12 小题,每小题 5 分,共 60 分.在每小题列出的四个选项中,选出 符合题目要求的一项. 1 2 3 4 5 6 7 8 9 10 11 12 B B D C B C D D A A D B 12.解:由 fx的极值为 3 2 0 3fx, 00 0 3 cos0 2 xxfxkkZ mmm 00 0 111,2222 xx mkkZkxmm 222222222 0000 33.3322.444 mmmxf xxf xmmmm 或 二、填空题:本大题共 4 小题,每小题 5 分,共 20 分. 13. 50 14. ,4 说明:不写为集合的形式扣 2 分 15. 1,0 e 16. 33 42 , 16.解:由 232 0 ,.3fxxaxaxR 3002ffa 当 30 2x a , 时, 0;fx 当 3 ,2x a 时, 0.fx 设集合 12, , 1, , 0 ,A f x x B x f xfx 若对任意的 1 2,x ,都存在 2 1,x ,使得 121f x f x,等价于 .AB 显然0.B ①当 332, 024aa 即 时,由 3 02f a ,知0 ,0AB,不满足 AB ; 2 ② 当 33312, 242 aa 即 时 , 由 20f , 且此时 fx 在 2, 上递减, , 2 ,0 .A f A 由 10f ,得 在 1, 上取值范围包含 ,0 .AB ③ 当 331,22aa 即 时 , 由 10f , 且此时 在 1, 上递减, 1 ,0,,2,1BAf f 不满足 AB . 综上, 33.42a , 三、解答题:(本大题共 6 小题,共 70 分.其中 17 题 10 分,18—22 题每小题 12 分) 17.解:(Ⅰ)由函数 311() 32f x x ,则 2()f x x . 曲线 ()yfx 在点 51, 6P 处的切线斜率 11,kf 故切线方程为 5 1,6610.6yxxy 故所求三角形的面积 1 1 1 1 .2 6 6 72S ………5 分 (Ⅱ)由点 12, 2A 及 ,则 811(2) 322f , 不妨设切点为 00,Pxy ,则 2 00 00 3 00 00 00 0311 1 1932 221 22 k f x x xx yx yy y k x 或 …………8 分 故切线方程为 1 182350.2yxy或 …………10 分 (漏解扣 2 分) 3 18. 解:(Ⅰ)当 D 为 AC 中点时,有 //1AB 平面 1BDC ………2 分 连结 1BC交 1BC 于O ,连结 DO ∵四边形 11BCC B 是矩形 ∴ 为 中点 又 为 中点,从而 1//DO AB ………3 分 ∵ 1AB 平面 , DO 平面 ∴ 平面 ………5 分 (Ⅱ)建立空间直角坐标系 B x y z 如图所示, 则 (0 ,0 ,0 )B , ( 3,1,0 )A , (0 ,2 ,0 )C , 33( , ,0)22D 1 (0 ,2 ,2 3)C …6 分 所以 33( , ,0)22BD , 1 (0,2,23)BC . ………7 分 设 为平面 的法向量,则有 33022 2230 xy yz , 即 3 3 xz yz ………8 分 令 1z ,可得平面 的一个法向量为 1 (3,3,1)n . …………9 分 而平面 1B C C 的一个法向量为 2 (1,0,0)n …………10 分 12 12 12 33 13cos, 1313|||| nnnn nn , 则二面角 DBCC 1 的余弦值为 13 133 …………12 分 (其他建系方式也可以) 19.解:(Ⅰ)由圆C 的极坐标方程为 2 1 2 cos 4 sin , 知圆 的直角坐标方程为 222 4 1 0x y x y . ……………………4 分 (Ⅱ)解法 1: 将直线l 的参数方程代入到圆 的直角坐标方程 中,有 2 4 sin 0tt. ),,(1 zyxn C1B1 D CB A O y x z 4 设 AB、 两点对应的参数分别为 12,tt,则 12 12 4sin 0 tt tt . ……………………8 分 由 2 1 2 1 2 1 2 1 24 4sin 2 3AB t t t t t t t t , 得 32sin. 233 或 ……………………12 分 解法 2:化为直角坐标方程求解. 20.解:(Ⅰ)由题意可知, ,0.1 xgxx x 由已知 1 2 1 3 1, , ,1 1 1 2 1 311 x x x x xxg x g x g g x g g xxx x x x x , 猜想 ,.1n xgxnN nx ……………………2 分 下面用数学归纳法证明. ①当 1n 时, 1 1 xgx x ,结论成立; ……………………1 分 ②假设 1,nkkkN 时结论成立,即 .1k xgx kx 那么,当 11,nkkkN 时, 1 1 111 1 1 k kk k x gx xkxgxg gx xgxkx kx ,即结论成立. 由①②可知,结论对 nN 成立. ……………………6 分 (Ⅱ)证明: ,0.1 xg xx x 2 2 1111 111 xg xg n xxn . ……………………8 分 5 2222 2222 2222 2 1121311 11111111123 1111 123 1111 1223341 111111 12231 11 1 ggggn n n n n nn n nn nn nn .1 ……………………12 分 21.解:(Ⅰ) 21ln1 2fxaxaxxaR ,定义域为 0, . 11,0. xaxafxaxx xx ……………………1 分 令 0fx ,则 12,1.xax ①当 0a 时,令 0fx ,则 01x;令 0fx ,则 1.x fx 在 0 ,1 上单调递增;在 1, 上单调递减. ②当 01a时,令 ,则 1ax;令 ,则 0 xa或 在 0, a , 上单调递减;在 ,1a 上单调递增. ③当 1a 时,令 0fx ,则 fx在 0, 上单调递减. ④当 1a 时,令 ,则1 xa;令 ,则01x或 .xa 在 0,1 , ,a 上单调递减;在 1, a 上单调递增. ……………5 分 综上所述,①当 时, fx在 上单调递增;在 上单调递减. ②当 时, fx在 , 上单调递减;在 上单调递增. ③当 时, 在 上单调递减. ④当 时, fx在 , 上单调递减;在 上单调递增. ………6 分 (Ⅱ) 21ln 1 2f x a x a x x 且当 0a 时, 21 2f x x ax b 恒成立 6 lnb a x x 恒成立 ………………7 分 令 ln,0gxaxxx ,即 min .b g x 10,axagxa xx gx 在 0,a 上单调递减;在 ,a 上单调递增, min ln.gxgaaaa 1ln , ,12b a a a a . ………………9 分 令 1ln,,1, 2haaaaa ln0,haaha 在 1 ,12 上单调递增, min 1ln 21ln 21 ,222h ahb ,即 b 的最大值为 l n 2 1 2 . ……………12 分 22.解:(Ⅰ)当 1a 时, ln0 xefxxxx x 22 1 111. x xex xfxex xxx ……………1 分 令 xhxex ,则当 0,x 时, 10xhxe , 0, 0 1, .xh x h e x 在 上, 即 ……………2 分 (未证明,扣 1 分) 令 0,fx 则 1x ,经检验,在 0 ,1 上 0fx , fx单调递减;在 1, 上 0fx , 单调递增.当 时,函数 y f x 取得极小值 1e ,无极大值. ……………4 分 (未注明无极大值,扣 1 分) (Ⅱ) 2 1 1 0 xexf x a xxx , 令 2 1 1( ) 0 xexp x f x a xxx , 则 2 3 22 0. xe x x x p x xx ………………6 分 7 由(Ⅰ)知,当 0,x 时, ,xex 222222210xexxxxxxxxx , 2 3 22 00 xe x x x p x xx fx 为定义域上的增函数. 22111,110,204242 eeafafa 方程 0fx 在 0, 上有唯一解. ………………8 分 设 的解为 0x ,则在 00, x 上 0fx ,在 0 ,x 上 0fx ,且 01 2 . x fx 的最小值 0 000 0 ln xegafxaxx x . 由 0 0fx ,得 0 0 2 00 1 1 , xexa xx 代入 ga得, 000 00 000 02 0000 121 ln1 ln1,2 . xxx exexeg axxx xxxxx ……10 分 令 2 1 ln 1,2 xexx x xx ,则 2 2 22 . xexxx x x 22 2 2 1 1 1x x x 2 220,xxexxxxe 故 x 为 1,2 上的减函数. 21ln 21,1 .xg ae, ……12 分查看更多