山东省实验中学2019届高三第四次模拟数学（文）试题（PDF版）

山东省实验中学2019届高三第四次模拟数学（文）试题（PDF版）

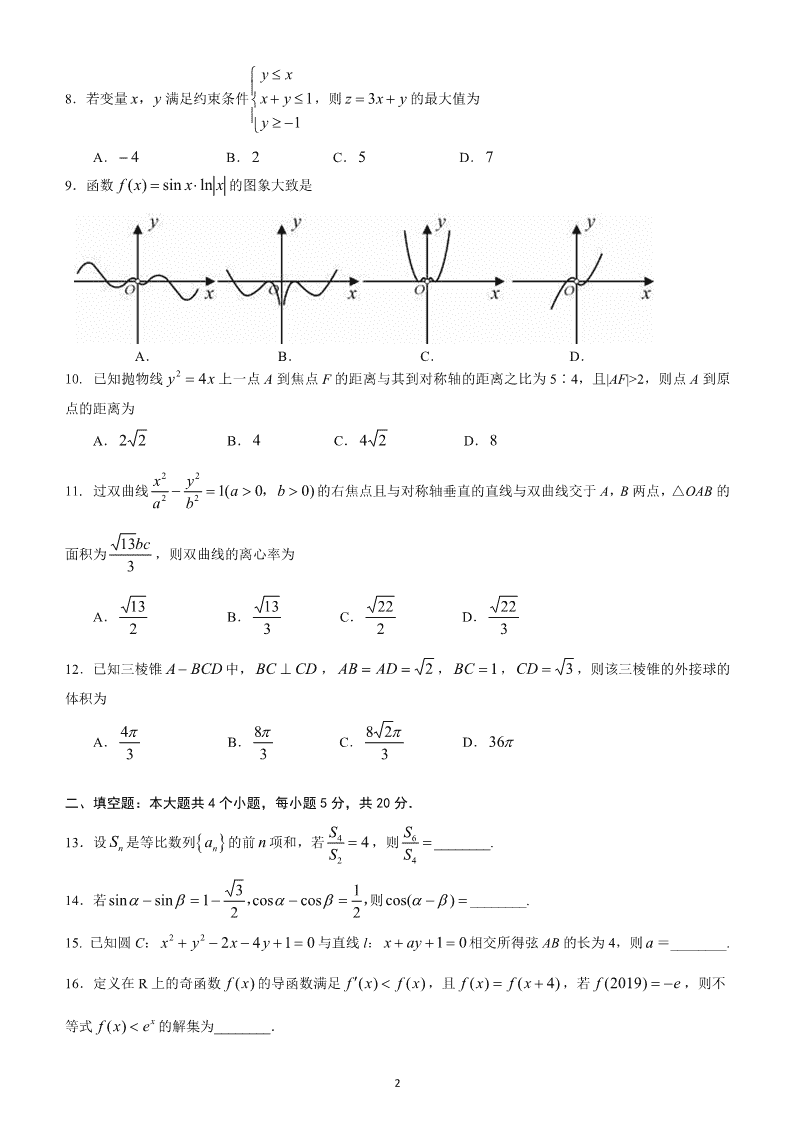
1 绝密 ★ 启用前 试卷类型 A 2016 级高三第四次模拟考试 数 学 试 卷（文科） 注意事项： 1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上． 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干 净后，再选涂其它答案标号．回答非选择题时，将答案写在答题卡上，写在本试卷上无效． 3．考试结束后，将本试卷和答题卡一并交回． 一、选择题：本大题共 12 个小题，每小题 5 分，共 60 分．每小题给出的四个选项中只有一项符合题目要求. 1．已知集合  02|  xxA ，  | 3B x x  ，则 BA A． ( 2,3) B． (0,3) C． ( 3,0) D． ( 3, 2)  2．命题 1R 2  xxx ， 的否定是 A． 1R 2  xxx ， B． 1R 2  xxx ， C． 1R 2  xxx ， D． 1R 2  xxx ， 3．在 ABC 中，O 为 AC 的中点，若 AO AB BC     ，则   A．1 B． 2 1 C． 3 2 D． 3 4 4．在等差数列 }{ na 中， 475  aa ，则数列 }{ na 的前11项和 11S A．8 B．16 C． 22 D． 44 5．若向量 a ，b 满足 3a ， 2b ，  baa  ，则 a 与 b 的夹角为 A． 6  B． 2  C． 3 2 D． 6 5 6．某四棱锥的底面为正方形，其三视图如图所示，则该四棱锥的体积为 A．1 B． 2 C．3 D． 4 7．函数      ，， ，， 1lg 11)( xx xexf x ，则 ))10(( ff A． 1101lg  B． 2 C． e D． 1e 2 8．若变量 yx， 满足约束条件 1 1 y x x y y        ，则 3z x y  的最大值为 A． 4 B． 2 C．5 D． 7 9．函数 xxxf lnsin)(  的图象大致是 A． B． C． D． 10. 已知抛物线 xy 42  上一点 A 到焦点 F 的距离与其到对称轴的距离之比为 5∶4，且|AF|>2，则点 A 到原 点的距离为 A． 22 B． 4 C． 24 D．8 11. 过双曲线 )00(12 2 2 2  bab y a x ， 的右焦点且与对称轴垂直的直线与双曲线交于 A，B 两点，△OAB 的 面积为 3 13bc ，则双曲线的离心率为 A． 2 13 B． 3 13 C． 2 22 D． 3 22 12．已知三棱锥 BCDA  中， CDBC  ， 2 ADAB ， 1BC ， 3CD ，则该三棱锥的外接球的 体积为 A． 3 4 B． 3 8 C． 3 28  D． 36 二、填空题：本大题共 4 个小题，每小题 5 分，共 20 分． 13．设 nS 是等比数列 na 的前 n 项和，若 4 2 4  S S ，则  4 6 S S ________. 14．若 ，， 2 1coscos2 31sinsin   则  )cos(  ________. 15. 已知圆 C： 014222  yxyx 与直线 l： 01  ayx 相交所得弦 AB 的长为 4，则 a ＝________. 16．定义在 R 上的奇函数 )(xf 的导函数满足 )()( xfxf  ，且 )4()(  xfxf ，若 ef )2019( ，则不 等式 xexf )( 的解集为________． 3 三、解答题（共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17-21 题为必考题，每个试题考生都必 须作答.第 22、23 题为选考题，考生根据要求作答.） （一）必考题：共 60 分. 17．（本小题满分 12 分） 已知  xxm cossin3 ， ，  xxn coscos ， ， Rx ，设 ( )f x m n   . （Ⅰ）求 )(xf 的解析式及单调递增区间； （Ⅱ）在 ABC 中，角 CBA ，， 所对的边分别为 cba ，， ，且 1a ， 2 cb ， 1)( Af ，求 ABC 的面积. 18．（本小题满分 12 分） 数列 na 的前 n 项和为 nS ，已知 1 2n n nS S a    ， 1a 2a， 5a， 成等比数列. （Ⅰ）求数列 na 的通项公式； （Ⅱ）若数列 nb 满足   na n n a b   1 2 ，求数列 nb 的前 n 项和 nT . 19．（本小题满分 12 分） 在四棱锥 ABCDP  中，底面 ABCD 是矩形， PA 平面 ABCD ， PAD 是等腰三角形， ADAB 2 ， E 是 AB 上一点，且三棱锥 BCEP  与四棱锥 ADCEP  的体积之比为 2:1 ，CE 与 DA 的延长线交于点 F ， 连接 PF . （Ⅰ）求证：平面 PCD ⊥平面 PAD ； （Ⅱ）若三棱锥 AEFP  的体积为 2 3 ，求线段 AD 的长． 20. （本小题满分 12 分） 已知函数 x xxxf 21ln)(  . （Ⅰ）求 )(xf 的单调递增区间 ； （Ⅱ）若   3 1)23( xxf ，求实数 x 的取值范围． 21．（本小题满分 12 分） 已知椭圆  012 2 2 2  bab y a x 的左、右两个焦点分别为 21 FF， ，离心率 2 2e ，短轴长为 2. （Ⅰ）求椭圆的方程； （Ⅱ）如图，点 A 为椭圆上的一动点(非长轴端点)， 2AF 的延长线与椭圆 交于 B 点， AO 的延长线与椭圆交于 C 点，求△ABC 面积的最大值． 4 （二）选考题：共 10 分.请考生在第 22、23 题中任选一题作答.如果多做，则按所做的第一题计分. 22. （本小题满分 10 分）选修 4-4：坐标系与参数方程 已知曲线C 的极坐标方程是 2  ，以极 点为原点，极轴为 x 轴的正半轴建立平面直角坐标系，直线 l 的 参数方程为 1 2 3 x t y t     （ t 为参数）. （Ⅰ）写出直线 l 的普通方程与曲线 C 的直角坐标方程； （Ⅱ）设曲线C 经过伸缩变换 ' 1' 2 x x y y   ，得到曲线 'C ，设 ( , )M x y 为曲线 'C 上任一点，求 2 23 2x xy y  的最小值，并求相应点 M 的坐标. 23. （本小题满分 10 分）选修 4-5：不等式选讲 已知实数 0a  ， 0b  ，函数 ( )f x x a x b    的最大值为 3. （Ⅰ）求 a b 的值； （Ⅱ）设函数 2( )g x x ax b    ，若对于 x a  均有 ( ) ( )g x f x ，求 a 的取值范围. 5 绝密 ★ 启用前 试卷类型 A 2016 级高三第四次模拟考试 数 学 试 卷 答 案 第Ⅰ卷（共 60 分） 一、选择题 题目 1 2 3 4 5 6 7 8 9 10 11 12 答案 A C A C A B D C A C D A 第Ⅱ卷（共 90 分） 二、填空题 13.13 4 14． 2 3 15. 1 16．  ，1 三、解答题：本大题共 6 小题，共 70 分． 17．解：（Ⅰ） xxxxf 2coscossin3)(  …………1 分 2 2cos12sin2 3 xx  2 1)62sin(  x …………3 分 令 )Z(63226222  kkxkkxk ， )(xf 的单调递增区间为 )Z(]6,3[  kkk  …………6 分 （Ⅱ）由 2 1)62sin(12 1)62sin()(   AAAf ， 又 )6 13,6(62),,0(   AA 36 5 62   AA …………8 分 )cos1(2)(cos2 2222 AbccbAbccba  …………10 分 1bc ， 4 3sin2 1   AbcS ABC …………12 分 18．解：（Ⅰ） 21  nnn aSS 211   nnnn aSSa 数列 }{ na 是公差为 2 的等差数列； …………2 分 又 521 ,, aaa 成等比数列， 2 111 2 111 )2()8()()4(  aaadadaa 6 11 a ， )(12 *Nnnan  …………5 分 （Ⅱ）由（Ⅰ）可得： nn n nnb 2)12(2)12( 2  …………6 分 nn nnn nn bbbbbT 2)12(2)32(252321 1321 1321       …………7 分 1432 2)12(2)32(2523212  nn n nnT  …………8 分 错位相减得： 132 2)12()222(22  nn n nT  …………9 分 1 1 2)12(21 )21(422     n n n 112 2)32(62)12(822   nnn nn …………10 分 62)32( 1  n n nT ………12 分 19．解：（Ⅰ）因为 PA⊥平面 ABCD，CD⊂平面 ABCD，所以 PA⊥CD. 又底面 ABCD 是矩形，所以 AD⊥CD. 因为 PA∩AD＝A，所以 CD⊥平面 PAD. 因为 CD⊂平面 PCD，所以平面 PCD⊥平面 PAD. …………6 分 （Ⅱ）不妨设 AP＝AD＝x，则 AB＝2AD＝2x，BC＝x. 因为三棱锥 PBCE 与四棱锥 PADCE 的体积之比为 1∶2， 所以 1 3×1 2BE×BC×PA 1 3×AE＋CD 2 ×AD×PA ＝1 2 ，得 BE AE＋CD ＝1 2 ，得 BE AE＋AE＋BE ＝1 2 ，得 BE＝2AE. 则 BE＝4x 3 ，AE＝2x 3 . 易知△AEF∽△BEC，则AF BC ＝AE BE ＝1 2.则 AF＝1 2x. 所以三棱锥 PAEF 的体积 V＝1 3×1 2×AF×AE×AP＝1 3×1 2×1 2x×2 3x×x＝3 2 ， 解得 x＝3，故 AD 长为 3. ………12 分 20. 解：（Ⅰ）由已知得 f(x)的定义域为(0，＋∞)． ∵f(x)＝ln x－ x 1＋2x ， ∴f′(x)＝1 x －1＋2x－2x 1＋2x2 ＝4x2＋3x＋1 x1＋2x2 . …………3 分 ∵x＞0，∴4x2＋3x＋1＞0，x(1＋2x)2＞0. ∴当 x＞0 时，f′(x)＞0. ∴f(x)在(0，＋∞)上单调递增． …………6 分 7 (2)∵f(x)＝ln x－ x 1＋2x ，∴f(1)＝ln 1－ 1 1＋2×1 ＝－1 3. 由 f[x(3x－2)]＜－1 3 得 f[x(3x－2)]＜f(1)． …………9 分 由(1)得 x3x－2＞0 x3x－2＜1 ，解得－1 3 ＜x＜0 或2 3 ＜x＜1. ∴实数 x 的取值范围为 －1 3 ，0 ∪ 2 3 ，1 . …………12 分 21．解：（Ⅰ）由题意得 2b＝2，解得 b＝1， …………1 分 ∵e＝c a ＝ 2 2 ，a2＝b2＋c2，∴a＝ 2，c＝1，故椭圆的标准方程为x2 2 ＋y2＝1 .…………4 分 （Ⅱ）①当直线 AB 的斜率不存在时，不妨取 A 1， 2 2 ， B 1，－ 2 2 ，C －1，－ 2 2 ， 故 S△ABC＝1 2 ×2× 2＝ 2； …………5 分 ②当直线 AB 的斜率存在时，设直线 AB 的方程为 y＝k(x－1)，联立方程得 y＝kx－1 x2 2 ＋y2＝1 ， 化简得(2k2＋1)x2－4k2x＋2k2－2＝0， …………6 分 设 A(x1，y1)，B(x2，y2)，x1＋x2＝ 4k2 2k2＋1 ，x1·x2＝2k2－2 2k2＋1 ， …………7 分 |AB|＝ 1＋k2·[x1＋x22－4x1·x2] ＝ 1＋k2·[ 4k2 2k2＋1 2－4·2k2－2 2k2＋1 ]＝2 2· k2＋1 2k2＋1 ， …………8 分 点 O 到直线 kx－y－k＝0 的距离 d＝ |－k| k2＋1 ＝ |k| k2＋1 ， ∵O 是线段 AC 的中点，∴点 C 到直线 AB 的距离为 2d＝ 2|k| k2＋1 ，…………9 分 ∴S△ABC＝1 2|AB|·2d＝1 2· 2 2· k2＋1 2k2＋1 · 2|k| k2＋1 ＝2 2 k2k2＋1 2k2＋12 ＝2 2 1 4 － 1 42k2＋12 ＜ 2 .…………11 分 综上，△ABC 面积的最大值为 2. …………12 分 22. 解：（Ⅰ）由 1x t  ，得 1t x  ，代入 2 3y t  ， 得直线的普通方程 3 3 2 0x y    ……2 分 由 2  ，得 2 4  ，所以 2 2 4x y  ……4 分 8 （Ⅱ）∵ ' 1' 2 x x y y   ，∴ 'C 的直角坐标方程为 2 2 14 x y  . ……6 分 ∴设  2cos ,sinM   ，则 2cos , sinx y   . ∴ 2 2 2 23 2 4cos 2 3sin cos 2sin 2cos 2 33x xy y                . ……8 分 ∴当 cos 2 13       ，即 1 3 2 x y   或 1 3 2 x y     ，上式取最小值 1. 即当 31, 2M       或 31, 2       ， 2 23 2x xy y  的最小值为 1. ……10 分 23. 解：（Ⅰ）由三角不等式 ( ) ( )x a x b x a x b a b         ， ……3 分 可得 max( ) 3f x a b   ……4 分 （Ⅱ）当 x a 时，     3f x x a x b x a x b a b             ， ……6 分 对于 x a  ，使得    g x f x 等价于  max, 3x a g x    成立， ∵  g x 的对称轴为 2 ax a   ，∴  g x 在  ,x a  为减函数， ∴  g x 的最大值为   2 2 22 3g a a a b a a        ， ……8 分 ∴ 22 3 3a a     ，即 22 0a a  ，解得 0a  或 1 2a  ， 又因为 , 0, 3a o b a b    ，所以 1 32 a  . ……10 分