- 2021-04-22 发布 |
- 37.5 KB |
- 11页
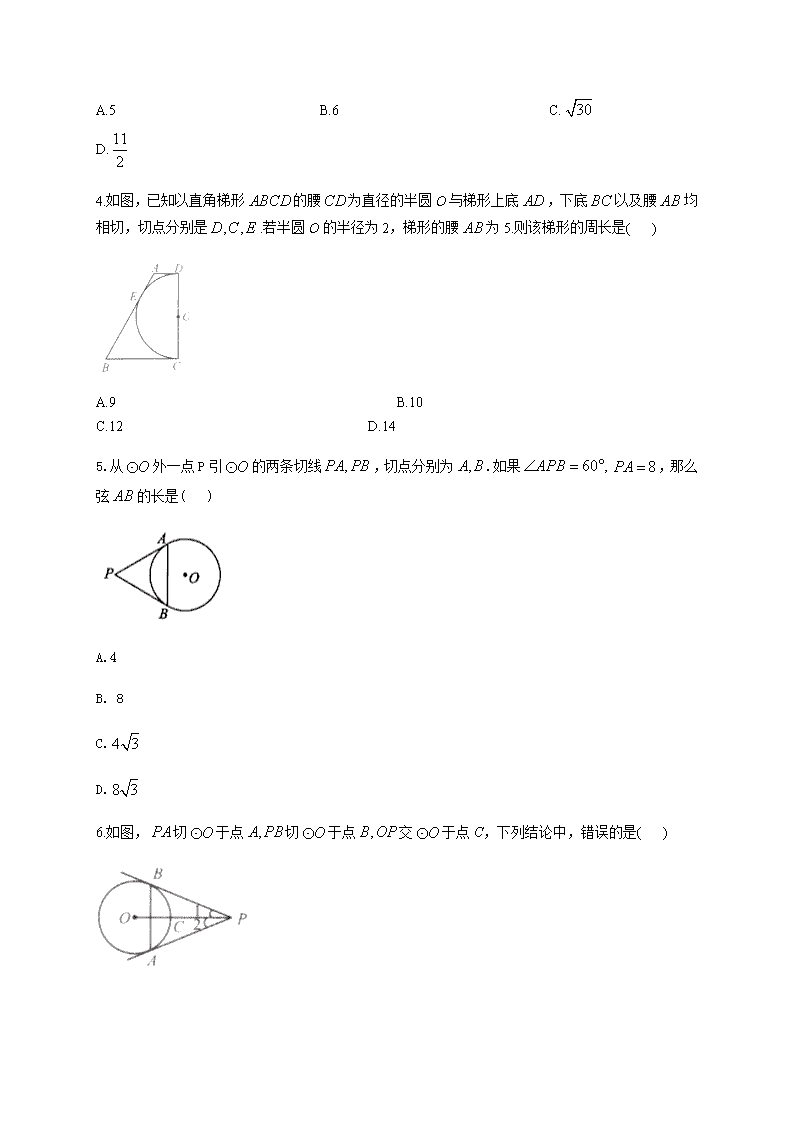
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版九年级下册数学随堂小练:3切线长定理
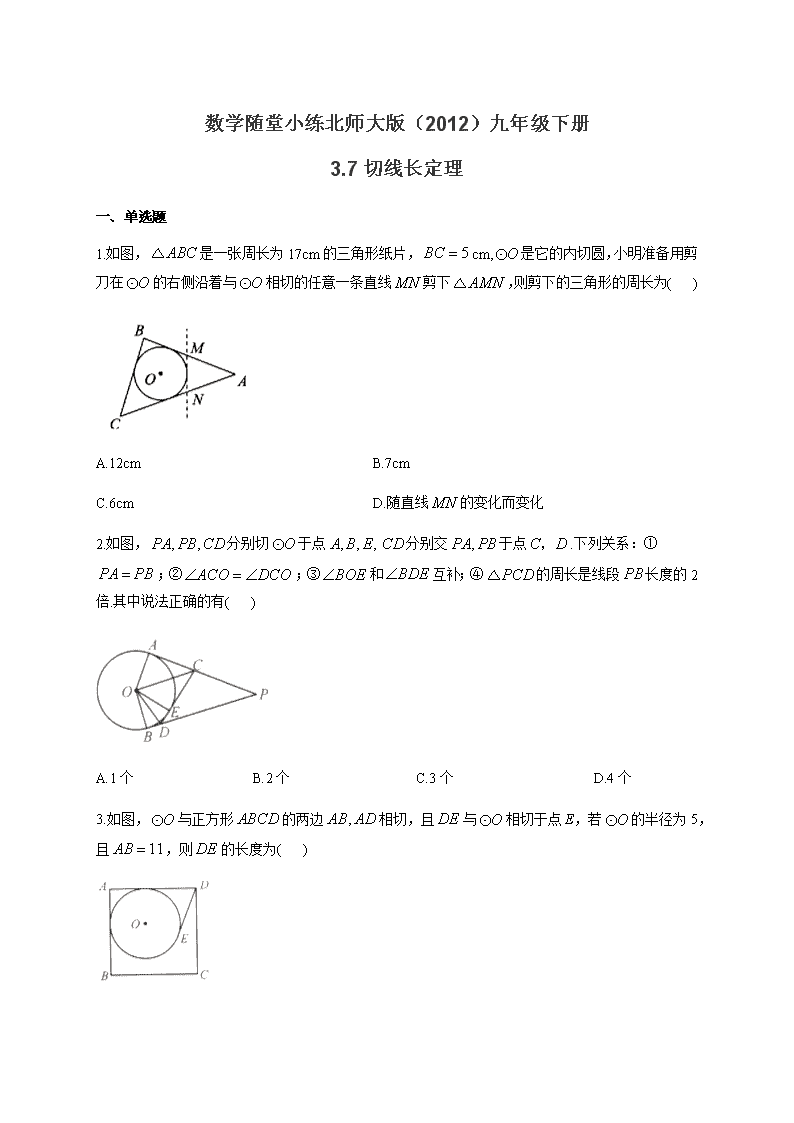
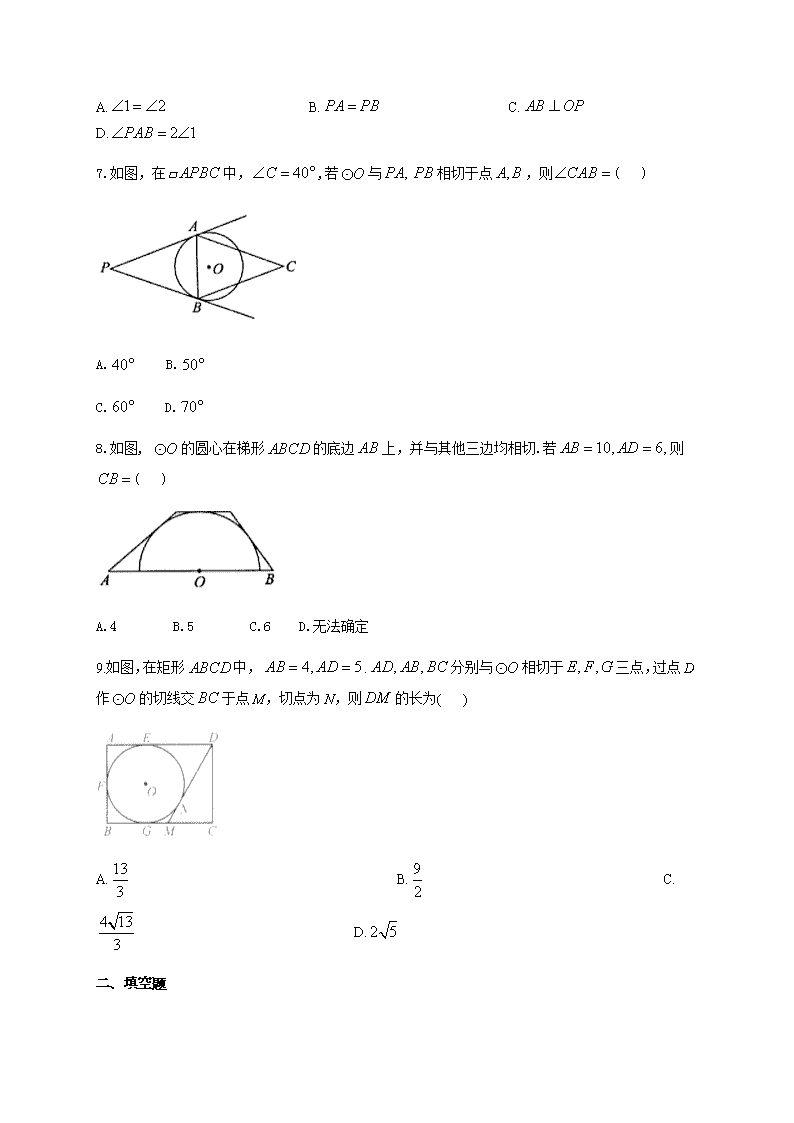
数学随堂小练北师大版(2012)九年级下册 3.7 切线长定理 一、单选题 1.如图, ABC△ 是一张周长为 17cm 的三角形纸片, 5BC cm, O 是它的内切圆,小明准备用剪 刀在 O 的右侧沿着与 O 相切的任意一条直线MN剪下 AMN△ ,则剪下的三角形的周长为 ( ) A.12cm B.7cm C.6cm D.随直线MN的变化而变化 2.如图, , ,PA PB CD分别切 O 于点 , , ,A B E CD分别交 ,PA PB于点C D, .下列关系:① PA PB ;② ACO DCO ;③ BOE 和 BDE 互补;④ PCD△ 的周长是线段 PB长度的 2 倍.其中说法正确的有( ) A.1 个 B.2 个 C.3 个 D.4 个 3.如图, O 与正方形 ABCD的两边 ,AB AD相切,且DE与 O 相切于点 E,若 O 的半径为 5, 且 11AB ,则DE的长度为( ) A.5 B.6 C. 30 D. 11 2 4.如图,已知以直角梯形 ABCD的腰CD为直径的半圆 O与梯形上底 AD,下底 BC以及腰 AB均 相切,切点分别是 , ,D C E .若半圆 O的半径为 2,梯形的腰 AB为 5.则该梯形的周长是( ) A.9 B.10 C.12 D.14 5.从 O 外一点 P 引 O 的两条切线 ,PA PB,切点分别为 ,A B .如果 60 ,APB ° 8PA ,那么 弦 AB的长是( ) A.4 B. 8 C. 4 3 D.8 3 6.如图, PA切 O 于点 ,A PB切 O 于点 ,B OP交 O 于点 C,下列结论中,错误的是( ) A. 1 2 B. PA PB C. AB OP D. 2 1PAB 7.如图,在 APBC 中, 40C °,若 O 与 , PA PB相切于点 ,A B,则 CAB ( ) A. 40° B.50° C.60° D.70° 8.如图, O 的圆心在梯形 ABCD的底边 AB上,并与其他三边均相切.若 10, 6,AB AD 则 CB ( ) A.4 B.5 C.6 D.无法确定 9.如图,在矩形 ABCD中, 4, 5AB AD . , ,AD AB BC分别与 O 相切于 , ,E F G三点,过点 D 作 O 的切线交 BC于点 M,切点为 N,则DM 的长为( ) A. 13 3 B. 9 2 C. 4 13 3 D. 2 5 二、填空题 10.在Rt ABC△ 中, 90 , 5, 12C AC BC ,则这个三角形内切圆的半径是 . 11.如图, ,PA PB切 O 于点 ,A B ,连接 AB交直线OP于点C.若 O 的半径为3, 4PA ,则OC 长为 . 12.如图, PA PB、 切 O 于点 A B、 ,已知 O 半径为 2,且 60APB ,则 AB . 13.如图,PA,PB 是⊙O 的切线,切点分别是 A,B,若 PA=6 cm,则 PB=__________. 三、解答题 14.如图,D为 O 上一点,点 C在直径 BA的延长线上,且 CDA CBD . (1)求证:CD是 O 的切线; (2)过点 B作 O 的切线交CD的延长线于点 E,若 6BC , 2 3 AD BD ,求 BE的长. 参考答案 1.答案:B 如图,设 ,E F分别是 O 的切点. ∵ ABC△ 是一张三角形纸片, 17cmAB BC AC , O 是它的内切圆,点 D是其中一个切点, 5cmBC , ∴ 5cmBD CE BC , 7cmAD AE . 易知 ,DM MF FN EN , ∴ 7cmAM AN MN AD AE .故选 B. 2.答案:D ,PA PB 是 O 的切线, ,PA PB ACO DCO ,故①②正确; ,PA PB ,CD是 O 的切线 , , 90CA CE DE DB OBD OED 360 180BOE BDE OBD OED BOE 和 BDE 互补,故③正确; PCD△ 的周长 2PC CE DE PD PC CA PD DB PA PB PA ,故④正确 故选 D. 3.答案:B 连接 ,OM ON,如图 四边形 ABCD是正方形, 11, 90AD AB A O 与正方形 ABCD的两边 AB AD、 相切 90OMA ONA , AMON 是矩形 ,OM ON AMON 是正方形 5AM OM AD 和DE与 O 相切, 11 5 6DE DM AD AM 故选 B. 4.答案:D 根据切线长定理,得 AD AE ,BC BE 所以梯形的周长是5 2 4 14 ,故选 D. 5.答案: B ,PA PB 是 O 的切线, .PA PB 60 ,APB APB △° 是等边三角形. 8, 8.PA AB 6.答案:D 由切线长定理可得: 1 2 , PA PB ,从而 AB OP 无法得出 2 1PAB ,故选 D. 7.答案:D O 与 , PA PB相切于点 , A B , PA PB . 又四边形 APBC是平行四边形.四边形 APBC是菱形. 40 , 140 ,P C PAC 1 70 2 CAB PAC ° .故选 D. 8.答案:A 如图,设 O 的半径是 R, O 与 , , AD DC CB相切于点 , , E F H , 连接 , , , , OE OD OF OC OH . 设 , CD y CB x , ABCDS S 梯形 . 则 1 1( ) ( 10) . 2 2 S CD AB R y R ① BOC COD DOAS S S S △ △ △ 1 1 1 6 2 2 2 xR yR R .② 联立①②,得 4x .即 4CB . 9.答案:A 连接 , , ,OE OF ON OG 在矩形 ABCD中, 90 , 4A B CD AB , ,AD AB BC 分别与 O 相切于 , ,E F G三点 90AEO AFO OFB BGP 四边形 ,AFOE FBGO是正方形 2AF BF AE BG , 3DE DM 是 O 的切线 3,DN DE MN MG 5 2 3CM MN MN 在Rt DMC△ 中, 2 2 2DM CD CM 2 2 2(3 ) (3 ) 4NM NM , 4 3 NM 4 133 3 3 DM ,故选 A. 10.答案:2 如图: 在Rt ABC△ , 90 , 5, 12C AC BC 根据勾股定理 2 2 13AB AC BC 四边形OECF中,OE OF , 90OEC OFC C OECF是正方形 由切线长定理.得: , ,AD AE BD BF CE CF 1 ( ) 2 CE CF AC BC AB 即 1 (5 12 13) 2 2 r 11.答案: 9 5 如图,连接 AO . ,PA PB 是 O 的两条切线, , , .OA PA PA PB APO BPO .AB OP 4, 3,AP AO 2 2 5.OP OA AP 12 . 5 OA APAC OP 2 2 9 . 5 OC OA AC 12.答案: 2 3 连接 PO AO、 , PA PB 、 是 O 的两条切线,切点分别为 A B、 , PA PB 60APB , PAB△ 是等边三角形 PA PB 、 切 O 于点 A B、 , 30APO 在直角 APO△ 中, 2 2 3 tan 30 3 3 OAAP 2 3AB AP , 故答案为 2 3 13.答案:6 cm 14.答案:(1)证明:连结OD, ∵OB OD ,∴ OBD BDO , ∵ CDA CBD ,∴ CDA ODB , 又 AB是 O 的直径,∵ 90 90ADO ODB ADO CDA , 即 90CDO ,∴CD是 O 的切线; (2)解:∵ C C CDA CBD , , ∴ CAD CDB△ △ ,∴ 2 3 CD AD BC BD , ∵ 6BC ,∴ 4CD ∵CE BE、 是 O 的切线, ∴ BE DE BE BC , , ∴ 2 2 2BE BC EC 即 2 2 2(4 ) 6BE BE , 解得 5 2 BE 查看更多