江苏省无锡市普通高中2020届高三上学期期末调研考试数学试题 含解析

江苏省无锡市普通高中2020届高三上学期期末调研考试数学试题 含解析

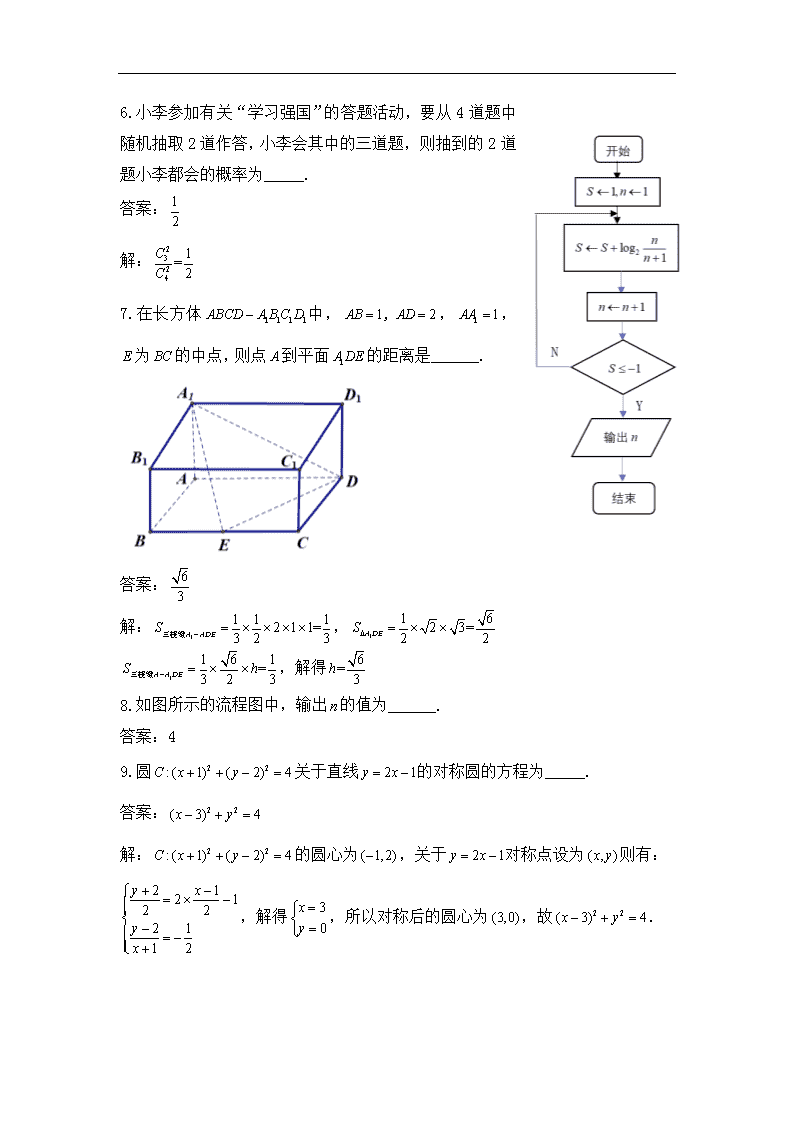
无锡市普通高中2019年秋学期高三期终调研考试卷 ‎ 数学 2020.1‎ 注意事项及说明：本卷考试时间为120分钟，全卷满分160分.‎ 一、填空题：本大题共14小题，每小题5分，共70分.不需要写出解答过程，请把答案直接填写在答题卡相应位置上.‎ ‎1.集合，，则_____.‎ 答案：‎ 解：因为表示为奇数，故 ‎2.已知复数，且满足（其中为虚数单位），则____.‎ 答案：-8‎ 解：，所以，所以 ‎3.某校高二（4）班统计全班同学中午在食堂用餐时间，有7人用时为6分钟，有14人用时7分钟，有15人用时为8分钟，还有4人用时为10分钟，则高二（4）班全体同学用餐平均用时为____分钟.‎ 答案：7.5 ‎ 解：‎ ‎4.函数过定点________.‎ 答案： ‎ 解：由指数函数的性质，可得过定点 ‎5.等差数列（公差不为0），其中，，成等比数列，则这个等比数列的公比为_____.‎ 答案：4‎ 解：设等差数列的公差为，由题意得: ，则 整理得，，所以 ‎6.小李参加有关“学习强国”的答题活动，要从4道题中随机抽取2道作答，小李会其中的三道题，则抽到的2道题小李都会的概率为_____.‎ 答案：‎ 解：‎ ‎7.在长方体中，,，，为的中点，则点到平面的距离是______.‎ 答案：‎ 解：，‎ ‎，解得 ‎8.如图所示的流程图中，输出的值为______.‎ 答案：4‎ ‎9.圆关于直线的对称圆的方程为_____.‎ 答案：‎ 解：的圆心为，关于对称点设为则有：‎ ‎，解得，所以对称后的圆心为，故.‎ ‎10.正方形的边长为2，圆内切与正方形，为圆的一条动直径，点为正方形边界上任一点，则的取值范围是______.‎ 答案：‎ ‎11.双曲线的左右顶点为，以为直径作圆，为双曲线右支上不同于顶点的任一点，连接角圆于点，设直线的斜率分别为，若，则_____.‎ 答案：‎ ‎12.对于任意的正数，不等式恒成立，则的最大值为_____.‎ 答案：‎ ‎13.在直角三角形中，为直角，，点在线段上，且,若，则的正切值为_____.‎ 答案：3 ‎ ‎14.函数在区间内有且仅有两个零点，则实数的取值范围是_____.‎ 二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤 ‎15. （本小题满分14分）‎ 在中，角所对的分别为，向量，向量，且.‎ ‎（1）求角的大小；‎ ‎（2）求的最大值.‎ ‎16. （本小题满分14分）‎ 在四棱锥中，底面是平行四边形，为其中心，为锐角三角形，且平面底面，为的中点，.‎ ‎（1）求证：平面；‎ ‎（2）求证：.‎ ‎17. （本小题满分14分）‎ 已知椭圆的左右焦点分别为，焦距为4，且椭圆过点，过点且不行与坐标轴的直线交椭圆与两点，点关于轴的对称点为，直线交轴于点.‎ ‎（1）求的周长；‎ ‎（2）求面积的最大值.‎ ‎18. （本小题满分16分）‎ 一酒企为扩大生产规模，决定新建一个底面为长方形MNPQ的室内发酵馆，发酵馆内有一个无盖长方体发酵池，其底面为长方形ABCD(如图所示) ,其中AD≥AB.结合现有的生产规模，设定修建的发酵池容积为450米3,深2米.若池底和池壁每平方米的造价分别为200元和150元，发酵池造价总费用不超过65400元 (1) 求发酵池AD边长的范围;‎ ‎(2)在建发酵馆时，发酵池的四周要分别留出两条宽为4米和米的走道(为常数).问:发酵池的边长如何设计，可使得发酵馆古地面积最小.‎ ‎19.（本小题满分16分）‎ 已知，均为正项数列，其前项和分别为，，且，，，当，时，，.‎ ‎（1）求数列，的通项公式；‎ ‎（2）设，求数列的前项和.‎ ‎20.（本小题满分16分）‎ 设函数，，.‎ ‎（1）求函数的单调区间；‎ ‎（2）若函数有两个零点，（）.‎ ‎（Ⅰ）求的取值范围；‎ ‎（Ⅱ）求证：随着的增大而增大.‎ 附加题，共40分 ‎21．【选做题】本题包括A，B两小题，每小题10分，共计20分，解答时应写出文字说明，证明过程或演算步骤．‎ A．选修4—2：矩阵与变换 已知a，b，矩阵A＝，若矩阵A属于特征值5的一个特征向量为，点P(﹣2，1)在A对应的变换作用下得到点P′(﹣1，2)，求矩阵A．‎ B．选修4—4：坐标系与参数方程 已知曲线C1：，（其中为参数），以坐标原点O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为，设曲线C1与曲线C2交于A，B两点，求AB的长．‎ ‎【必做题】第22题、第23题，每题10分，共计20分，解答时应写出文字说明，证明过程或演算步骤．‎ ‎22．（本小题满分10分）‎ 如图，矩形ABCD所在的平面垂直于平面AEB，O为AB的中点, ∠AEB＝90°，‎ ‎∠EAB＝30°，AB＝，AD＝3．‎ ‎（1）求异面直线OC与DE所成角的余弦值；‎ ‎（2）求二面角A—DE—C的正弦值．‎ ‎23．（本小题满分10分）‎ 对于任意的x＞1，，用数学归纳法证明：．‎