名校领航高考数学预测试卷

名校领航高考数学预测试卷

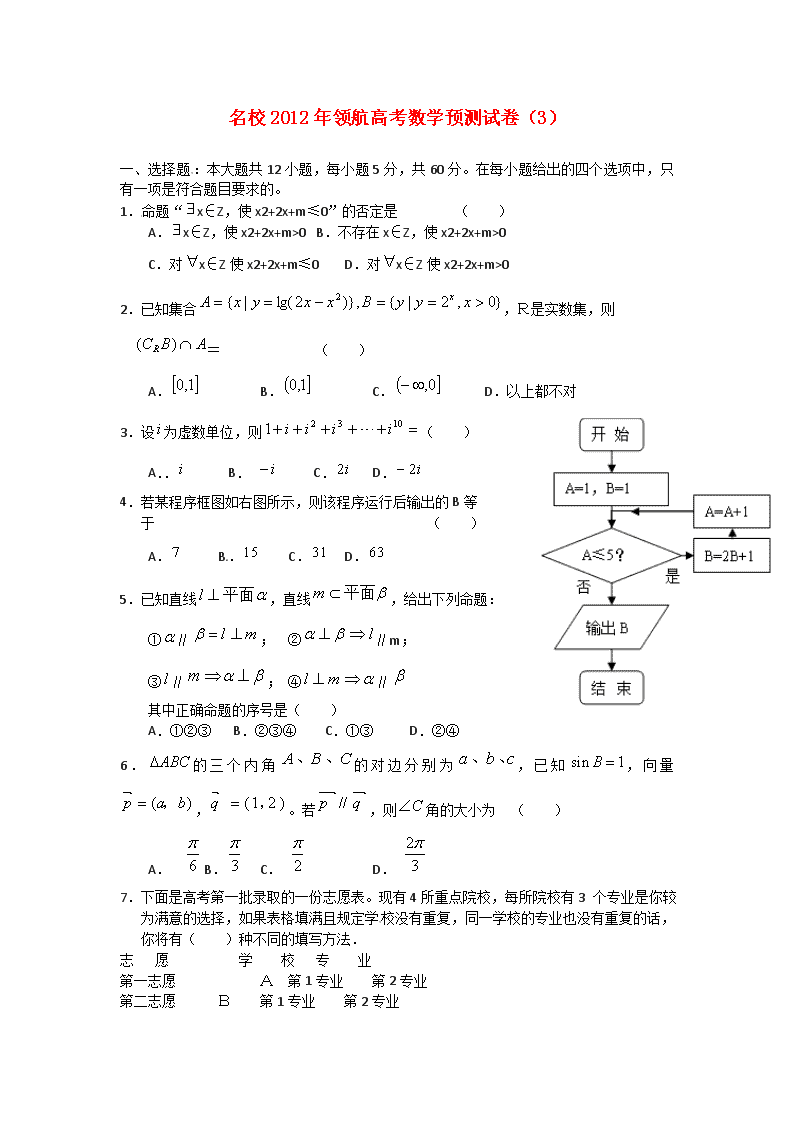
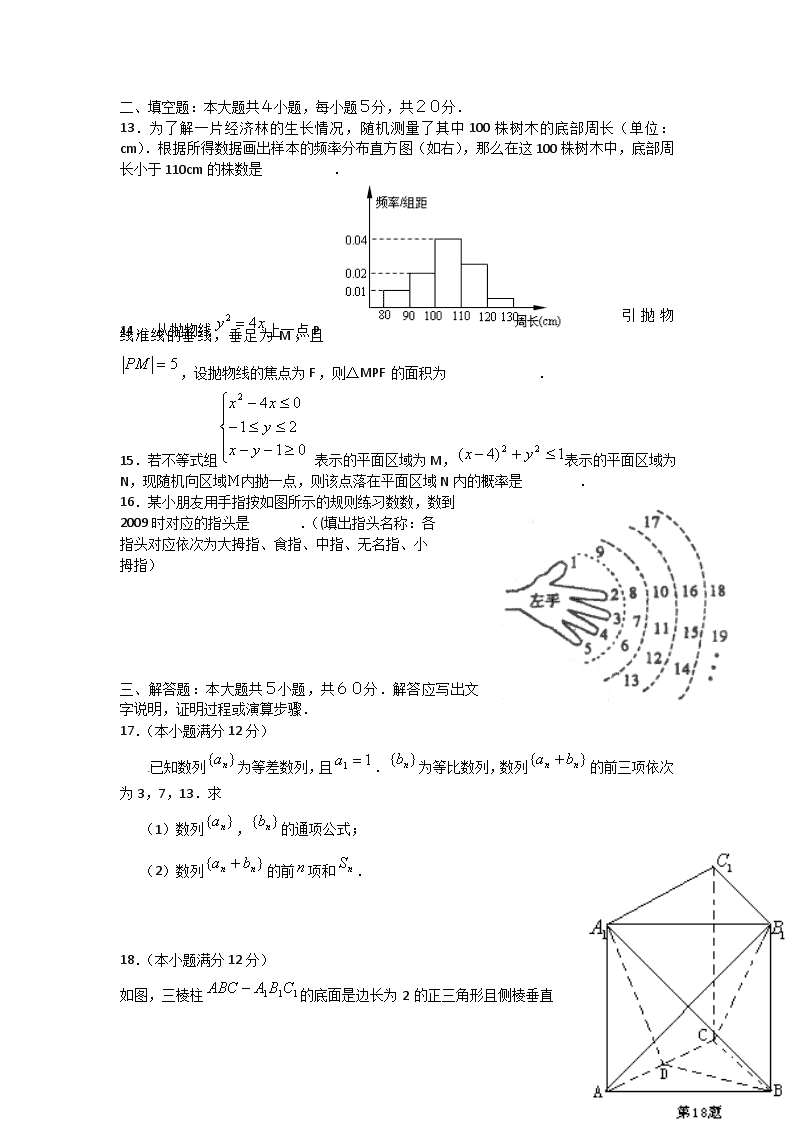
名校2012年领航高考数学预测试卷（3）‎ 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．命题“x∈Z，使x2+2x+m≤0”的否定是 （　　）‎ ‎ A．x∈Z，使x2+2x+m>0 B．不存在x∈Z，使x2+2x+m>0‎ ‎ C．对x∈Z使x2+2x+m≤0 D．对x∈Z使x2+2x+m>0‎ ‎2．已知集合，Ｒ是实数集，则 ‎ ＝ （　　）‎ ‎ A．　　 B．　　　 C．　　 D．以上都不对 ‎3．设为虚数单位，则（ 　）‎ ‎ A．． B． C． D． ‎ ‎4．若某程序框图如右图所示，则该程序运行后输出的B等 ‎ 于 （ ）‎ ‎ A． B． C． D．‎ ‎5．已知直线，直线，给出下列命题：‎ ‎ ①∥； ②∥m；‎ ‎ ③∥； ④∥‎ ‎ 其中正确命题的序号是（ ）‎ ‎ A．①②③ B．②③④ C．①③ D．②④‎ ‎6．的三个内角的对边分别为，已知，向量， 。若，则角的大小为 （　　）‎ ‎ A． B． C． 　　　　 D． ‎ ‎7．下面是高考第一批录取的一份志愿表。现有4所重点院校，每所院校有3 个专业是你较 ‎ 为满意的选择，如果表格填满且规定学校没有重复，同一学校的专业也没有重复的话，‎ ‎ 你将有（ ）种不同的填写方法．‎ 志 愿 学 校 专 业 ‎ 第一志愿 Ａ 第1专业 第2专业 第二志愿 Ｂ 第1专业 第2专业 第三志愿 Ｃ 第1专业 第2专业 ‎ A． B． C． D．‎ ‎8．一个几何体按比例绘制的三视图如图所示（单位：m） （ ）‎ ‎ 则该几何体的体积为（ 　　）．‎ ‎ A． B． C． D．‎ ‎9．函数的图象与x轴所围成的封闭图形的面积为 （ ）‎ ‎ A． B． 1 C． 2 D．‎ ‎10．若多项式，则 （　　）‎ ‎ A．9 B．10 C．-9 D．-10‎ ‎11．已知双曲线，直线交双曲线于Ａ、B两点，的面积为S（O为原点），则函数的奇偶性为 （　 ）‎ ‎ A．奇函数 B．偶函数 ‎ C．不是奇函数也不是偶函数 D．奇偶性与、有关 ‎12．定义一种运算，令，且，则函数的最大值是 （ 　 ）‎ ‎ A． B．1 C． D．‎ 二、填空题：本大题共４小题，每小题５分，共２０分．‎ ‎13．为了解一片经济林的生长情况，随机测量了其中100株树木的底部周长（单位：cm）．根据所得数据画出样本的频率分布直方图（如右），那么在这100株树木中，底部周长小于110cm的株数是 ．‎ ‎14． 从抛物线上一点P引抛物线准线的垂线，垂足为M，且，设抛物线的焦点为F，则△MPF的面积为 ．‎ ‎15．若不等式组 表示的平面区域为M，表示的平面区域为N，现随机向区域Ｍ内抛一点，则该点落在平面区域N内的概率是 ．‎ ‎16．某小朋友用手指按如图所示的规则练习数数，数到 ‎2009时对应的指头是 ．（(填出指头名称：各 指头对应依次为大拇指、食指、中指、无名指、小 拇指）‎ 三、解答题：本大题共５小题，共６０分．解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（本小题满分12分）‎ ‎ 已知数列为等差数列，且．为等比数列，数列的前三项依次为3，7，13．求 ‎ （1）数列，的通项公式；‎ ‎ （2）数列的前项和．‎ ‎18．（本小题满分12分）‎ 如图，三棱柱的底面是边长为2‎ 的正三角形且侧棱垂直于底面，侧棱长是，D是AC的中点。‎ ‎ （1）求证：平面；‎ ‎ （2）求二面角的大小；‎ ‎ （3）求直线与平面所成的角的正弦值．‎ ‎19．（本小题满分12分）‎ ‎ 在一次食品卫生大检查中，执法人员从抽样中得知，目前投放我市的甲、乙两种食品的合格率分别为和．‎ ‎ （1）今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率．‎ ‎ （2）若某消费者从两种食品中任意各购一件,设表示购得不合格食品的件数,试写出 的分布列,并求其数学期望．‎ ‎20．（本小题满分l2分）‎ 设椭圆的焦点分别为、，直线：交轴于点，且．‎ ‎ （1）试求椭圆的方程；‎ ‎ （2）过、分别作互相垂直的两直线与椭圆分别交于、、、四点（如图所示），试求四边形面积的最大值和最小值．‎ ‎ ‎ ‎21． (本小题满分l2分)‎ ‎ 已知函数．‎ ‎ （1）求的导数；‎ ‎ （2）求证：不等式上恒成立；‎ ‎ （3）求的最大值．‎ 四、选考题（本题满分10分，请从所给的三道题中任选一题做答，并在答题卡上填写所选题目的题号，如果多做，则按所做的第一题记分．）‎ ‎22．（本小题满分10分）‎ ‎ 如图，是⊙的一条切线，切点为，都是⊙的割线，已知 ‎．‎ ‎ （1）证明：；‎ ‎ （2）证明：．‎ ‎23．（本小题满分10分）‎ ‎ 已知曲线的参数方程为（为参数），曲线的极坐标方程为．‎ ‎ （1）将曲线的参数方程化为普通方程，将曲线的极坐标方程化为直角坐标方程；‎ ‎ （2）曲线，是否相交，若相交请求出公共弦的长，若不相交，请说明理由．‎ ‎24．（1）已知关于的不等式在上恒成立，求实数的最小值；‎ ‎ （2）已知，求证：．‎ 参考答案 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ 题号 ‎ ‎１‎ ‎２‎ ‎３‎ ‎４‎ ‎５‎ ‎６‎ ‎７‎ ‎８‎ ‎９‎ ‎１０‎ ‎１１‎ ‎１２‎ 答案 D B A D Ｃ B D Ｃ A D Ｂ A ‎1．答案：Ｄ ‎2．答案：Ｂ　由 ‎ 由，‎ ‎ 则，‎ ‎3．答案：Ａ　　由．另该题也可直接用的周期 ‎ 性解答．‎ ‎4．答案：Ｄ ‎5．答案：Ｃ 由垂直、平行可得． ‎ ‎6．答案：Ｂ 由，‎ ‎ ∥，‎ ‎ 故 ‎7．答案：Ｄ ‎8．答案：Ｃ　所以：‎ ‎ ‎ ‎9．答案：Ｄ　‎ ‎10．答案：Ｄ　，‎ ‎ 题中 ‎ 故 ‎11．答案：B ‎ ‎ 注意到双曲线的对称性可知： ‎ ‎ 所以．‎ ‎12．答案：Ａ　由于 ‎ ‎ ‎ ，‎ ‎ ‎ 二、填空题：本大题共４小题，每小题５分，共２０分．‎ ‎13．答案：70由图可知：底部周长小于110cm的株树为：‎ ‎14．答案：１０　准线x=-1，,‎ ‎ ‎ ‎15．答案：　如图所示：‎ ‎ ‎ ‎16．答案：从第二行起，周期为８得对应的指头是大拇指．‎ 三、解答题：本大题共５小题，共６０分．解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（本题１２分） 解：①设公差为，公比为 ‎ ‎ ‎ 　…………………………………(６分)‎ ‎ ②‎ ‎ ‎ ‎　　…………………………………(1２分)‎ ‎18．（本题１２分）‎ ‎ 解法一：（1）设与相交于点P，连接PD，则P为中点，‎ D为AC中点，PD//。‎ ‎ 又PD平面D，‎ ‎ //平面D ……………………(４分)‎ ‎ （2）正三棱住，‎ ‎ 底面ABC。‎ ‎ 又BDAC ‎ BD ‎ 就是二面角的平面角。‎ ‎ =，AD=AC=1‎ ‎ tan =‎ ‎ =, 即二面角的大小是 …………………(８分)‎ ‎ （3）由（2）作AM，M为垂足。‎ ‎ BDAC，平面平面ABC，平面平面ABC=AC ‎ BD平面，‎ ‎ AM平面，‎ ‎ BDAM ‎ BD = D ‎ AM平面，连接MP，则就是直线与平面D所成的角。‎ ‎ =，AD=1，在RtD中，=， ‎ ‎ ，。‎ ‎ ‎ ‎ 直线与平面D所成的角的正弦值为…………………(1２分)‎ ‎ 解法二：‎ ‎ （1）同解法一 ‎ （2）如图建立空间直角坐标系，‎ ‎ 则D（0，0，0），A（1，0，0），（1，0，），B（0，，0），（0，，）‎ ‎=（-1，，-），=（-1，0，-）‎ 设平面的法向量为n=（x，y，z）‎ ‎ 则n ‎ n ‎ 则有，得n=（，0，1）‎ ‎ 由题意，知=（0，0，）是平面 ‎ ABD的一个法向量。‎ ‎ 设n与所成角为，‎ ‎ 则，‎ ‎ ‎ ‎ 二面角的大小是 ‎ （3）由已知，得=（-1，，），n=（，0，1）‎ ‎ 则 ‎ 直线与平面D所成的角的正弦值为 ‎19．（本题１２分）‎ ‎ （1）‎ ‎ 因为每人从两种食品中各取一件，两件恰好都是不合格食品的概率为0．02，所以三人分别从中各取一件，恰好有一人取到两件都是不合格品的事件，可看做三次独立重复试验问题。‎ ‎ …………………………………(６分)‎ ‎ （2）‎ ‎ ‎ ‎ ‎ ‎ 所求的分布列为：‎ ‎0‎ ‎1‎ ‎2‎ P ‎0.72‎ ‎0.26‎ ‎0.02‎ ‎ E=…………………………(１２分)‎ ‎20．（本题12分）‎ ‎ 解：（1）由题意，‎ ‎ 为的中点　　　　‎ ‎ ‎ ‎ 即：椭圆方程为…………………(５分)‎ ‎ （2）方法一：当直线与轴垂直时，，此时，四边形的面积．同理当与轴垂直时，也有四边形的面积． 当直线，均与轴不垂直时，设:，代入消去得： 设所以，， 所以，，同理所以四边形的面积 令因为当 ‎，且S是以u为自变量的增函数，所以．‎ ‎ 综上可知，．故四边形面积的最大值为4，最小值为．…（12分）‎ ‎ 方法二：用直线的参数方程中的几何意义．‎ ‎21．（本题12分）‎ ‎ 解：（1）………………………………………(2分)‎ ‎（2）由（1）知，其中 ‎ 令，对求导数得 ‎ ‎ ‎ = 在上恒成立．‎ ‎ 故即的导函数在上为增函数，故 ‎ 进而知在上为增函数，故 ‎ 当时，显然成立．‎ ‎ 于是有在上恒成立．…………………………（９分）‎ ‎ （3） 由（2）可知在上恒成立．‎ ‎ 则在上恒成立．即在单增 ‎ 于是……………………（12分）‎ ‎22．（本题10分）证明：（1） ‎ ‎ ‎ ‎ 又 ‎ ‎ ……………………（5分）‎ ‎ （2） 由（1）有 ‎ 又 ‎ ‎ ‎ ‎ ‎ 又 ‎ ‎ ‎ ‎ …………………………………（１０分）‎ ‎23．（本题10分）解：（1）由得 ‎ ‎ ‎ ∴曲线的普通方程为 ‎ ∵‎ ‎ ∴‎ ‎ ∵‎ ‎ ∴，即 ‎ ∴曲线的直角坐标方程为 ‎ …………………………………（５分）‎ ‎ （2）∵圆的圆心为，圆的圆心为 ‎ ∴‎ ‎ ∴两圆相交 ‎ 设相交弦长为，因为两圆半径相等，所以公共弦平分线段 ‎ ∴‎ ‎ ∴‎ ‎ ∴公共弦长为……………………（10分）‎ ‎24．（本题１0分）解：‎ ‎ （1），‎ ‎ …………………（5分）‎ ‎ （2）因为……（10分） ‎