- 2021-04-22 发布 |
- 37.5 KB |
- 11页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江省温州市2020—2021学年八年级上学期期末测试卷B卷(附答案)
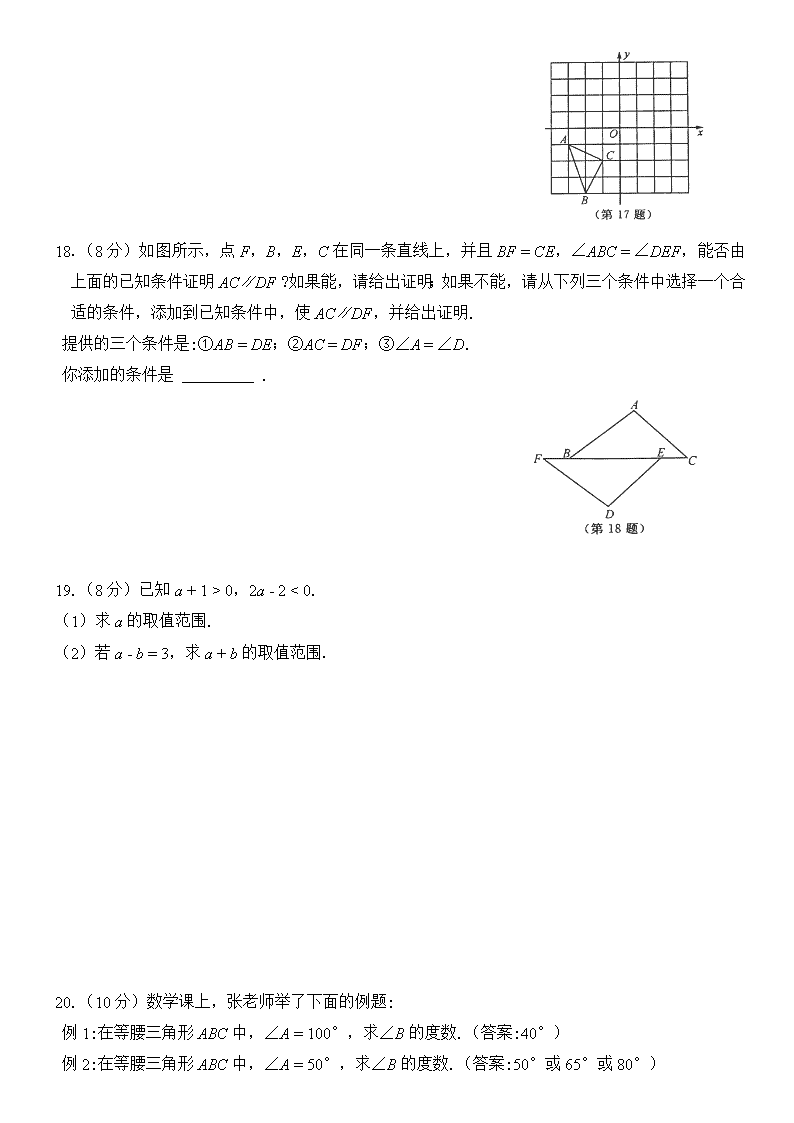
2020 学年浙江省温州市八年级上学期期末测试卷 B 卷 姓名 班级 学号___________ 一、选择题(每题 3 分,共 30 分) 1.已知 a < 0,则下列不等式中,不成立的是( ) A.2a < a B.a2 > 0 C.1 - 2a < 1 D.a - 2 < 0 2.若一个三角形的两边长分别为 4 和 8,则第三边长可以是( ) A.4 B.12 C.13 D.10 3.下列语句中,属于命题的是( ) A.对顶角相等吗 B.作∠BAC 的平分线 AD C.两个锐角的和大于 90° D.在线段 AB 上取一点 C 4.如图所示,一艘海轮位于灯塔 P 的南偏东 70°方向的 M 处,它以每小时 40 海里的速度向正北方 向航行,2h 后到达位于灯塔 P 的北偏东 40°的 N 处,则 N 处与灯塔 P 的距离为( ) A.40 海里 B.60 海里 C.70 海里 D.80 海里 5.已知下列命题:①若|a| = |b|,则 a2 = b2;②若 am2 > bm2,则 a > b;③对顶角相等;④等腰三角 形的两底角相等.其中原命题和逆命题均为真命题的个数是( ) A.1 B.2 C.3 D.4 6.在平面直角坐标系中,点 M,N,P,Q 的位置如图所示.若直线 y = kx 经过第一、三象限,则直 线 y = kx - 2 可能经过的点是( ) A.点 M B.点 N C.点 P D.点 Q 7.如图所示,在△ABC 中,∠ACB = 90°,分别以点 A,B 为圆心,大于 1 2 AB 长为半径画弧,两弧 交于点 M,N,作直线 MN 分别交 AB,AC 于点 D,E,连结 CD,BE.下列结论中,错误的是( ) A.AD = CD B.BE > CD C.∠BEC = ∠BDC D.BE 平分∠CBD 8.如图所示,在△ABC 中,∠ABC,∠ACB 的平分线交于点 O,D 是∠ACB 外角平分线与∠ABC 平 分线交点,E 是∠ABC,∠ACB 外角平分线交点.若∠BOC = 120°,则∠D 的度数为( ) A.15° B.20° C.25° D.30° 9.若关于 x 的不等式组 axx xx 4 23 ,1)3(32 有四个整数解,则 a 的取值范围是( ) A. - 11 4 < a≤ - 5 2 B. - 11 4 ≤a < - 5 2 C. - 11 4 ≤a≤ - 5 2 D. - 11 4 < a < - 5 2 10.如图所示,在 Rt△ABC 中,∠BAC = 90°,AB = 6,AC = 8,将边 AB 沿 AE 翻折,使点 B 落在 BC 上的点 D 处,再将边 AC 沿 AF 翻折,使点 C 落在 AD 延长线上的点 C′处,两条折痕与斜边 BC 分别交于点 E,F,则线段 C′F 的长为( ) A. 8 5 B. 2 3 C. 3 5 D. 4 5 二、填空题(每题 4 分,共 24 分) 11.在△ABC 中,已知∠A = 100°,∠B = 60°,则∠C = _________ . 12.已知点 P1(a,7),P2(a + 1,9)在直线 y = kx + 7 上,则 k = _________ . 13.如图所示,在△ABC 中,∠C = 90°,边 AB 的垂直平分线分别交 AB, AC 边于点 D,E,连结 BE.若 AB = 10,BC = 6,则△BCE 的周长是 _________ . 14.游泳池的水质要求三次检验的 pH 的平均值不小于 7.2,且不大于 7.8,前两次检验,pH 的读数 分别为 7.4 和 7.9,要使水质合格,则第三次检验的 pH 的读数 x 的取值范围是 _________ . 15.等腰三角形一腰长为 5,一边上的高线长为 3,则底边长为 _________ . 16.在△ABC 中,∠C = 90°,AC = 8 cm,BC = 6 cm.动点 P 从点 C 开始按 C→A→B→BC 的路径绕 △ABC 的边运动一周,速度为 2 cm/s,运动的时间为 t(s).当△BCP 为等腰三角形时,t 的值是 _________ . 三、解答题(共 66 分) 17.(6 分)在如图所示的平面直角坐标系中,每个小方格都是边长为 1 的正方形,△ABC 的顶点均 在格点上. (1)将△ABC 沿 y 轴正方向平移 3 个单位得到△A1B1C1,画出△A1B1C1,并写出点△B1 的坐标. (2)画出△A1B1C1 关于 y 轴对称的△A2B2C2,并写出点△C2 的坐标. 18.(8 分)如图所示,点 F,B,E,C 在同一条直线上,并且 BF = CE,∠ABC = ∠DEF,能否由 上面的已知条件证明 AC∥DF ?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合 适的条件,添加到已知条件中,使 AC∥DF,并给出证明. 提供的三个条件是:①AB = DE;②AC = DF;③∠A = ∠D. 你添加的条件是 _________ . 19.(8 分)已知 a + 1 > 0,2a - 2 < 0. (1)求 a 的取值范围. (2)若 a - b = 3,求 a + b 的取值范围. 20.(10 分)数学课上,张老师举了下面的例题: 例 1:在等腰三角形 ABC 中,∠A = 100°,求∠B 的度数.(答案:40°) 例 2:在等腰三角形 ABC 中,∠A = 50°,求∠B 的度数.(答案:50°或 65°或 80°) 张老师启发同学们进行变式,小敏编了如下一题: 变式:在等腰三角形 ABC 中,∠A = 70°,求∠B 的度数. (1)请你解答小敏编的变式题. (2)解答(1)后小敏发现,∠A 的度数不同得到∠B 的度数的个数也可能不同.如果在等腰三角形 ABC 中,设∠A = x°,当∠B 有三个不同的度数时,请你探索 x 的取值范围. 21.(10 分)现从 A,B 两个水果市场向甲、乙两地运送水果,A,B 两个水果市场各有水果 20 t, 其中甲地需要水果 22 t,乙地需要水果 18 t,从 A 水果市场到甲地运费为 50 元/t,到乙地为 30 元 /t;从 B 水果市场到甲地运费为 60 元/t,到乙地为 45 元/t. (1)设 A 水果市场运送 x(t)水果到甲地,请完成下表: (2)设总运费为 y 元,请写出 y 关于 x 的函数表达式,求出自变量 x 的取值范围,并在平面直角 坐标系中画出此函数的图象. (3)当 A,B 两个水果市场向甲、乙两地运送水果各多少吨时,总运费最少?最少是多少? 22.(12 分)“五一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票. 经调查发现,在车站开始检票时,有 640 人排队检票,检票开始后,仍有旅客继续前来排队检票 进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队 检票进站 16 人,每分钟每个检票口检票 14 人.已知检票的前 a(min)只开放了两个检票口.某一 天候车室排队等候检票的人数 y(人)与检票时间 x(min)的关系如图所示. (1)求 a 的值. (2)求检票到第 20min 时,候车室排队等候检票的旅客人数. (3)若要在开始检票后 15 min 内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检, 则检票一开始至少需要同时开放几个检票口? 23.(12 分)已知△ABC 是等边三角形,D 是 BC 边上的一动点,连结 AD. (1)如图 1 所示,若 BD = 2,DC = 4,求 AD 的长. (2)如图 2 所示,以 AD 为边作∠ADE = ∠ADF = 60°,分别交 AB,AC 于点 E,F. ①小明通过观察、实验,提出猜想:在点 D 运动的过程中,始终有 AE = AF,小明把这个猜想与同 学们进行交流,通过讨论,形成了证明该猜想的两种想法. 想法 1:利用 AD 是∠EDF 的平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形 的相关知识获证. 想法 2:利用 AD 是∠EDF 的平分线,构造△ADF 的全等三角形,然后通过等腰三角形的相关知识 获证 请你参考上面的想法,帮助小明证明 AE = AF(一种方法即可). ②小聪在小明的基础上继续进行思考,发现:四边形 AEDF 的面积与 AD 的长存在一定的关系.若用 S 表示四边形 AEDF 的面积,x 表示 AD 的长,请你直接写出 S 与 x 之间的函数表达式.查看更多