- 2021-04-21 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2010年崇文区中考二模数学试题
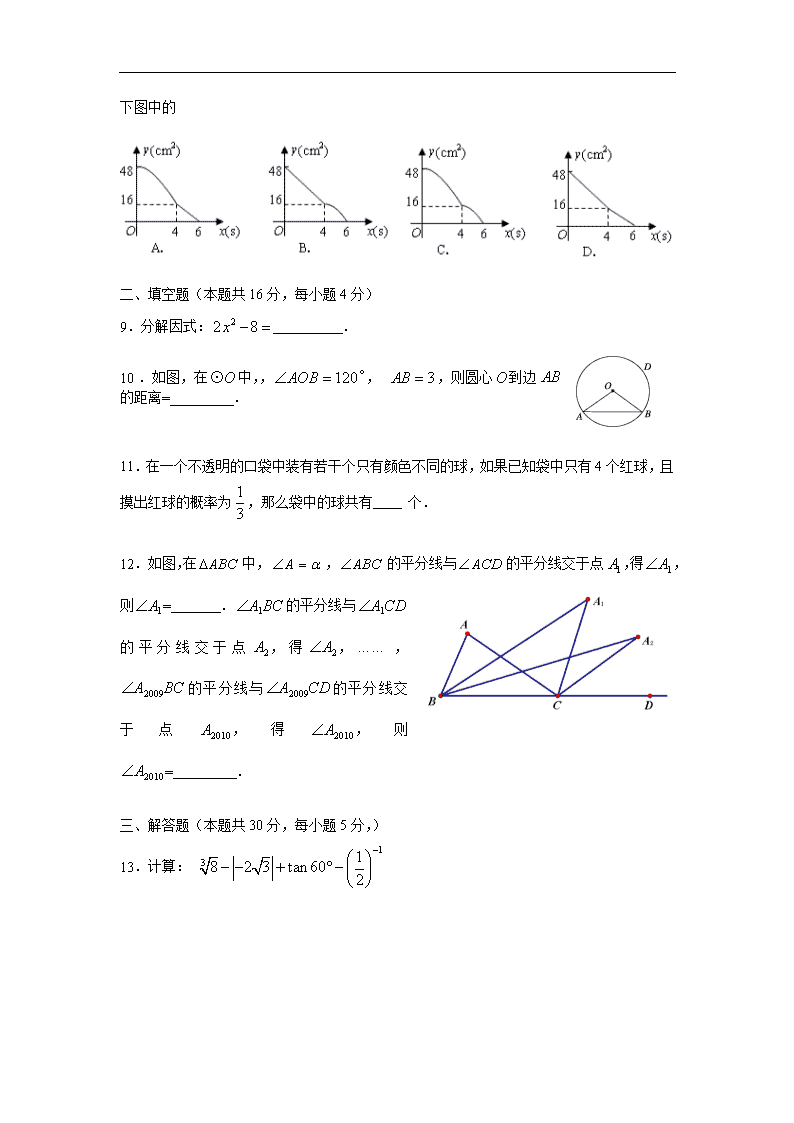
崇文区2009—2010学年度第二学期初三统一练习(二) 数 学 试 卷 2010.6 一、选择题(本题共32分,每小题4分) 1. 计算的结果是 A. B. C. D. 2.近似数所表示的准确值的范围是 A.<≤ B. ≤< C.<≤ D. ≤< 3. 抛物线的顶点是 A.(1,2) B.(,2) C.(1,) D.(,) 4.下列说法正确的是 A.6的平方根是 B.对角线相等的四边形是矩形 C.近似数0.270有3个有效数字 D.两个底角相等的梯形一定是等腰梯形 5.一组数据的方差为9,将这组数据中的每个数据都扩大到原来的2倍,得到一组新数据的方差是 A.9 B.18 C.36 D.81 6.一个正方体的表面展开图如图所示,每一个面上都写有一个整数, 并且相对两个面上所写的两个整数之和都相等,那么 A.a=1,b=5 B.a=5,b=1 C.a=11,b=5 D.a=5,b=11 7. 某人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离S(米)与时间t(秒)间的关系式为S=10t+t2,若滑到坡底的时间为2秒,则此人下滑的高度为 A.24米 B.12米 C.米 D.11米 8.矩形ABCD中,.动点E从点C开始沿边CB向点以2cm/s的速度运动至点B停止,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:),则y与x 之间的函数关系用图象表示大致是下图中的 二、填空题(本题共16分,每小题4分) 9.分解因式: . 10.如图,在中,,, ,则圆心到边的距离= . 11.在一个不透明的口袋中装有若干个只有颜色不同的球,如果已知袋中只有4个红球,且摸出红球的概率为,那么袋中的球共有 个. 12. 如图,在中,,的平分线与的平分线交于点,得,则= .的平分线与的平分线交于点,得,……,的平分线与的平分线交于点,得,则= . 三、解答题(本题共30分,每小题5分,) 13.计算: 14.解不等式组: D C A B E F 15.如图,是平行四边形对角线上两点,,求证:. 16.已知,求的值. 17.如图,点的坐标为,过点作轴的平行线交轴于点,作交双曲线()于点,连结.已知.求的值和直线的解析式. 18.要对一块长60米、宽40米的矩形荒地进行绿化和硬化.设计方案如图所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形面积的,求P、Q两块绿地周围的硬化路面的宽. 四、解答题(本题共20分,第19题5分,第20题5分,第21题6分,第22题4分) 19.如图,在梯形ABCD中,AB∥CD,BD⊥AD,BC=CD,∠A=60°,CD=2cm. (1)求cos∠CBD的值; (2)求梯形ABCD的面积. 20.如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点 E. (1) 求∠AEC的度数; (2)求证:四边形OBEC是菱形. 21.为推进阳光体育活动的开展,某校九年级三班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与,各活动小组人数分布情况的扇形图和条形图如下: (1)求该班学生人数; (2)请你补上条形图的空缺部分; (3)求跳绳人数所占扇形圆心角的大小. 22.如图,将矩形沿图中虚线(其中)剪成①②③④四块图形,用这四块图形恰能拼成一个正方形. (1)画出拼成的正方形的简图; (2)的值等于 . 五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.已知一元二次方程的一根为 2. (1)求关于的函数关系式; (2)求证:抛物线与轴有两个交点; (3)设抛物线与x轴交于A、B两点(A、B不重合),且以AB为直径的圆正好经过该抛物线的顶点.求的值. 24.如图,在平面直角坐标系中,是坐标原点,点A、B的坐标分别为和,连接. (1)现将绕点按逆时针方向旋转90°,得到,(点A落到点C处),请画出,并求经过、、三点的抛物线对应的函数关系式; (2)将(1)中抛物线向右平移两个单位,点的对应点为点,平移后的抛物线与原抛物线相交于点.为平移后的抛物线对称轴上一个动点,连结,当取得最大值时,求点P的坐标; (3)在(2)的条件下,当点在抛物线对称轴上运动时,是否存在点使为直角三角形?如果存在,请求出点的坐标;如果不存在,请说明理由. 25.在梯形中,∥,,且.对角线相交于点,等腰直角三角板的直角顶点落在梯形的顶点上,使三角板绕点旋转。 (1)如图1,当三角板旋转到点落在边上时,线段与的位置关系是 ,数量关系是 ; (2)继续旋转三角板,旋转角为.请你在图2中画出图形,并判断(1)中结论还成立吗?如果成立请加以证明;如果不成立,请说明理由; (3)如图3,当三角板的一边与梯形对角线重合时,与相交于点P,若,求的长。 图1 图2 图3 崇文区2009—2010学年度第二学期初三统一练习(二) 数学试卷参考答案 2010.6 一、选择题(本题共32分,每小题4分) 题号 1 2 3 4 5 6 7 8 答案 C D D C C A B A 二、填空题(本题共16分,每小题4分) 题号 9 10 11 12 答案 12 , 三、解答题(本题共30分,每小题5分,) 13.解: = = 14.解:解不等式①得 . 解不等式②得 . 所以, 原不等式组的解集是. 15.证明:平行四边形中,,, .又,. D C A B E F 在和中 , . 16.解: = =. ,,. 原式=. 17.解:(1)点的坐标为,,. 的坐标是(0,). 在把中,. 坐标是(2,). 点在双曲线上,. 、两点在函数的图象上, 解得 直线的解析式为. 18.解:设两块绿地周围的硬化路面的宽都为米,根据题意,得: 解之,得: 经检验,不符合题意,舍去. 答:两块绿地周围的硬化路面宽都为10米. 四、解答题(本题共20分,第19题5分,第20题5分,第21题6分,第22题4分) 19.解:(1)∵∠A=60°,BD⊥AD,∴∠ABD=30° 又∵AB∥CD,∴∠CDB=∠ABD=30° ∵BC=CD,∴∠CBD=∠CDB=30° cos∠CBD=. (2)过作于点. ∵∠ABD=∠CBD=30°,∴∠ABC=60°=∠A ∴AD=BC=CD=2cm 在Rt△ABD中,AB=2AD=4cm.= ==. 20.(1)解:在△AOC中,AC=2, ∵ AO=OC=2, ∴ △AOC是等边三角形.∴ ∠AOC=60°, ∴∠AEC=30°. (2)证明:∵OC⊥l,BD⊥l. ∴ OC∥BD. ∴ ∠ABD=∠AOC=60°. ∵ AB为⊙O的直径, ∴ △AEB为直角三角形,∠EAB=30°. ∴∠EAB=∠AEC. ∴ 四边形OBEC 为平行四边形. 又∵ OB=OC=2. ∴ 四边形OBEC是菱形. 解:(1)由扇形图可知,乒乓球小组人数占全班人数的. 由条形图可知,乒乓球小组人数为12. 故全班人数为. (2)由扇形图可知,篮球小组人数为. 由条形图可知,足球小组人数为16. 人数 16 12 8 足球 篮球 乒乓球 跳绳 项目 故跳绳小组人数为. 所以各小组人数分布情况的条形图为 (3)因为跳绳小组人数占全班人数的, 所以,它所占扇形圆心角的大小为. 22.解:(1)如右图 (2) 五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.(1)解:由题意,得,即. (2)证明:∵一元二次方程的判别式, 由(1)得, ∴一元二次方程有两个不相等的实根. ∴抛物线与轴有两个交点. (3)解:由题意,. 解此方程得 的顶点坐标是。 以AB为直径的圆经过顶点, 。 解得, 24.解:(1) ① 若 则解得 ② 若 则解得 ① 若 则解得 综上所述,存在点使为直角三角形,,, 25.解: (1) 垂直,相等 (2) 画图如右图(答案不唯一) (1)中结论仍成立。 证明如下: 过A作于M, 则四边形ABCM为矩形. ∴AM=BC=2,MC=AB=1. ∵tan∠ADC=2, ∴. ∴DC=BC. (3)∥ ∽ 同理可求得 由(2)知, 又 ∽查看更多