湖北省恩施市2020-2021学年八年级上期期末监测数学试题（含答案）

湖北省恩施市2020-2021学年八年级上期期末监测数学试题（含答案）

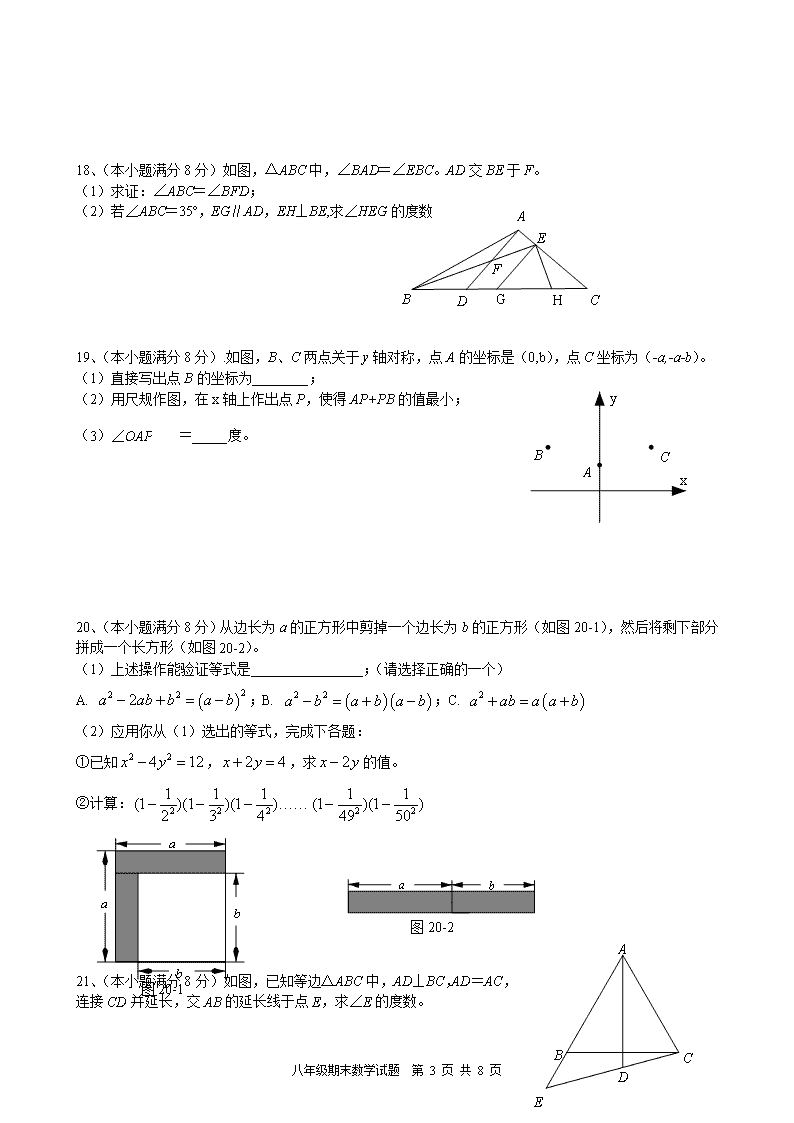
八年级期末数学试题 第 1 页 共 8 页 恩施市 2020-2021学年八年级上期期末监测 数学试题卷 本试卷共 6页，24个小题，满分 120分，考试用时 120分钟 一、选择题(本大题共有 12 个小题，每小题 3分，共 36分．在每小题给出的四个选项中，只有一项是符 合题目要求的，请将正确选择项前的字母代号填涂在答题卷相应位置．．．．．．．上) 1、计算  23xy 的结果是 A. 6xy B. 2 3x y C. 2 6x y D. 2 5x y 2、下列说法正确的是 A.形状相同的两个三角形全等 B.面积相等的两个三角形全等 C.完全重合的两个三角形全等 D.所有的等边三角形全等 3、计算： 201920202021 5.1) 3 2()1(  的结果 A. 2 3  B. 2 3 C. 3 2 D. 3 2  4、为了维修某高速公路需开凿一条长为 1300米的隧道，为了提高工作效率，高速公路建设指挥部决定由 甲、乙两个工程队从两端同时开工。已知甲工程队比乙工程队每天能多开凿 10 米，且甲工程队开凿 300 米所用的天数与乙工程队开凿 200米所用的天数相同，则甲、乙两个工程队每天各能开凿 A.20米、30米 B. 30米、20米 C. 40米、30米 D. 20米、50米 5、把      2 1 1 2, , 1 2 3 3x x x x    通分过程中，不正确的是 A.最简公分母是    22 3x x  B.       2 2 31 2 2 3 x x x x      C.        2 1 3 2 3 2 3 x x x x x       D.      2 2 2 2 4 3 2 3 x x x x      6、将一张正方形纸片按图 1、图 2方式折叠，然后用剪刀沿图 3中虚线剪掉一角，再将纸片展开铺平后得 到图形是 7、已知△ABC的六个元素，甲、乙、丙三个三角形中标出了某些元素，则与△ABC全等的三角形是 A.只有乙 B.只有丙 C.甲和乙 D.乙和丙 甲 乙 丙7题图 6题图 图 1 图 2 图 3 A B C D 八年级期末数学试题 第 2 页 共 8 页 8、如图，在四边形 ABCD中，且点 F，E分别在边 AB，BC上，将△BFE 沿 FE翻折，得到△GFE，若 GF∥AD，GE∥DC，则∠B的度数为 A.95º B.100º C.105º D.110º 9、如图，AE∥BD，∠1＝120º，∠2＝40º，则∠C的度数是 A.15º B. 20º C.25º D.30º 10、如图，在△ABC中，∠BAC＝90º，AB＝AC，AD经过 A点的一条射线，且 B、C在 AD的两侧，BD⊥AD 于 D，CE⊥AD于 E，交 AB于点 F，CE＝10，BD＝4，则 DE的长为 A.8 B.6 C.5 D.4 11、如图，△ABC是等边三角形，点 D为 AC边上一点，以 BD为边作等边△BDE，连接 CE。若 CD＝1， CE＝3，则 BC长为 A.4 B.4.5 C.3 D.3.5 12、在一个凸 n边形的纸板上切下一个三角形后，剩下的一个内角和为 1080º的多边形，则 n的值为 A.7 B. 8 C.9 D.以上都有可能 二、填空题：（本大题共 4小题，每小题 3分，计 12分，不要求写解答过程，请把答案直接写在答题卷相． 应的位置．．．．上） 13、已知  1 1,5P a  和  2 2, 1P b  关于 x轴对称，则 2020)( ba  的值为____▲____。 14、关于 x的方程 2 1 1 a a x    无解，则 a的值是____▲____。 15、2016年 2月 6日凌晨，宝岛高雄发生 6.7级地震，得知消息后，中国派出武警部队探测队，探测队探 测出某建筑物下面有生命迹象，他们在生命迹象上方建筑物的一侧地面上的 A，B两处，用仪器探测生命 迹象 C，已知探测线与地面的夹角分别是 30º和 60º（如图），则∠C的度数是____▲____。 16、已知 2 3 4 3 5 6 3 2 5 4 3 6 5 4 33, 10, 15 1 2 1 2 3 1 2 3 4 C C C                  ，… 观察以上计算过程，寻找规律计算： 5 8C  ____▲____。 三、解答题（本大题共 8 小题，满分 72分．解答应写出文字说明、证 明过程或演算步骤．） 17、（本小题满分 12分，其中（1），（2），（3）题各 4分） ⑴解方程： 2 1 3 4 4 1 2 1 4 2 x x x x       ⑵因式分解：    3 26 9 9x y x y x y     15题图 9题图 10题图 8题图 11题图 八年级期末数学试题 第 3 页 共 8 页 ⑶先化简，再求值： 23 4 41 1 1 x xx x x         ，其中 1x  。 18、（本小题满分 8分）如图，△ABC中，∠BAD＝∠EBC。AD交 BE于 F。 （1）求证：∠ABC＝∠BFD； （2）若∠ABC＝35º，EG∥AD，EH⊥BE,求∠HEG的度数 19、（本小题满分 8分）.如图，B、C两点关于 y轴对称，点 A的坐标是（0,b），点 C坐标为（-a,-a-b）。 （1）直接写出点 B的坐标为________； （2）用尺规作图，在 x轴上作出点 P，使得 AP+PB的值最小； （3）∠OAP ＝_____度。 20、（本小题满分 8分）从边长为 a的正方形中剪掉一个边长为 b的正方形（如图 20-1），然后将剩下部分 拼成一个长方形（如图 20-2）。 （1）上述操作能验证等式是________________；（请选择正确的一个） A.  22 22a ab b a b    ；B.    2 2a b a b a b    ；C.  2a ab a a b   （2）应用你从（1）选出的等式，完成下各题： ①已知 2 24 12x y  ， 2 4x y  ，求 2x y 的值。 ②计算： ) 50 11)( 49 11() 4 11)( 3 11)( 2 11( 22222  H 图 20-1 图 20-2 八年级期末数学试题 第 4 页 共 8 页 21、（本小题满分 8分）如图，已知等边△ABC中，AD⊥BC，AD＝AC，连接 CD并延长，交 AB的延长 线于点 E，求∠E的度数。 22、（本小题满分 8分）甲、乙两超市分别用 3000元以相同的进价购进质量相同的苹果，甲超市的销售方 案是：将苹果按大小分类包装销售销售，其中大苹果 400千克，以进价的 2倍价格销售，剩下的小苹果以 高于进价 10%销售。乙超市的销售方案是：不将苹果按大小分类，直接包装销售价格价格按甲超市按大、 小两种苹果售价的平均数定价，若两超市将苹果全部售完，其中甲超市获利 2100元（其它不计成本）。问： （1）苹果进价为每千克多少元？ （2）乙超市获利多少元？并比较哪种销售方式更合算。 23、（本小题满分 10 分）如图，△ABC中，∠BAC＝90º，AB＝AC，AD⊥BC于 D，AE平分∠BAD，交 BC于点 E。在△ABC外有一点 F，FA⊥AE，FC⊥BC。 （1）求证：BE＝CF； （2）在 AB上取一点 P，使 BP＝2DE，连接 PC，交 AD于点 N，连接 PE。 求证：PE⊥BC 八年级期末数学试题 第 5 页 共 8 页 24、（本题 10分）如图 24-1，直线 AB与 x轴负半轴，y轴的正半轴分别交于 A、B，OA、OB的长分别为 a、b，且满足 2 22 0a ab b   。 （1）判断△AOB的形状； （2）如图 24-2，过坐标原点作直线OQ交直线AB于第三象限的点Q，过A、B两点分别作AM⊥OQ，BN⊥OQ， 垂足分别为 M、N。若 AM＝7，BN＝4，求 MN的长； （3）如图 24-3，E为 AB上一动点，以 AE为斜边作等腰直角三角形 ADE，P为 BE的中点，延长 DP至 F， 使 PF＝DP，连接 PO、BF。试问 DF、PO是否存在确定的位置关系和数量关系？写出你的结论并证明。 图 24-2图 24-1 图 24-3 八年级期末数学试题 第 6 页 共 8 页 恩施市 2020年秋季学期八年级期末监测 数学试题参考答案 一、选择题(本大题共有 12 个小题，每小题 3 分，共 36 分．在每小题给出的四个选项中，只有一项是符 合题目要求的，请将正确选择项前的字母代号填涂在答题卷相应位置．．．．．．．上) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C C A B A B D A B B A D 二、填空题：（本大题共 4 小题，每小题 3 分，计 12 分，不要求写解答过程，请把答案直接写在答题卷相． 应的位置．．．．上） 13、1； 14、a=0,1； 15.∠C=30º； 16、 5 8C  56； 三、解答题（本大题共 8 小题，满分 72 分．解答应写出文字说明、证明过程或演算步骤．） 17、（本小题满分 12 分，其中（1），（2），（3）题各 4 分） ⑴ 6x  ；………………………4 分 ⑵   2[( ) 3]x y x y   ；………………………4分 ⑶ 2 2 x x    =3；………………………4分(注：化简正确得 3分，求值 1分) 18、（1）略；………………………4分 （2）∠HEG＝55º………………………4 分 19、（1）（a,-a-b）；………………………2 分 （2）略；………………………3分 （3）∠OAP＝45º；………………………3分 20、（1）B；………………………2 分 （2）① 2x y =3；………………………3分 ② 1 51 51 2 50 100   ………………………3 分 21、∠E=45º；………………………8分 22、（1）设苹果进价为每千克 x元，根据题意得： 3000400 10%( 400) 2100x x x    解得 x=5 经检验，x=5 是原分式方程的解 八年级期末数学试题 第 7 页 共 8 页 即苹果进价每千克 5 元。………………………4分 （2）由（1）得，每个超市苹果的总量为 3000 5 =600（千克） 大、小苹果售价分别为 10 元和 5．5元， 乙超市： 10 5.5600 ( 5) 1650 2     （元） 因为甲超市获利 2100 元，所以甲超市销售方式更合算；………………………4分 23、（1） ABE ACF   （ASA） BE＝CF；………………………5分 （2）过点 E 作 EH⊥AB 于 H，则△BEH 是等腰直角三角形， ∴HE=BH，∠BEH=45°， ∵AE 平分∠BAD，AD⊥BC， ∴DE=HE，∴DE=BH=HE， ∵BP=2DE，∴HE=HP ， ∴△HEP 是等腰直角三角形， ∴∠MEH=45°，∴∠BEP=45°+45°=90°， ∴PE⊥BC；………………………5 分 24、（1）△AOB 为等腰直角三角形；………………………3 分 （2）∵AM⊥OQ，BN⊥OQ， ∴∠AMO=∠ONB=90°， 又∵∠AOB=90°， ∴∠AOM+∠BON=90°， 又∵∠MAO+∠MOA=90°， ∴∠MAO=∠BON，在△AMO 和△ONB 中 MAO BON AMO ONB AO BO             ∴△AMO≌△ONB（AAS）， ∴ON=AM=7，OM=BN=4， 八年级期末数学试题 第 8 页 共 8 页 ∴MN=ON-OM=7-4=3；………………………3 分 （3） 1 2 OP DF 且 OP⊥DF，证明：连接 OD，OF， ∵P为 BE 的中点， ∴BP=EP， 在△BPF 和△EPD 中 BP EP BPF EPD PF PD           ∴△BPF≌△EPD（SAS） ∴BF=ED，∠FBP=∠DEP， 又∵△AED 是等腰直角三角形， ∴AD=ED，∠DEA=∠DAE=45°， ∴BF=AD，∴∠FBP=∠DEP=180°-45°=135°， 又∵△AOB 和△ADE 是等腰直角三角形， ∴OB=OA，∠DEA=∠DAE=45°，∴BF=AD， ∴∠FBO=∠FBP-∠ABO=135°-45°=90°，∠DAO=∠DAE+∠BAO=45°+45°=90°， ∴∠FBO=∠DAO=90°，在△FBO 和△DAO 中 BO AO FBO DAO BF AD           ∴△FBO≌△DAO（SAS） ∴∠FOB=∠DOA，OD=OF，∴∠DOF=∠DOB+∠BOF=∠DOB+∠DOA=∠AOB=90°， ∴△DOF 是等腰直角三角形， 又∵PF=DP， ∴ 1 2 OP DF ，OP⊥DF．………………………4 分