2012年江西中考数学试卷

2012年江西中考数学试卷

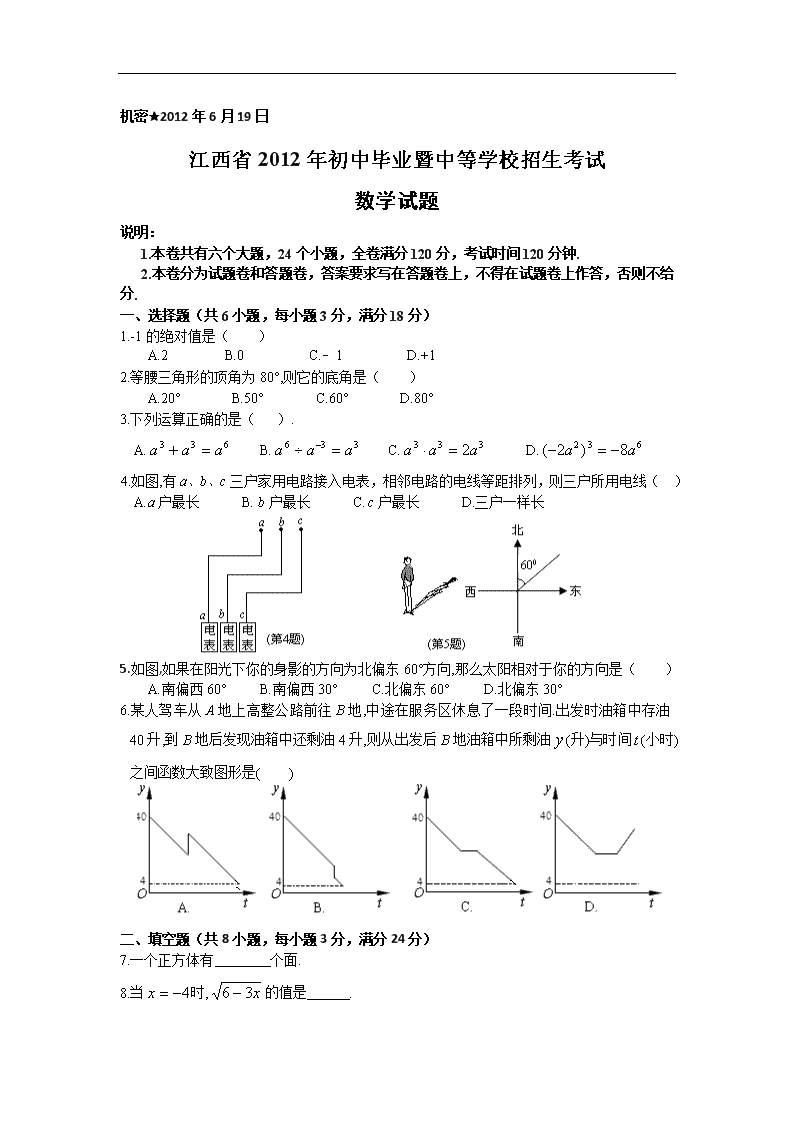
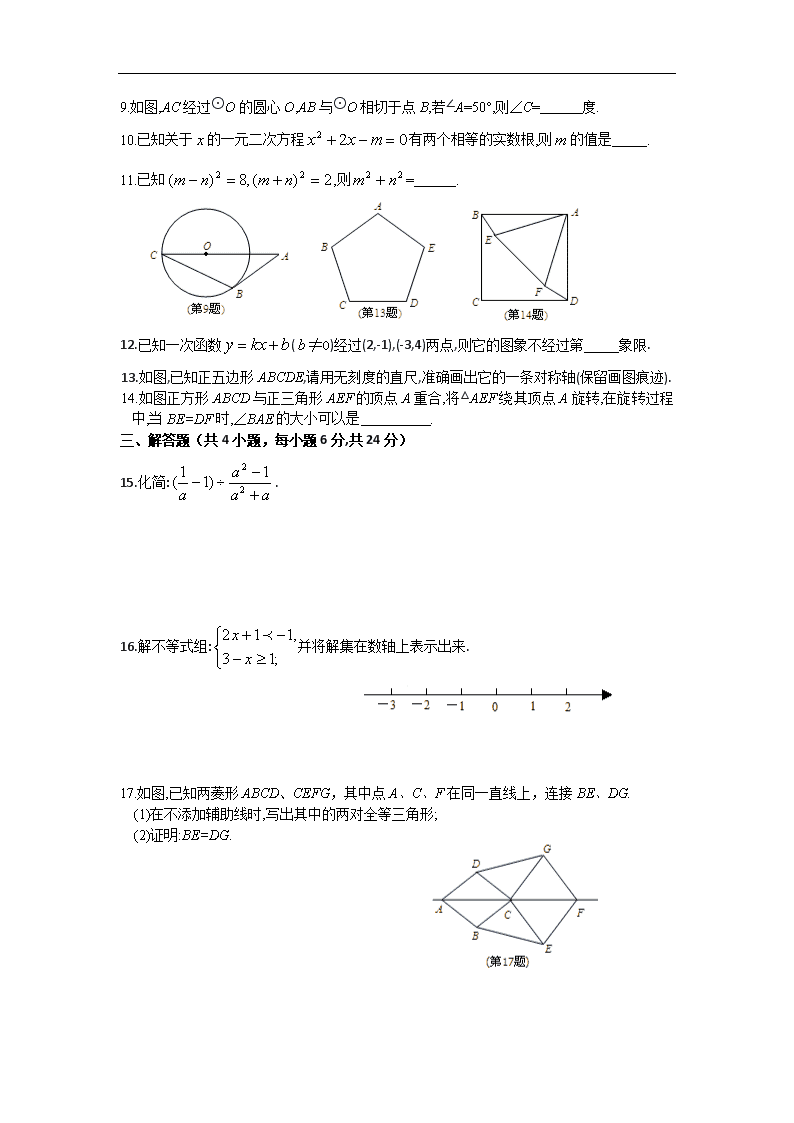
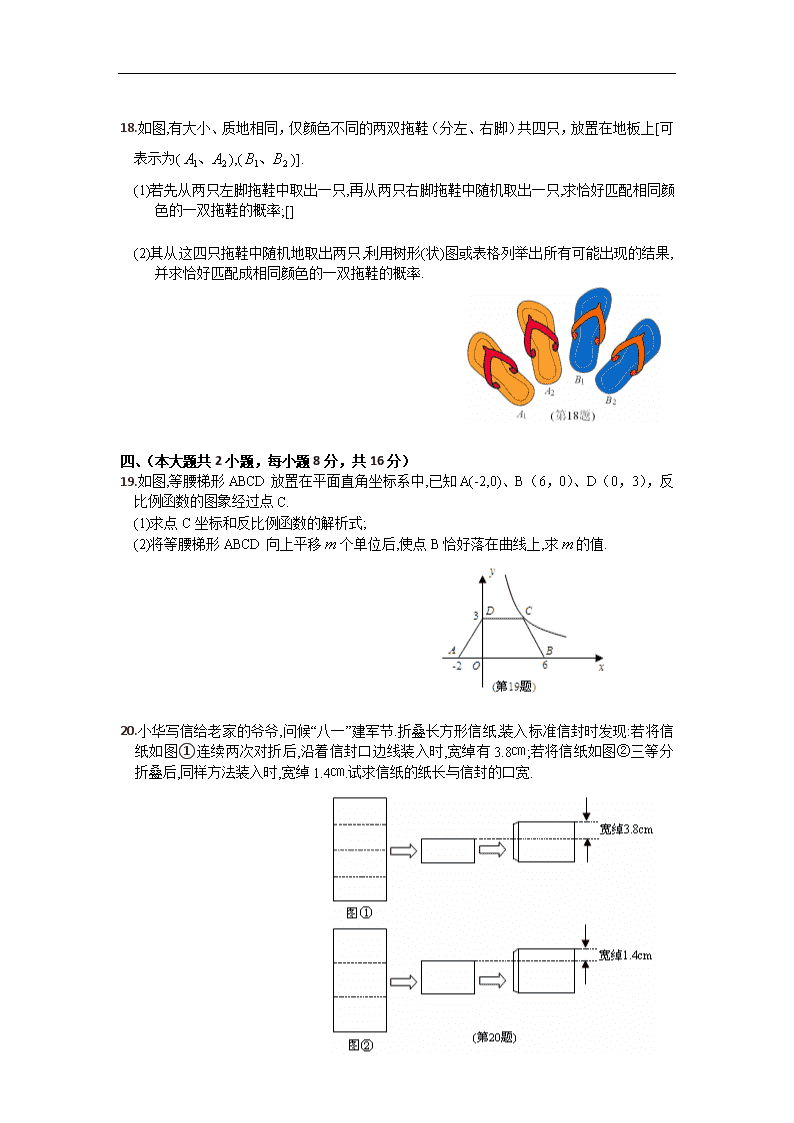
机密★2012年6月19日 江西省2012年初中毕业暨中等学校招生考试 数学试题 说明：‎ ‎1.本卷共有六个大题，24个小题，全卷满分120分，考试时间120分钟.‎ ‎ 2.本卷分为试题卷和答题卷，答案要求写在答题卷上，不得在试题卷上作答，否则不给分.‎ 一、选择题（共6小题，每小题3分，满分18分）‎ ‎1.-1的绝对值是（　　）‎ ‎ A.2 B‎.0 ‎C.﹣1 D.+1‎ ‎2.等腰三角形的顶角为80°,则它的底角是（　　）‎ ‎ A.20° B.50° C.60° D.80°‎ ‎3.下列运算正确的是（ ）.‎ A. B. C. D.‎ ‎4.如图,有a、b、c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线（ ）‎ A.a户最长 B. b户最长 C. c户最长 D.三户一样长 ‎ ‎ ‎5.如图,如果在阳光下你的身影的方向为北偏东60°方向,那么太阳相对于你的方向是（　　）‎ ‎ A.南偏西60° B.南偏西30° C.北偏东60° D.北偏东30°‎ ‎6.某人驾车从A地上高整公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油‎40升,到B地后发现油箱中还剩油‎4升,则从出发后B地油箱中所剩油(升)与时间(小时)之间函数大致图形是( )‎ 二、填空题（共8小题，每小题3分，满分24分）‎ ‎7.一个正方体有 个面.‎ ‎8.当时,的值是 .‎ ‎9.如图,AC经过⊙O的圆心O,AB与⊙O相切于点B,若∠A=50°,则∠C= 度.‎ ‎10.已知关于的一元二次方程有两个相等的实数根,则的值是 .‎ ‎11.已知,则= .‎ ‎12.已知一次函数(≠0)经过(2,-1),(-3,4)两点,则它的图象不经过第 象限.‎ ‎13.如图,已知正五边形ABCDE,请用无刻度的直尺,准确画出它的一条对称轴(保留画图痕迹).‎ ‎14.如图正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 .‎ 三、解答题（共4小题，每小题6分,共24分）‎ ‎15.化简:.‎ ‎16.解不等式组:并将解集在数轴上表示出来.‎ ‎17.如图,已知两菱形ABCD、CEFG，其中点A、C、F在同一直线上，连接BE、DG.‎ ‎ (1)在不添加辅助线时,写出其中的两对全等三角形;‎ ‎ (2)证明:BE=DG.‎ ‎18.如图,有大小、质地相同，仅颜色不同的两双拖鞋（分左、右脚）共四只，放置在地板上[可表示为(),()].‎ ‎ (1)若先从两只左脚拖鞋中取出一只,再从两只右脚拖鞋中随机取出一只,求恰好匹配相同颜色的一双拖鞋的概率;[]‎ ‎ (2)其从这四只拖鞋中随机地取出两只,利用树形(状)图或表格列举出所有可能出现的结果,并求恰好匹配成相同颜色的一双拖鞋的概率.‎ ‎ ‎ ‎ ‎ 四、（本大题共2小题，每小题8分，共16分）‎ ‎19.如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B（6，0）、D（0，3），反比例函数的图象经过点C.‎ ‎ (1)求点C坐标和反比例函数的解析式;‎ ‎ (2)将等腰梯形ABCD向上平移个单位后,使点B恰好落在曲线上,求的值.‎ ‎20.小华写信给老家的爷爷,问候“八一”建军节.折叠长方形信纸,装入标准信封时发现:若将信纸如图①连续两次对折后,沿着信封口边线装入时,宽绰有3.8㎝;若将信纸如图②三等分折叠后,同样方法装入时,宽绰1.4㎝.试求信纸的纸长与信封的口宽.‎ 五、（本大题共2小题，每小题9分，共18分）‎ ‎21.我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,分别测量出他们的身高(单位:㎝),收集并整理如下统计表:‎ ‎ ‎ ‎ 根据以上表格信息,解答如下问题:‎ ‎ (1)计算这组数据的三个统计量:平均数、中位数和众数；‎ ‎ (2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普通身高”的是哪几位男生?说明理由;‎ ‎ (3)若该年级共有280名男生,按(2)中选定标准,请你估算出该年级男生中具有“普通身高”的人数约有多少名?‎ ‎22.如图1,小红家的阳台上放置了一个晒衣架.如图2是晒衣架的（一端的横截面）侧面示意图,立杆AB、CD相交于点O,B、D两点立于地面,经测量:AB=CD=136㎝,OA=OC=51㎝,OE=OF=34㎝,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32㎝.‎ ‎ (1)求证:AC∥BD;‎ ‎ (2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°);‎ ‎ (3)小红的连衣裙穿在衣架后的总长度达到122㎝,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.‎ ‎ (参考数据:sin61.9°≈0.882,cos61.9°≈0.471,tan28.1°≈0.533;可使用科学计算器.)‎ ‎ ‎ 六、（本大题共2小题，每小题10分，共20分）‎ ‎23.如图,已知二次函数与轴交于A、B两点（点A在点B的左边），与轴交于点C.‎ ‎ (1)写出A、B两点的坐标;‎ ‎ (2)二次函数(≠0),顶点为P.‎ ‎ ①直接写出二次函数与二次函数有关图象的两条相同的性质;‎ ‎ ②是否存在实数,使△ABP为等边三角形?如存在,请求出的值;如不存在,请说明理由;‎ ‎ ③若直线与抛物线交于E、F两点，问线段EF的长度是否发生变化？如果不会，请求出EF的长度；如果会，请说明理由.‎ ‎24.已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.‎ ‎ (1)如图2,当折叠后的AB经过圆心O时,求AB弧的长;‎ ‎ (2)如图3,当弦AB=2时,求折叠后AB弧所在圆的圆心O′到弦AB的距离;‎ ‎ (3)在图1中,再将纸片⊙O沿弦CD折叠操作.‎ ‎ ①如图4,当AB∥CD,折叠后的CD弧与AB弧所在圆外切于点P,设点O到弦AB、CD的距离之和为，求的值；‎ ‎ ②如图5，当AB与CD不平行，折叠后的CD弧与AB弧所在圆外切于点P时,设点M为AB的中点，点N为CD的中点.试探究四边形OMPN的形状,并证明你的结论.‎