中考专题辅导几何证明题总结

中考专题辅导几何证明题总结

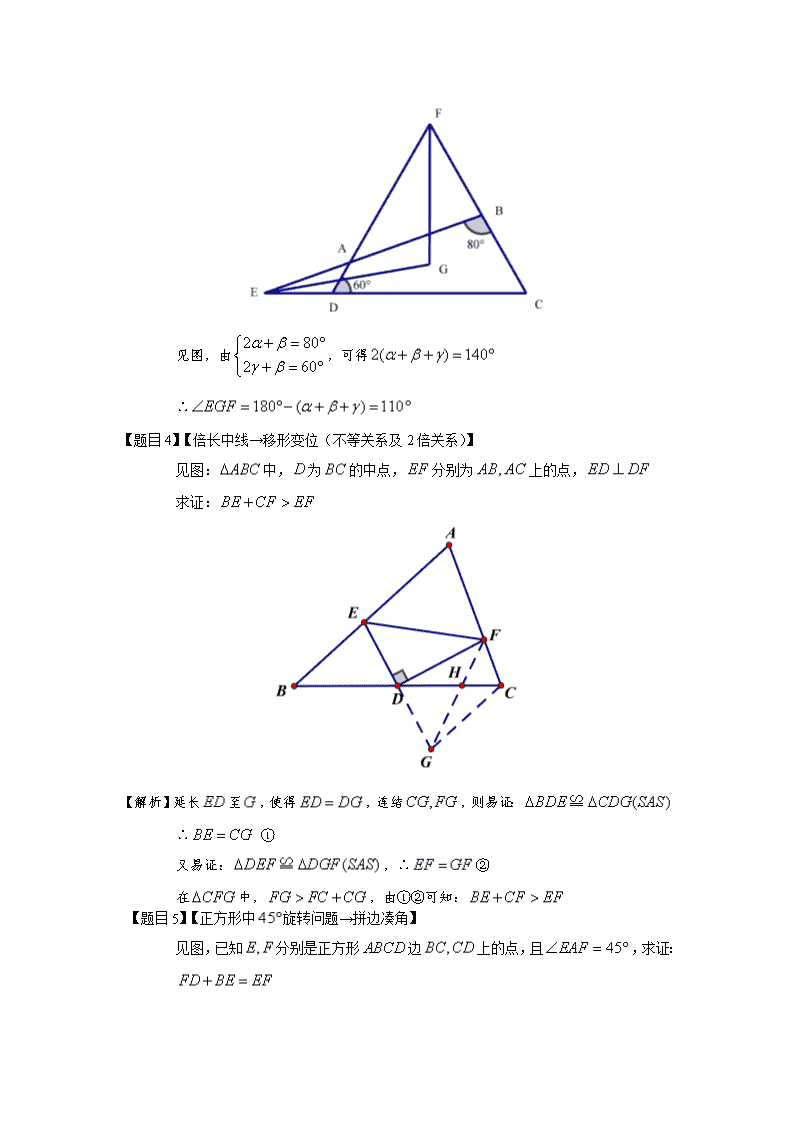
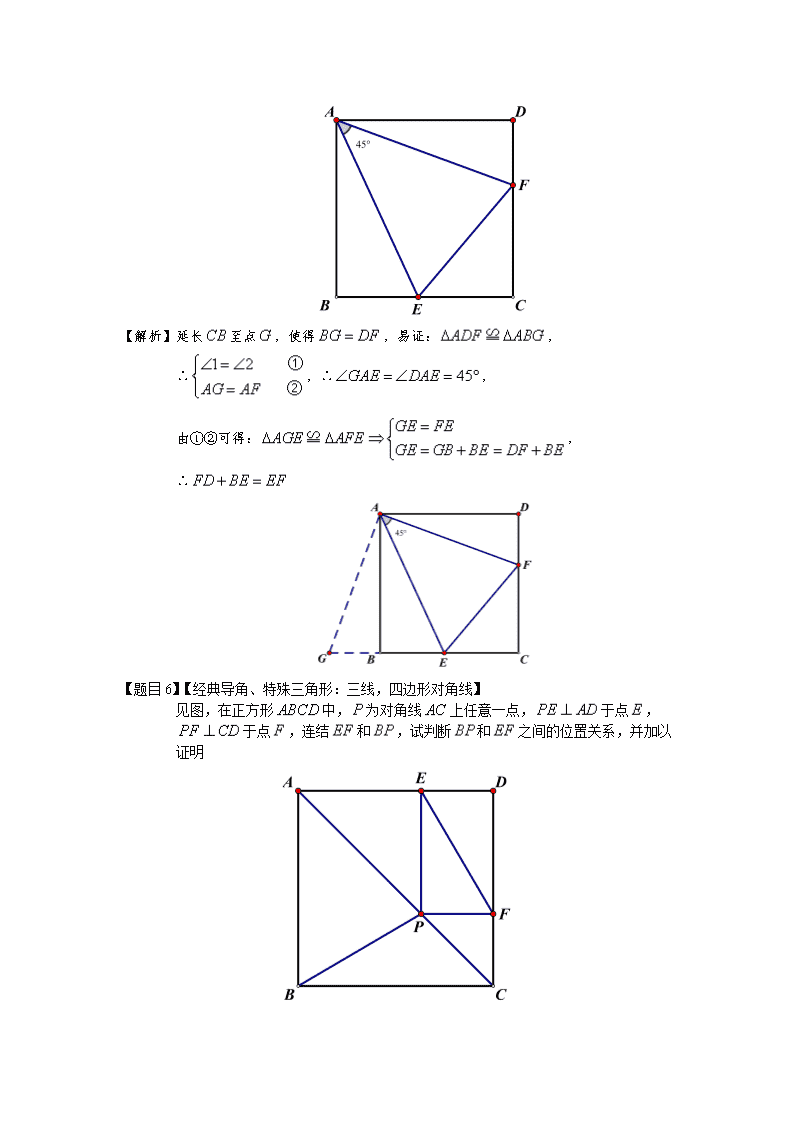
‎2014中考专题辅导几何证明题总结--数学 ‎【题目1】在锐角三角形中，三个内角的度数都是质数，则满足条件的锐角三角形仅有一个 且为等腰三角形 ‎【解析】三角形的内角和为，三个内角不可均为奇数，而且小于的质数中只有一 个偶数是，故满足条件的锐角等腰三角形有且只有一个，即：内角为 的三角形 ‎【题目2】如图，线段的长为，为上的一个动点，分别以和为斜边 在的同侧作两个等腰直角三角形和，则的长最短是________‎ ‎【答案】‎ ‎【解析】‎ 见图：∵两个三角形均为等腰三角形，∴，∴，‎ ‎∴，设，则：‎ 故：‎ ‎∴，∴的最小值为 ‎【题目3】如图，在四边形中，分别是两组对边延长线的交点，分别 平分，且，则_____________‎ ‎【答案】‎ ‎【解析】‎ 见图，由，可得 ‎∴‎ ‎【题目4】【倍长中线→移形变位（不等关系及2倍关系）】‎ 见图：中，为的中点，分别为上的点，‎ 求证：‎ ‎【解析】延长至，使得，连结，则易证：‎ ‎ ∴ ①‎ ‎ 又易证：，∴②‎ ‎ 在中，，由①②可知：‎ ‎【题目5】【正方形中旋转问题→拼边凑角】‎ 见图，已知分别是正方形边上的点，且，求证：‎ ‎【解析】延长至点，使得，易证：，‎ ‎∴，∴，‎ 由①②可得：，‎ ‎∴‎ ‎【题目6】【经典导角、特殊三角形：三线，四边形对角线】‎ 见图，在正方形中，为对角线上任意一点，于点，‎ 于点，连结和，试判断和之间的位置关系，并加以 证明 ‎【解析】连结，延长交于点，则易证 ‎∴，又为对角线，，∴，‎ 易证：，‎ 又，∴，即：‎ ‎【题目7】【经典判断：有关三角形全等】‎ ‎⑴有两边及其中一边上的高对应相等的两个三角形全等（ ）‎ ‎⑵有两边及第三边上的高对应相等的两个三角形全等（ ）‎ ‎⑶三角形6个边、角元素中，有5个元素分别相等的两个三角形全等（ ）‎ ‎⑷一边及其它两边上的高对应相等的两个三角形全等（ ）‎ ‎【答案】×，×，×，×‎ ‎【解析】见下图：‎ ‎⑴‎ ‎⑵‎ ‎⑶略，⑷略 ‎【题目8】【全等中的等积变换】‎ 见图，等腰和等腰的腰长分别为，且有共同的顶点，‎ 连结，若用与表示与的面积 求证：‎ ‎【解析】过点分别向作垂线，垂足分别为点，令，‎ ‎，，易证：，∴‎ ‎，，又，∴‎ ‎【题目9】【三角形三边与周长的关系】‎ 将长度为18的木条做成三边长均为整数的三角形，那么这样做成的不同的三角形 个数为_________‎ ‎【答案】7‎ ‎【解析】设周长为，三角形的最大边为，则，即：，则：‎ 当时，三边为：‎ 当时，三边为：‎ 当时，三边为：‎ ‎【题目10】见图，易证四边形中，，在上，且分别平分 ‎，则的长与的长的大小关系是____________‎ ‎【答案】‎ ‎【解析】方法一（截长法）：在上取，连结，易证：，‎ ‎∴，‎ 易证：，则：，‎ ‎∴，易证：‎ 方法二（补短法）：延长，使得，连结，‎ 易证：，∴，‎ 易证：，∴三点共线，在中，‎ ‎∴，∴‎ ‎【题目11】【典型类等边三角形全等】‎ 已知：，求的度数 ‎【解析】连结，，，‎ 易证：‎ 易证：‎ 综上可得：‎ ‎【题目12】已知：在中，，平分交于，过 作的垂线，交延长线于，求证：‎ ‎【解析】分别延长相交于，则：等腰，，‎ 易证：‎ ‎【题目13】三角形三边长为，且满足关系式：，试判断这个三 角形的特征，写出你的结论并加以证明 ‎【解析】∵ ‎ ‎∴‎ ‎∴，∴三者中至少有两个相等 ‎∴三角形一定是等腰三角形 ‎【题目14】已知：见图，，经过点，于，‎ 于，求证：‎ ‎ ‎ ‎【题目15】已知：如图，，和是等腰直角三角形，‎ ‎，求四边形的面积 ‎【解析】过作的垂线，垂足分别为：，则易证：‎ ‎，，∴‎ ‎∴‎ ‎【题目15】如图，四边形中，，‎ ‎，求的度数 ‎【解析】根据题意易得：，，‎ 作，连结，易得：为正三角形，∴‎ ‎∴，∴，，‎ ‎∴，∴，∴，‎ ‎【题目16】【外角定理，证明角之间的关系】‎ 如图所示：已知为内的任意一点，求证：‎ ‎【解析】‎ ‎【题目17】设为内的一点，若，证明：‎ ‎【解析】‎ ‎【题目18】【利用中位线解题】‎ 如图，在中，，为的中点，为边上一点，‎ 且，求的长 ‎【解析】‎ ‎【题目19】【构造等边三角形→等腰三角形+】‎ 如图所示，两条长度为的线段和相交于点，且，‎ 求证：‎ ‎【解析】‎ ‎【题目20】【代数方程与根的判别式】‎ 求方程的实数根 ‎【解析】将方程看成关于的一元二次方程，则方程有解的条件为：‎ ‎，又，∴，代入方程得：‎ ‎，解得：‎ ‎【题目21】【特殊双十字分解法】‎ 解方程：‎ ‎【解析】用双十字相乘法：‎ 故分解为：，‎ 解得：或