- 2021-04-21 发布 |
- 37.5 KB |
- 20页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
河北省衡水中学2020届高三上学期四调考试数学(文)试题
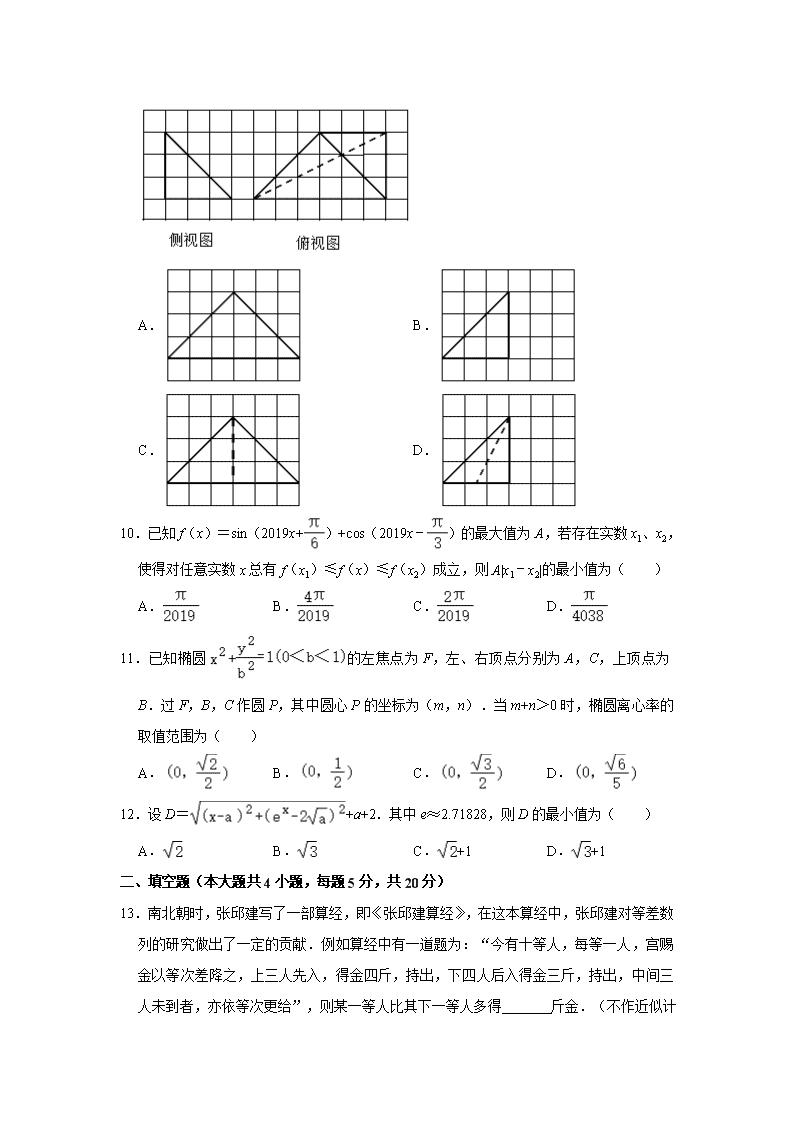
2019-2020学年河北省衡水中学高三(上)四调数学试卷(文科) 一、选择题(本大题共12小题,每题5分,共60分,下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上) 1.设集合M={﹣1,2,3},N={a+2,a2+2},且M∩N={3},则实数a的值为( ) A.1或﹣1 B.﹣1 C.1 D.2 2.AB是抛物线y2=2x的一条焦点弦,|AB|=4,则AB中点C的横坐标是( ) A.2 B. C. D. 3.已知{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,那么a3+a5的值等于( ) A.5 B.10 C.15 D.20 4.与双曲线有共同的渐近线,且经过点A(﹣3,)的双曲线的一个焦点到一条渐近线的距离是( ) A.8 B.4 C.2 D.1 5.△ABC是边长为2的等边三角形,已知向量,满足=2,=2+,则下列结论正确的是( ) A.||=1 B.⊥ C.•=1 D.(4+)⊥ 6.存在函数f(x)满足,对任意x∈R都有( ) A.f(sin2x)=sinx B.f(sin2x)=x2+x C.f(x2+1)=|x+1| D.f(x2+2x)=|x+1| 7.已知双﹣y2=1(a>0)的左、右焦点分别曲线为F1,F2,离心率为,P为双曲线右支上一点,且满足|PF1|2﹣|PF2|2=4,则△PF1F2的周长为( ) A.2 B.2+2 C.2+4 D.2+4 8.已知函数f(x)为R上的可导函数,其导函数为f'(x),且f(x)=,在△ABC中,f(A)=f'(B)=1,则△ABC的形状为( ) A.等腰锐角三角形 B.直角三角形 C.等边三角形 D.等腰钝角三角形 9.如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( ) A. B. C. D. 10.已知f(x)=sin(2019x+)+cos(2019x﹣)的最大值为A,若存在实数x1、x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1﹣x2|的最小值为( ) A. B. C. D. 11.已知椭圆的左焦点为F,左、右顶点分别为A,C,上顶点为B.过F,B,C作圆P,其中圆心P的坐标为(m,n).当m+n>0时,椭圆离心率的取值范围为( ) A. B. C. D. 12.设D=+a+2.其中e≈2.71828,则D的最小值为( ) A. B. C.+1 D.+1 二、填空题(本大题共4小题,每题5分,共20分) 13.南北朝时,张邱建写了一部算经,即《张邱建算经》,在这本算经中,张邱建对等差数列的研究做出了一定的贡献.例如算经中有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,得金四斤,持出,下四人后入得金三斤,持出,中间三人未到者,亦依等次更给”,则某一等人比其下一等人多得 斤金.(不作近似计算) 14.已知直线l经过抛物线C:y=的焦点F,与抛物线交于A,B,且xA+xB=8,点D是弧AOB(O为原点)上一动点,以D为圆心的圆与直线l相切,当圆D的面积最大时,圆D的标准方程为 . 15.如图(1),在等腰直角△ABC中,斜边AB=4,D为AB的中点,将△ACD沿CD折叠得到如图(2)所示的三棱锥C﹣A'BD,若三棱锥C﹣A'BD的外接球的半径为,则∠A'DB= . 16.已知△ABC的三边分别为a,b,c,所对的角分别为A,B,C,且满足,且△ABC的外接圆的面积为3π,则f(x)=cos2x+4(a+c)sinx+1的最大值的取值范围为 三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17.已知等差数列{an}满足:a3=7,a5+a7=26.{an}的前n项和为Sn. (Ⅰ)求an及Sn; (Ⅱ)令bn=(n∈N*),求数列{bn}的前n项和Tn. 18.如图,在平面四边形ABCD中,已知AB=BC=CD=2,AD=2. (1)求cosA﹣cosC的值; (2)记△ABD与△BCD的面积分别为S1,S2,求S12+S22的最大值. 19.已知抛物线C的方程y2=2px(p>0),焦点为F,已知点P在C上,且点P到点F 的距离比它到y轴的距离大1. (1)试求出抛物线C的方程; (2)若抛物线C上存在两动点M,N(M,N在对称轴两侧),满足OM⊥ON(O为坐标原点),过点F作直线交C于A,B两点,若AB∥MN,线段MN上是否存在定点E,使得=4恒成立?若存在,请求出E的坐标,若不存在,请说明理由. 20.椭圆的离心率是,过点P(0,1)做斜率为k的直线l,椭圆E与直线l交于A,B两点,当直线l垂直于y轴时. (Ⅰ)求椭圆E的方程; (Ⅱ)当k变化时,在x轴上是否存在点M(m,0),使得△AMB是以AB为底的等腰三角形,若存在求出m的取值范围,若不存在说明理由. 21.设抛物线Γ的方程为y2=2px,其中常数p>0,F是抛物线Γ的焦点. (1)若直线x=3被抛物线Γ所截得的弦长为6,求p的值; (2)设A是点F关于顶点O的对称点,P是抛物线Γ上的动点,求的最大值; (3)设p=2,l1,l2是两条互相垂直,且均经过点F的直线,l1与抛物线Γ交于点A,B,l2与抛物线Γ交于点C,D,若点G满足4=+++,求点G的轨迹方程. 22.已知函数. (1)讨论f(x)的单调性. (2)试问是否存在a∈(﹣∞,e],使得,对x∈[1,+∞)恒成立?若存在,求a的取值范围;若不存在,请说明理由. 2019-2020学年河北省衡水中学高三(上)四调数学试卷(文科) 参考答案与试题解析 一、选择题(本大题共12小题,每题5分,共60分,下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上) 1.设集合M={﹣1,2,3},N={a+2,a2+2},且M∩N={3},则实数a的值为( ) A.1或﹣1 B.﹣1 C.1 D.2 【解答】解:∵M={﹣1,2,3},N={a+2,a2+2},且M∩N={3}, ∴a+2=3,或a2+2=3,解得a=1或﹣1, a=1时不满足集合元素的互异性,a=1舍去, ∴a=﹣1. 故选:B. 2.AB是抛物线y2=2x的一条焦点弦,|AB|=4,则AB中点C的横坐标是( ) A.2 B. C. D. 【解答】解:设A(x1,y1),B(x2,y2)根据抛物线的定义可知 |AB|=x1+x2+p=x1+x2+1=4, ∴=, 故选:C. 3.已知{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,那么a3+a5的值等于( ) A.5 B.10 C.15 D.20 【解答】解:由等比数列的性质得:a2•a4=a32,a4•a6=a52 ∴a2a4+2a3a5+a4a6=25可化为 (a3+a5)2=25又∵an>0 ∴a3+a5=5 故选:A. 4.与双曲线有共同的渐近线,且经过点A(﹣3,)的双曲线的一个焦点到一条渐近线的距离是( ) A.8 B.4 C.2 D.1 【解答】解:∵与双曲线有共同的渐近线, ∴设双曲线方程为 , 将点 代入双曲线方程, 解得 ,⇒ 从而所求双曲线方程的焦点坐标为(,0),一条渐近线方程为 , 所以焦点到一条渐近线的距离是=2, 故选:C. 5.△ABC是边长为2的等边三角形,已知向量,满足=2,=2+,则下列结论正确的是( ) A.||=1 B.⊥ C.•=1 D.(4+)⊥ 【解答】解:因为已知三角形ABC的等边三角形,,满足=2,=2+,又,∴的方向应该为的方向. 所以,, 所以=2,=1×2×cos120°=﹣1, 4=4×1×2×cos120°=﹣4,=4,所以=0,即(4)=0,即=0,所以; 故选:D. 6.存在函数f(x)满足,对任意x∈R都有( ) A.f(sin2x)=sinx B.f(sin2x)=x2+x C.f(x2+1)=|x+1| D.f(x2+2x)=|x+1| 【解答】解:A.取x=0,则sin2x=0,∴f(0)=0; 取x=,则sin2x=0,∴f(0)=1; ∴f(0)=0,和1,不符合函数的定义; ∴不存在函数f(x),对任意x∈R都有f(sin2x)=sinx; B.取x=0,则f(0)=0; 取x=π,则f(0)=π2+π; ∴f(0)有两个值,不符合函数的定义; ∴该选项错误; C.取x=1,则f(2)=2,取x=﹣1,则f(2)=0; 这样f(2)有两个值,不符合函数的定义; ∴该选项错误; D.令x+1=t,则f(x2+2x)=|x+1|,化为f(t2﹣1)=|t|; 令t2﹣1=x,则t=±; ∴; 即存在函数f(x)=,对任意x∈R,都有f(x2+2x)=|x+1|; ∴该选项正确. 故选:D. 7.已知双﹣y2=1(a>0)的左、右焦点分别曲线为F1,F2,离心率为,P为双曲线右支上一点,且满足|PF1|2﹣|PF2|2=4,则△PF1F2的周长为( ) A.2 B.2+2 C.2+4 D.2+4 【解答】解:由题意可得b=1,c=, 即有e==, 可得a=,c=2, P为双曲线右支上一点, 可得|PF1|﹣|PF2|=2a=2, 又|PF1|2﹣|PF2|2=4, 可得|PF1|+|PF2|=2, 则△PF1F2的周长为2+2c=4+2, 故选:C. 8.已知函数f(x)为R上的可导函数,其导函数为f'(x),且f(x)=,在△ABC中,f(A)=f'(B)=1,则△ABC的形状为( ) A.等腰锐角三角形 B.直角三角形 C.等边三角形 D.等腰钝角三角形 【解答】解:函数的导数f′(x)=f′()cosx﹣sinx, 则f′()=f′()cos﹣sin=×f′()﹣=f′()﹣, 则f′()=,则f′()=1, 则f′(x)=cosx﹣sinx=2cos(x+), f(x)=sinx+cosx=2cos(x﹣), ∵f(A)=f'(B)=1, ∴f′(B)=2cos(B+)=1,即cos(B+)=, 则B+=,得B=, f(A)=2cos(A﹣)=1,即cos(A﹣)=, 则A﹣=,则A=, 则C=π﹣﹣=, 则B=C, 即△ABC是等腰钝角三角形, 故选:D. 9.如图,网格纸的各小格都是正方形,粗线画出的是一个三棱锥的侧视图和俯视图,则该三棱锥的正视图可能是( ) A. B. C. D. 【解答】解:由已知中锥体的侧视图和俯视图, 可得该几何体是三棱锥, 由侧视图和俯视图可得,该几何的直观图如图P﹣ABC所示: 顶点P在以BA和BC为邻边的平行四边形ABCD上的射影为CD的中点O, 故该锥体的正视图是: 故选:A. 10.已知f(x)=sin(2019x+)+cos(2019x﹣)的最大值为A,若存在实数x1、x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1﹣x2|的最小值为( ) A. B. C. D. 【解答】解:依题意f(x)=sin2019xcos+cos2019xsin+cos2019xcos+sin2019xsin =sin2019x+cos2019x =2sin(2019x+), ∴A=2,T=, ∴|x1﹣x2|min==, ∴A|x1﹣x2|的最小值为, 故选:C. 11.已知椭圆的左焦点为F,左、右顶点分别为A,C,上顶点为B.过F,B,C作圆P,其中圆心P的坐标为(m,n).当m+n>0时,椭圆离心率的取值范围为( ) A. B. C. D. 【解答】解:如图所示, 线段FC的垂直平分线为:x=, 线段BC的中点(,). ∵kBC=﹣b, ∴线段BC的垂直平分线的斜率k=. ∴线段BC的垂直平分线方程为:y﹣=(x﹣), 把x==m代入上述方程可得:y==n. ∵m+n>0, ∴>0. 化为:b>,又0<b<1, 解得<b<1. ∴e==c=∈(0,). 故选:A. 12.设D=+a+2.其中e≈2.71828,则D的最小值为( ) A. B. C.+1 D.+1 【解答】解:由题意可得a≥0,D=+a+2, 由表示两点C(x,ex)与点A(a,2)的距离, 而A在抛物线y2=4x(x≥0)上,抛物线的焦点F(1,0),准线为x=﹣1, 则D表示A与C的距离和A与准线的距离的和再加上1, 由抛物线的定义可得D表示A与C的距离和A与F的距离的和再加上1, 由图象可得当F,A,C三点共线,且QF为曲线y=ex的法线,D取得最小值, 即Q为切点,设为(m,em), 由•em=﹣1,可得m+e2m=1, 设g(m)=m+e2m,则g(m)递增,且g(0)=1, 可得切点Q(0,1), 即有|FQ|==, 则D的最小值为+1. 故选:C. 二、填空题(本大题共4小题,每题5分,共20分) 13.南北朝时,张邱建写了一部算经,即《张邱建算经》,在这本算经中,张邱建对等差数列的研究做出了一定的贡献.例如算经中有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,得金四斤,持出,下四人后入得金三斤,持出,中间三人未到者,亦依等次更给”,则某一等人比其下一等人多得 斤金.(不作近似计算) 【解答】解:设第十等人得金a1斤,第九等人得金a2斤,以此类推,第一等人得金a10斤, 则数列{an}构成等差数列,设公差为d,则每一等人比下一等人多得d斤金, 由题意得,即, 解得d=, 所以每一等人比下一等人多得斤金. 14.已知直线l经过抛物线C:y=的焦点F,与抛物线交于A,B,且xA+xB=8,点D是弧AOB(O为原点)上一动点,以D为圆心的圆与直线l相切,当圆D的面积最大时,圆D的标准方程为 (x﹣4)2+(y﹣4)2=5 . 【解答】解:抛物线的标准方程为x2=4y,抛物线的焦点坐标为F(0,1), 直线AB的斜率k===(xA+xB)==2, 则l的方程为y=2x+1,即2x﹣y+1=0, 点D到直线l距离最大时,圆D的面积最大, 令y′==2,解得x=4,此时y=4,即D(4,4)到直线l距离最大,此时d===, 所以所求圆的标准方程为(x﹣4)2+(y﹣4)2=5, 故答案为:(x﹣4)2+(y﹣4)2=5. 15.如图(1),在等腰直角△ABC中,斜边AB=4,D为AB的中点,将△ACD沿CD折叠得到如图(2)所示的三棱锥C﹣A'BD,若三棱锥C﹣A'BD的外接球的半径为,则∠A'DB= . 【解答】 解:球是三棱锥C﹣A'BD的外接球,所以球心O到各顶点的距离相等,如图. 根据题意,CD⊥平面A'BD, 取CD的中点E,A'B的中点G,连接CG,DG, 因为A'D=BD,CD⊥平面A'BD, 所以A'和B关于平面CDG对称, 在平面CDG内,作线段CD的垂直平分线,则球心O在线段CD的垂直平分线上,设为图中的O点位置,过 O作直线CD的平行线,交平面A'BD于点F, 则OF⊥平面A'BD,且OF=DE=1, 因为A'F在平面A'BD内,所以OF⊥A'F, 即三角形A'OF为直角三角形,且斜边OA'=R=, ∴A'F===2, 所以,BF=2, 所以四边形A'DBF为菱形, 又知OD=R,三角形ODE为直角三角形, ∴OE===2, ∴三角形A'DF为等边三角形, ∴∠A'DF=, 故∠A'DB=, 故填:. 16.已知△ABC的三边分别为a,b,c,所对的角分别为A,B,C,且满足,且△ABC的外接圆的面积为3π,则f(x)=cos2x+4(a+c)sinx+1的最大值的取值范围为 (12,24] 【解答】解:由, 可得:=, 可得a2+2b2+c2+2ac+3ab+3bc=3ab+3b2+3ac+3bc, 即a2+c2﹣b2=ac,那么2ac•cosB=ac, 即cosB=∵0<B<π,∴B=. ∵△ABC的外接圆的面积为3π,∴△ABC的外接圆的半径为R=, ∴, a+c=2R(sinA+sinc)=6sin(A+). ∵A,∴a+c∈(3,6], f(x)=cos2x+4(a+c)sinx+1=﹣2sin2x++4(a+c)sinx+2 令g(t)=﹣2t2+4(a+c)t+2,t∈[﹣1,1], g(t)在[﹣1,1]单调递增,∴g(t)max=g(1)=4(a+c)∈(12,24] 则f(x)=cos2x+4(a+c)sinx+1的最大值的取值范围为(12,24]' 故答案为:(12,24]. 三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17.已知等差数列{an}满足:a3=7,a5+a7=26.{an}的前n项和为Sn. (Ⅰ)求an及Sn; (Ⅱ)令bn=(n∈N*),求数列{bn}的前n项和Tn. 【解答】解:(Ⅰ)设等差数列{an}的公差为d, ∵a3=7,a5+a7=26, ∴,解得a1=3,d=2, ∴an=3+2(n﹣1)=2n+1; Sn==n2+2n. (Ⅱ)===, ∴Tn===. 18.如图,在平面四边形ABCD中,已知AB=BC=CD=2,AD=2. (1)求cosA﹣cosC的值; (2)记△ABD与△BCD的面积分别为S1,S2,求S12+S22的最大值. 【解答】解:(1)在△ABD中,BD2=AD2+AB2﹣2AD•AB•cosA=12﹣8cosA, 在△BDC中,BD2=BC2+CD2﹣2BC•CD•cosC, 所以12﹣8cosA=8﹣8cosC, 整理得. (2)由题意知:=8sin2A,, 所以=8sin2A+4sin2C== =, 由于,所以, 故,解得. 当cosA=时,. 19.已知抛物线C的方程y2=2px(p>0),焦点为F,已知点P在C上,且点P到点F的距离比它到y轴的距离大1. (1)试求出抛物线C的方程; (2)若抛物线C上存在两动点M,N(M,N在对称轴两侧),满足OM⊥ON(O为坐标原点),过点F作直线交C于A,B两点,若AB∥MN,线段MN上是否存在定点E,使得=4恒成立?若存在,请求出E的坐标,若不存在,请说明理由. 【解答】解:(1)由题意和抛物线定义可得=1,即p=2, ∴抛物线的方程为y2=4x, (2)由题意可知,kMN≠0, 设M(y12,y1),N(y22,y2),(y2>y1), 由OM⊥ON, ∴y12y22+y1y2=0,即y1y2=﹣16, 直线MN的斜率k==, ∴直线MN的方程为y﹣y1=(x﹣),即y=(x﹣4), 直线AB,①斜率存在,设斜率为k,则y=k(x﹣1),与C联立可得ky2﹣4y﹣4k=0, ∴|AB|=•=4(1+), 设点E存在,并设为E(x0,y0), 则|EM|•|EN|=(y0﹣y1)(y2﹣y0)=(1+)[﹣y1y2﹣y02+(y1+y2)y0]=(1+)(16﹣y02+), ∵=4, ∴16﹣y02+=16, 解得y0=0,y0=(不是定点,舍去), 则点E(4,0),经检验,此点满足y2<4x,所以在线段MN上, ②若斜率不存在,则|AB|=4,|EM|•|EN|=4×4=16,此时点E(4,0)满足题意, 综上所述,定点为(4,0) 20.椭圆的离心率是,过点P(0,1)做斜率为k的直线l,椭圆E与直线l交于A,B两点,当直线l垂直于y轴时. (Ⅰ)求椭圆E的方程; (Ⅱ)当k变化时,在x轴上是否存在点M(m,0),使得△AMB是以AB为底的等腰三角形,若存在求出m的取值范围,若不存在说明理由. 【解答】解:(Ⅰ)由已知椭圆过点,可得, 解得a2=9,b2=4所以椭圆的E方程为. (Ⅱ)设A(x1,y1),B(x2,y2),AB的中点C(x0,y0) 由消去y得(4+9k2)x2+18kx﹣27=0, 所以. 当k≠0时, 设过点C且与l垂直的直线方程, 将M(m,0)代入得:, 若k>0,则, 若k<0,则 所以或, 当k=0时,m=0 综上所述,存在点M满足条件,m取值范围是. 21.设抛物线Γ的方程为y2=2px,其中常数p>0,F是抛物线Γ的焦点. (1)若直线x=3被抛物线Γ所截得的弦长为6,求p的值; (2)设A是点F关于顶点O的对称点,P是抛物线Γ上的动点,求的最大值; (3)设p=2,l1,l2是两条互相垂直,且均经过点F的直线,l1与抛物线Γ交于点A,B,l2与抛物线Γ交于点C,D,若点G满足4=+++,求点G的轨迹方程. 【解答】解:(1)由x=3可得y=±,可得2=6,解得p=; (2)A是点F(,0)关于顶点O的对称点,可得A(﹣,0), 设过A的直线为y=k(x+),k=tanα, 联立抛物线方程可得k2x2+(k2p﹣2p)x+=0, 由直线和抛物线相切可得△=(k2p﹣2p)2﹣k4p2=0,解得k=±1, 可取k=1,可得切线的倾斜角为45°, 由抛物线的定义可得==,而α的最小值为45°, 的最大值为; (3)由y2=4x,可得F(1,0),设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),G(x,y), 设l1:y=k(x﹣1),联立抛物线y2=4x,可得k2x2﹣(2k2+4)x+k2=0, 即有x1+x2=2+,y1+y2=k(x1+x2)﹣2k=, 由两直线垂直的条件,可将k换为﹣,可得 x3+x4=2+4k2,y3+y4=﹣4k, 点G满足4=+++, 可得4(x,y)=(x1+x2+x3+x4﹣4,y1+y2+y3+y4), 即为4x=x1+x2+x3+x4﹣4=4k2+, 4y=y1+y2+y3+y4=﹣4k+, 可得y2=(k﹣)2=k2+﹣2=x﹣2, 则G的轨迹方程为y2=x﹣2. 22.已知函数. (1)讨论f(x)的单调性. (2)试问是否存在a∈(﹣∞,e],使得,对x∈[1,+∞)恒成立?若存在,求a的取值范围;若不存在,请说明理由. 【解答】解:(1)f′(x)=xlnx﹣alnx+a﹣x=(x﹣a)(lnx﹣1),x∈(0,+∞), ①当a≤0时,由f′(x)>0,解得x>e,由f′(x)<0,解得0<x<e, ∴f(x)在(0,e)上单调递减,在(e,+∞)上单调递增, ②0<a<e时,令f′(x)=0,解得x=a,或x=e, 由f′(x)>0,解得0<x<a,或x>e,由f′(x)<0,解得a<x<e, ∴f(x)在(a,e)上单调递减,在(0,a),(e,+∞)上单调递增, ③当a=e时,f′(x)≥0恒成立,f(x)在(0,+∞)上单调递增, ④当a>e时,由f′(x)>0,解得0<x<e,或x>a,由f′(x)<0,解得e<x<a, ∴f(x)在(e,a)上单调递减,在(0,e),(a,+∞)上单调递增. (2)假设存在a∈(﹣∞,e],使得f(x)>3+sin对x∈[1,+∞)恒成立, 则f(1)=2a﹣>3+sin,即8a﹣sin﹣15>0, 设g(x)=8x﹣sin﹣15, 则g′(x)=8﹣cos>0, 则g(x)单调递增, ∵g(2)=0, ∴a>2, 当a=e时,f(x)在[1,+∞)上单调递增, ∴f(x)min=f(1), ∴a>2,从而a=e满足题意, 当2<a<e时,f(x)在(a,e)上单调递减,在[1,a),(e,+∞)上单调递增, ∴, ∴,(*), 设h(x)=4ex﹣sin﹣e2﹣12, 则h′(x)=4e﹣cos>0, 则h(x)单调递增, ∵h(2)=8e﹣e2﹣13>0, ∴h(x)的零点小于2,从而不等式组(*)的解集为(2,+∞), ∴2<a<e, 综上,存在a∈(﹣∞,e],使得,对x∈[1,+∞)恒成立,且a的取值范围为(2,e].查看更多