- 2021-04-21 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021届课标版高考理科数学大一轮复习课件:2-8 函数模型及函数的综合应用(讲解部分)
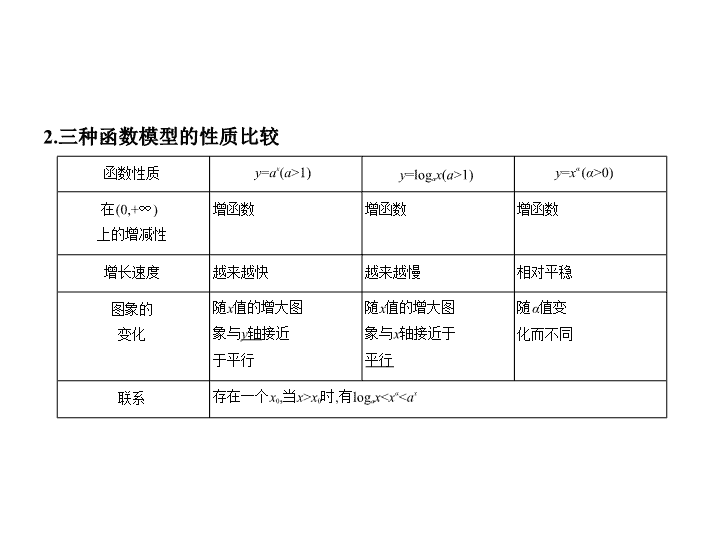
考点 函数模型及函数的综合应用 考点清单 考向基础 1.几种常见的函数模型 函数模型 函数解析式 一次函数模型 f ( x )= ax + b ( a , b 为常数, a ≠ 0) 二次函数模型 f ( x )= ax 2 + bx + c ( a , b , c 为常数, a ≠ 0) 指数函数模型 f ( x )= ba x + c ( a , b , c 为常数, a >0且 a ≠ 1, b ≠ 0) 对数函数模型 f ( x )= b log a x + c ( a , b , c 为常数, a >0且 a ≠ 1, b ≠ 0) 幂函数模型 f ( x )= ax n + b ( a , b 为常数, a ≠ 0, n ≠ 0) “对勾”函数模型 f ( x )= x + ( a >0) 函数性质 y = a x ( a >1) y =log a x ( a >1) y = x α ( α >0) 在(0,+ ∞ ) 上的增减性 增函数 增函数 增函数 增长速度 越来越快 越来越慢 相对平稳 图象的 变化 随 x 值的增大图 象与 y 轴 接近 于平行 随 x 值的增大图 象与 x 轴接近于 平行 随 α 值变 化而不同 联系 存在一个 x 0 ,当 x > x 0 时,有log a x < x α < a x 2.三种函数模型的性质比较 3.“对勾”函数的性质 函数 f ( x )= x + ( a >0). (1)该函数在(- ∞ ,- ]和[ ,+ ∞ )上单调递增,在(- ,0)和(0, )上单调递 减. (2)当 x >0时, x = 时取最小值2 ; 当 x <0时, x =- 时取最大值-2 . 考向突破 考向 函数的综合应用 例 (2019福建高考模拟,16)某公司计划投资开发一种新能源产品,预计能 获得10万元~1 000万元的收益.现准备制订一个对开发科研小组的奖励方 案:奖金 y (单位:万元)随收益 x (单位:万元)的增加而增加,且奖金总数不超过 9万元,同时奖金总数不超过收益的20%. (1)若建立奖励方案函数模型 y = f ( x ),试确定这个函数的定义域、值域和 的范围; (2)现有两个奖励函数模型:① y = +2;② y =4lg x -3.试分析这两个函数模型 是否符合公司的要求.请说明理由. 解析 (1) y = f ( x )的定义域是[10,1 000],值域是(0,9], ∈(0,0.2]. (2)当 y = +2时, = + 的最大值是 >0.2,不符合要求.当 y =4lg x -3时, 在定义域上为增函数,最大值为9. ≤ 0.2 ⇔ y -0.2 x ≤ 0. 令 g ( x )=4lg x -3-0.2 x ,则 g '( x )= <0, 所以 g ( x ) ≤ g (10)=-1<0,即 ≤ 0.2. 故函数 y =4lg x -3符合公司要求. 方法 函数的实际应用题 解决函数模型的实际应用题,首先应考虑该题考查的是哪种函数,并要注意 定义域,然后结合所给模型,列出函数关系式,最后结合其实际意义作出回 答.明确下面的基本解题步骤是解题的必要基础: 方法技巧 例 (2019湖北荆州质量检查(一),20)为响应国家提出的“大众创业,万众 创新”的号召,小李大学毕业后,决定利用所学专业进行自主创业.经过市 场调查,生产某小型电子产品需投入年固定成本为5万元,每年生产 x 万件, 需另投入流动成本为 C ( x )万元,且 C ( x )= 每件产品售价为1 0元.经市场分析,生产的产品当年能全部售完. (1)写出年利润 P ( x )(万元)关于年产量 x (万件)的函数解析式;(注:年利润=年 销售收入-固定成本-流动成本) (2)当年产量为多少万件时,小李在这一产品的生产中所获利润最大?最大 利润是多少? 解析 (1)因为每件产品售价为10元, 所以 x 万件产品的销售收入为10 x 万元, 依题意得,当0< x <8时, P ( x )=10 x - -5=- x 2 +6 x -5,当 x ≥ 8时, P ( x )=10 x - -5=30- , 所以 P ( x )= (2)当0< x <8时, P ( x )=- ( x -6) 2 +13, 当 x =6时, P ( x )取得最大值 P (6)=13, 当 x ≥ 8时, P '( x )=-1+ <0, 所以 P ( x )为减函数, 所以当 x =8时, P ( x )取得最大值 P (8)= ,因为13< , 故当年产量为8万件时,小李在这一产品的生产中所获利润最大,最大利润 为 万元.查看更多