2018-2019学年河北省遵化市高二上学期期中考试数学试题 解析版

2018-2019学年河北省遵化市高二上学期期中考试数学试题 解析版

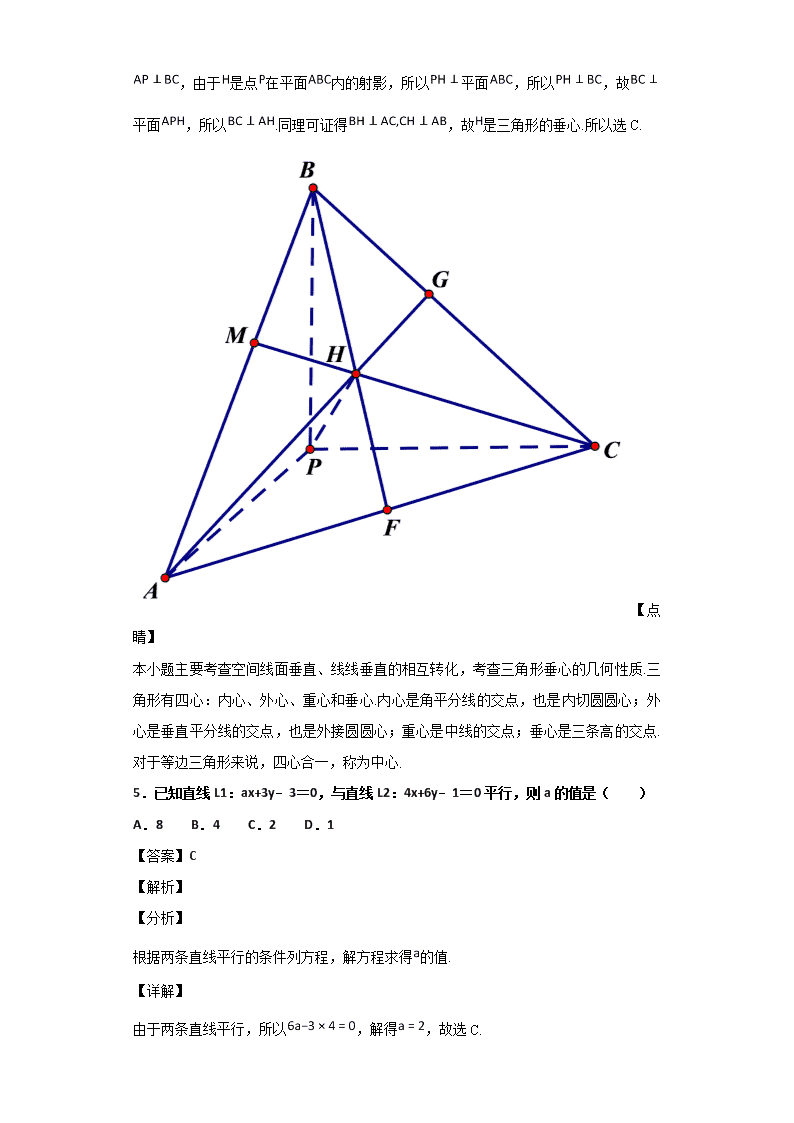
绝密★启用前 河北省遵化市 2018-2019 学年高二上学期期中考试数学试题 评卷人 得分 一、单选题 1．在直角坐标系中，直线 的倾斜角是（ ） A． B． C． D． 【答案】C 【解析】 试题分析：直线 x 的斜率等于- ,设此直线的倾斜角为 θ，则 tanθ=- ，又 0≤θ＜π，∴θ=， ,故选 C． 考点：本题主要是考查直线的倾斜角和斜率的关系，以及倾斜角的取值范围，已知三角 函数值求角的大小. 点评：解决该试题的关键是先求出直线的斜率 tanθ 的值，根据倾斜角 θ 的范围求出 θ 的大小.已知三角函数值求角是解题的难点． 2．平面 α 截球 O 的球面所得圆的半径为 1，球心 O 到平面 α 的距离为 ，则此球的 体积为 （A） π （B） π （C）4 π （D） π 【答案】B 【解析】球半径 ，所以球的体积为 ，选 B. 3．直线 x+y﹣1＝0 被圆（x+1）2+y2＝3 截得的弦长等于（　　） A． B．2 C．2 D．4 【答案】B 【解析】 3 3 0x y+ − = 6 π 3 π 5 6 π 2 3 π 3 3 0x y+ − = 3 3 3 3 5 6 π 2 6 4 3 6 6 3 3)2(1 2 =+=r ππ 34)3(3 4 3 =× 如图,圆(x＋1)2＋y2＝3 的圆心为 M(−1,0)， 圆半径|AM|= ， 圆心 M (−1,0)到直线 x+y−1=0 的距离： | ， ∴直线 x+y−1=0 被圆(x+1)2+y2=3 截得的弦长： . 故选 B. 点睛: 本题考查圆的标准方程以及直线和圆的位置关系.判断直线与圆的位置关系一般 有两种方法： 1．代数法：将直线方程与圆方程联立方程组，再将二元方 程组转化为一 元二次方程，该方程解的情况即对应直 线与圆的位置关系．这种方法具有一般性，适 合于判 断直线与圆锥曲线的位置关系，但是计算量较大． 2．几何法：圆心到直线的距 离与圆半径比较大小，即可判断直线与圆的位置关系．这种方法的特点是计算量较 小．当直线与圆相交时,可利用垂径定理得出圆心到直线的距离,弦长和半径的勾股关系. 4．已知 P 是△ABC 所在平面外一点，PA，PB，PC 两两垂直，且 P 在△ABC 所在平面内 的射影 H 在△ABC 内，则 H 一定是△ABC 的（　　） A．内心 B．外心 C．垂心 D．重心 【答案】C 【解析】 【分析】 连接 ，分别证明这是三角形 的三条高，由此确定 点为 的垂心. 【详解】 画出图像如下图所示.先证 ，由于 ，所以 平面 ，所以 ，由于 是点 在平面 内的射影，所以 平面 ，所以 ，故 平面 ，所以 .同理可证得 ，故 是三角形的垂心.所以选 C. 【点 睛】 本小题主要考查空间线面垂直、线线垂直的相互转化，考查三角形垂心的几何性质.三 角形有四心：内心、外心、重心和垂心.内心是角平分线的交点，也是内切圆圆心；外 心是垂直平分线的交点，也是外接圆圆心；重心是中线的交点；垂心是三条高的交点. 对于等边三角形来说，四心合一，称为中心. 5．已知直线 L1：ax+3y﹣3＝0，与直线 L2：4x+6y﹣1＝0 平行，则 a 的值是（　　） A．8 B．4 C．2 D．1 【答案】C 【解析】 【分析】 根据两条直线平行的条件列方程，解方程求得 的值. 【详解】 由于两条直线平行，所以 ，解得 ，故选 C. 【点睛】 本小题主要考查两条直线平行的条件.属于基础题.由于直线的斜率有可能不存在，如果 两条直线的斜率都不存在，那么这两条直线平行.当两条直线斜率都存在时，要两条直 线平行，则需要斜率相等和截距不相等，这两个条件必须同时满足.如果一条直线斜率 存在，另一条直线斜率为零，则这两条直线垂直. 6．设 l 为直线，α，β 是两个不同的平面，下列命题中正确的是 (　　)． A．若 l∥α，l∥β，则 α∥β B．若 l⊥α，l⊥β，则 α∥β C．若 l⊥α，l∥β，则 α∥β D．若 α⊥β，l∥α，则 l⊥β 【答案】B 【解析】A 中，α 与 β 可能平行，也可能相交，A 错；B 中，l⊥α，l⊥β ⇒α∥β， 正确；C 中，可得 α⊥β；C 错；D 中，可得 l∥β 或 l⊂β，或 l⊥β，D 错． 7．直线（2k﹣1）x﹣（k+3）y﹣（k﹣11）＝0（k∈R）所经过的定点是（　　） A．（5，2） B．（2，3） C．（﹣ ，3） D．（5，9） 【答案】B 【解析】 【分析】 将原方程重新合并同类项，即将含有 的项合并，其它合并，由此列方程解出定点的坐 标. 【详解】 直线方程可化为 ，故 ，解得定点坐标为 ，故 选 B. 【点睛】 本小题主要考查含有参数的直线方程经过的定点问题，主要的方法是重新合并同类项， 属于基础题. 8．一个几何体的三视图及其尺寸，如图所示，则该几何体的侧面积为（ ） A．80 B．40 C．48 D．96 【答案】A 【解析】 试题分析：三视图复原的几何体是正四棱锥，斜高是 5，底面边长是 8，侧面积为 ×4×8×5=80；故选：A． 考点：由三视图求面积、体积． 9．点 P（4，﹣2）与圆 x2+y2=4 上任一点连线的中点轨迹方程是（ ） A．（x﹣2）2+（y+1）2=1 B．（x﹣2）2+（y+1）2=4 C．（x+4）2+（y﹣2）2=1 D．（x+2）2+（y﹣1）2=1 【答案】A 【解析】 设圆上任一点坐标为(x0，y0)，则 x02＋y02＝4，连线中点坐标为(x，y)， 则 ⇒ 代入 中得(x－2)2＋(y＋1)2＝1，选 C. 10．如图，在三棱柱 中，侧棱垂直于底面，底面是边长为 2 的正三角形，侧 棱长为 3，则 与平面 所成的角是 1 2 A． B． C． D． 【答案】A 【解析】 记点 B 到平面 AB1C1 的距离为 d，BB1 与平面 AB1C1 所成角为 θ，连接 BC1，利用等体积 法，VA-BB1C1＝VB-AB1C1，即 × × ×2×3＝ d× ×2×2 ，得 d＝ ，则 sinθ＝ ＝ ，所以 θ ＝ . 11．已知圆（x﹣4）2+（y﹣4）2＝4 与直线 y＝kx 的交点为 P、Q，原点为 O，则|OP|•|OQ| 的值为（　　） A．2 B．28 C．32 D．由 k 确定 【答案】B 【解析】 【分析】 先求得通过出过原点圆的切线长，再根据切割线定理求得 值. 【详解】 设圆的圆心为 ，半径为 ，故 ，过原点圆的切线长为 . 根据切割线定理可得 . 【点睛】 本小题主要考查圆的方程，考查直线和圆的位置关系，考查切割线定理，考查运算求解 能力，属于基础题. 12．在圆 内，过点 的最长弦和最短弦分别为 和 ，则四边形 的面积为（ ） A． B． C． D． 【答案】B 【解析】分析：由过圆 内一点 的最长弦和最短弦分别为 和 ， 可知最长弦为直径，最短弦为过点 且与直径 垂直。把圆 变形标 准方程 。进而可求圆心为 ，半径 。所以 ， 由点 ，求得 。进而求得 。进 而可求四边形 的面积为 。 详解：圆 变形为 。 所以圆心为 ，半径 。 因为点 ，所以 因为过圆 内点 的最长弦和最短弦分别为 和 ， 所以 ， 。且 所以四边形 的面积为 。 故选 B。 点睛：⑴过圆内一点 A 的最长弦为过点 A 的直径，最短弦为过点 A 且与过点 A 的直径 垂直的弦； ⑵ 过圆 P 内一点 A 的最短弦长为 。 第 II 卷（非选择题) 请点击修改第 II 卷的文字说明 评卷人 得分 二、填空题 13．直线 3x+2y+5＝0 在 x 轴上的截距为_____． 【答案】 【解析】 【分析】 令 代入直线方程，求得直线在 轴上的截距. 【详解】 令 代入直线方程得 .即截距为 . 【点睛】 本小题考查直线和坐标轴的交点，直线和 轴交点的横坐标叫做横截距，和 轴交点的纵 坐标叫做纵截距. 14．如图，在正方体 ABCD﹣A1B1C1D1 中，P 为棱 DC 的中点，则 D1P 与 BC1 所在的直 线所成角的余弦值等于_____． 【答案】 【解析】 【分析】 通过平移作出两条直线所成的角，然后通过解三角形求得线线角的余弦值. 【详解】 将 平移到 ，连接 ，由于 ，故角 是两条直线所成的角，在三角形 中 ， 设 正 方 体 的 边 长 为 ， 则 ， 由 余 弦 定 理 得 . 【点睛】 本小题考查空间两条异面直线所成的角的余弦值，解决的方法是将两条异面直线通过平 行移动到一起，然后通过解三角形来求得. 15．以圆 C1：x2＋y2－12x－2y－13＝0 和圆 C2：x2＋y2＋12x＋16y－25＝0 公共弦为 直径的圆的方程为________． 【答案】x2＋y2－4x＋4y－17＝0 【解析】 试题分析：解法一：先两圆方程相减，得到公共弦方程，再联立直线和圆的方程求出公 共点坐标，进而求出圆的半径和圆心，写出圆的方程即可；解法二：先两圆方程相减， 得到公共弦方程，再利用圆系方程进行求解. 试题解析：解法一：联立两圆方程 ， 相减得公共弦所在直线方程为 4x＋3y－2＝0. 再由 ， 联立得两圆交点坐标(－1,2)、(5，－6)． ∵所求圆以公共弦为直径， ∴圆心 C 是公共弦的中点(2，－2)，半径为 ， ∴圆 C 的方程为(x－2)2＋(y＋2)2＝25. 解法二：由解法一可知公共弦所在直线方程为 4x＋3y－2＝0.设所求圆的方程为 x2＋y2 －12x－2y－13＋λ(x2＋y2＋12x＋16y－25)＝0(λ 为参数)． 可求得圆心 ． ∵圆心 C 在公共弦所在直线上， ∴ ， 解得 λ＝ . ∴圆 C 的方程为 x2＋y2－4x＋4y－17＝0. 16．如图，正方体 ABCD﹣A1B1C1D1 的棱长为 1，线段 B1D1 上有两个动点 E、F，且 EF ＝ ，则下列结论中正确的序号是_____． ①AC⊥BE　②EF∥平面 ABCD　③△AEF 的面积与△BEF 的面积相等．④三棱锥 A﹣BEF 的体积为定值 【答案】①②④ 【解析】 【分析】 利用线面垂直的性质判断①正确，利用线面平行的判定定理判断②正确，利用同底不 同高判断③错误，利用等底等高证明④正确. 【详解】 由于 ，故 平面 ，所以 ，所以①正确.由于 ， 所以 平面 ，故②正确.由于三角形 和三角形 的底边都是 ，而高前者是 到 的距离，后者是 到 的距离，这两个距离相认不相等，故③错误.由于三棱锥 的底面三角形 的面积为定值 .高是 点到平面 也即 点到平面 的距离也是定值，故三棱锥 的体积为定值.故④正确.综上所述，正确的时①②④. 【点睛】 本小题主要考查空间两条直线垂直关系的判断，考查空间线面平行的判断，考查平面图 形的面积和空间立体图形的体积的判断，属于基础题. 评卷人 得分 三、解答题 17．已知 的三个顶点坐标分别为 . （1）求边 的垂直平分线的方程； （2）求 的面积. 【答案】(1) ;(2) . 【解析】试题分析: (1)利用中点坐标公式,求出 的中点坐标,利用斜率公式,求出 . 的垂直平分线的斜率与直线 的斜率乘积为 , 可得其垂直平分线的斜率,再利用直线 方程的点斜式,写出 的垂直平分线的方程;(2)用两点间距离公式求出 的长度,利用点 到直线的距离公式求出 到 距离 ,则 ,可得 的面积. 试题解析:（1）线段 的中点 的坐标为 ,又直线的 斜率为 ,∴边 的垂直平分线的斜率为 ,故边 的垂直平分线的方程为 ,即 . （2） ,直线 的方程是 ,即 ,点 到直线 的距离 , 的面积 . 18．如图，已知圆柱底面圆的半径为 ，高为 2，AB、CD 分别是两底面的直径，AD、BC 是母线，若一支小虫从 A 点出发，从侧面爬行到 C 点，求小虫爬行的最短长度． 【答案】2 【解析】 【分析】 小虫爬行的最短长度，是半个圆柱的侧面展开矩形的对角线.通过勾股定理求得这个对 角线的长. 【详解】 解：如图，将圆柱的侧面展开，其中 AB 为底面圆周的一半， 即 AB= ,AD=2-- 则小虫爬行的最短路线为线段 AC, 在矩形 AC 中，AC= 所以小虫爬行的最短路线长度为 2 . 【点睛】 本小题主要考查圆柱的侧面展开图，考查两点间的距离公式以及分析和思考能力，属于 基础题. 19．已知圆 C：（x﹣3）2+（y﹣4）2＝4，直线 L1 过定点 A（1，0）．若 L1 与圆相切， 求 L1 的方程． 【答案】 或 【解析】 【分析】 首先判断直线 斜率不存在时，与圆是相切的，得到一条切线方程.当直线 斜率存在时， 设出直线的点斜式方程，利用圆心到直线的距离等于半径列方程，由此求得直线的斜率， 同时求出了直线 的方程. 【详解】 解：①若直线 的斜率不存在，即直线是 ，符合题意． ②若直线 斜率存在，设直线 为 ，即 ． 由题意知，圆心（3，4）到已知直线 的距离等于半径 2， 即： 解之得 ． 所求直线方程是 或 . 【点睛】 本小题主要考查直线和圆的位置关系，考查点到直线的距离公式，考查数形结合的数学 思想方法，考查方程的思想.直线和圆的位置关系有三种，相交、相切、相离.主要是根 据圆心到直线的距离来判断出来，如果圆心到直线的距离等于半径，则为相切；若小于， 则为相交，若大于，则为相离. 20．如图，在正三棱柱 ABC﹣A1B1C1 中，点 D 在边 BC 上，AD⊥C1D． （1）求证：AD⊥平面 BCC1B1； （2）如果点 E 是 C1B1 的中点，求证：A1E∥平面 ADC1． 【答案】（1）详见解析；（2）详见解析 【解析】 【分析】 （1）利用正三棱柱的性质，得到 ，而 ，由此证得 平面 . （2）通过证明四边形 是平行四边形，证得 ，从而证得 平面 . 【详解】 证明:（1）在正三棱柱中 又 AD ， ，所以 AD （2）由（Ⅰ）可得 AD ，因为三棱柱是正三棱柱，所以 AB=AC，且 D 为边 BC 的中 点。 连接 DE,因为 E 为 的中点，所以 ED ，ED , 所以四边形 ，所以 ， ，AD 所以 【点睛】 本小题主要考查线面垂直的证明，考查线面平行的证明，考查正三棱柱的几何性质，属 于中档题. 21．(本小题满分 12 分) 如图，在四棱锥 P—ABCD 中，底面 ABCD 是矩形，PA⊥平面 ABCD，AP=AB， BP=BC=2，E，F 分别是 PB,PC 的中点. (Ⅰ)证明：EF∥平面 PAD； (Ⅱ)求三棱锥 E—ABC 的体积 V. 【答案】(Ⅰ)证明见解析 (Ⅱ) VE-ABC= 【解析】本题主要考查立体几何中点线面位置关系，并以我们熟悉的四棱锥为载体，尽 管侧重推理和运算，但所用知识点不多，运算也不麻烦，对于大多考生来说还是一道送 分题． (Ⅰ) 在△PBC 中，E，F 分别是 PB，PC 的中点，∴EF∥BC. 又 BC∥AD，∴ EF∥AD, 又∵AD 平面 PAD，EF 平面 PAD,[来源:学科网] ∴EF∥平面 PAD. 1 3 ⊄ ⊄ (Ⅱ)连接 AE，AC，EC，过 E 作 EG∥PA 交 AB 于点 G, 则 EG⊥平面 ABCD,且 EG= PA. 在△PAB 中，AP=AB， PAB=90°,BP=2，∴AP=AB= ,EG= . ∴S△ABC= AB·BC= × ×2= , ∴VE-ABC= S△ABC·EG= × × = . 点评：本题是我们常见的题型，相比平时那些求角及距离的题要容易的多，并且所考知 识点不多运算也不麻烦，是一道基础题． 22．在平面直角坐标系 xOy 中，已知圆 的圆心为 Q，过点 且斜 率为 k 的直线与圆 Q 相交于不同的两点 A，B． 求 k 的取值范围； 是否存在常数 k，使得向量 与 共线？如果存在，求 k 值；如果不存在，请说 明理由． 【答案】（1） ；（2）不存在. 【解析】 试题分析：（1）圆的方程可得圆心为 ，半径为 2，圆的面积为 ,设直线 l 的方 程为 y＝kx＋2．直线 l 与圆 交于两个不同的点 A，B 等价于 ＜2， 解不等式即可求出结果．（2）设 ，则 ＋ ，由 得 ，根据韦达定理和共线定理，即可解得 ．由（2）知 1 2 ∠ 2 2 2 1 2 1 2 2 2 1 3 1 3 2 2 2 1 3 ，故可判断 的情况． 试题解析：（1）圆的方程可化为 ，可得圆心为 ，半径为 2，故圆 的面积为 ． 设直线 l 的方程为 y＝kx＋2．直线 l 与圆 交于两个不同的点 A，B 等价于 ＜2，化简得 ，解得 ，即 k 的取值范围为 ． （2）设 ，则 ＋ ＝（x1＋x2，y1＋y2），由 得 ， 解此方程得 x1,2＝ ． 则 － ，① 又 ．② 而 ， ＝（6，－2）． 所以 ＋ 与 共线等价于 ，将①②代入上式，解得 ．由 （2）知 ，故没有符合题意的常数 ． 考点：1．直线与圆的位置关系；2．平面向量共线定理．