2018届二轮复习演绎推理课件（18张)（全国通用）

2018届二轮复习演绎推理课件（18张)（全国通用）

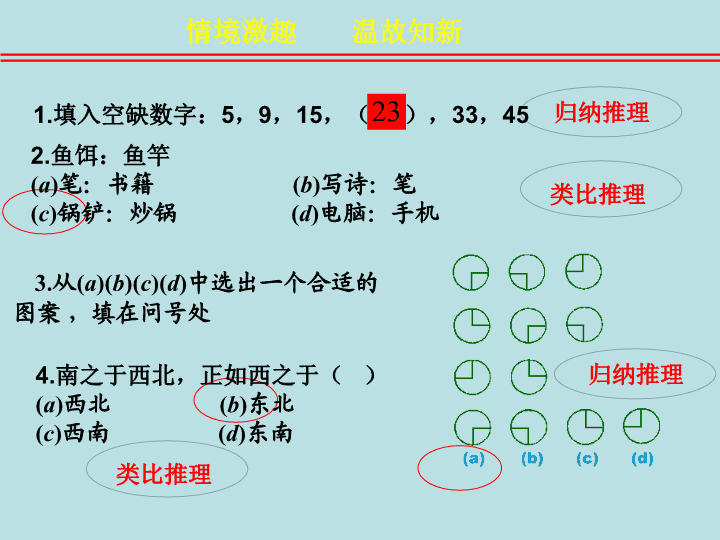
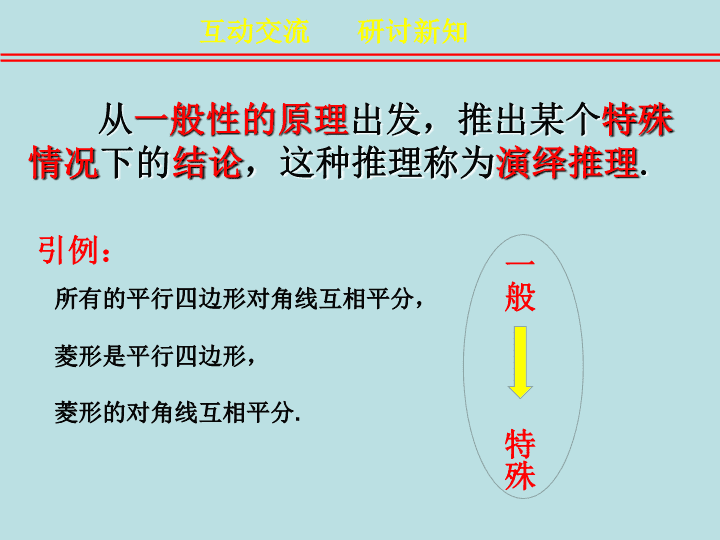
3. 从 ( a )( b )( c )( d ) 中选出一个合适的图案 ，填在问号处 情境激趣 温故知新 类比推理 归纳推理 2. 鱼饵：鱼竿 ( a ) 笔：书籍 ( b ) 写诗：笔 ( c ) 锅铲：炒锅 ( d ) 电脑：手机 1. 填入空缺数字： 5 ， 9 ， 15 ，（ ）， 33 ， 45 4. 南之于西北，正如西之于（ ） ( a ) 西北 ( b ) 东北 ( c ) 西南 ( d ) 东南 归纳推理 类比推理 引例： 所有的平行四边形对角线互相平分， 菱形是平行四边形， 菱形的对角线互相平分 . 从 一般性的原理 出发，推出某个 特殊 情况 下的 结论 ，这种推理称为 演绎推理 . 互动交流 研讨新知 一般 特殊 问题： 能否举出生活或者各科学习中，演绎推理的例子？ 互动交流 研讨新知 所有的金属都能导电， 因为铜是金属， 所以铜能导电 . 一切奇数都不能被 2 整除， 2017 是奇数， 所以 2017 不能被 2 整除 . 所有的平行四边形的对角线互相平分， 菱形是平行四边形， 菱形的对角线互相平分 . 大前题 小前题 结论 --- 已知的一般原理 --- 大前提 --- 所研究的特殊情况 ------ 小前提 --- 根据一般原理，对特殊情况做出的判断 --- 结论 互动交流 研讨新知 引例： 三段论推理 ------ 演绎推理的基本模式 问题：如何用集合的观点理解三段论推理？ 所有的平行四边形（ A ）对角线互相平分（ P ）， ---A 是 P 菱形 (B) 是平行四边形 (A) ， ---B 是 A 所以，菱形 (B) 对角线互相平分 (P). ---B 是 P A B P 若集合 A 的所有元素都具有性质 P ， B 是 A 的一个子集，那么 B 中所有元素也都具有性质 P. 概念辨析 思维升华 演绎推理的特征：当前提为真，推理形式正确时，结论必然为真 “ 三段论 ” 是由古希腊的亚里 士多德创立的，亚里士多德在西 方哲学史，逻辑学史上占有很重 要的地位，是古典形式逻辑的创 始人，在西方被称为 “ 逻辑学之父 ” ，亚里士多德提出用演绎推理的 方法来建立各门学科的体系。 延伸课堂 丰富学识 古希腊数学家欧几里 得把人们公认的一些几何 知识作为定义和公理（公 设），在此基础上研究图 形的性质，推导出一系列 定理，组成演绎体系，写 出《几何原本》，形成了 欧氏几何，按所讨论的图 形在平面上或在空间，又 分别成为 “ 平面几何 ” 与 “ 立体几何 ” 延伸课堂 丰富学识 概念辨析 思维升华 练习：将下列演绎推理写成三段论形式，并指出大，小前提及结论 1. 太阳系的大行星都以椭圆形轨道绕太阳运行 , 海王星是太阳系中的大行星 , 所以海王星以椭圆形轨道绕太阳运行 . 大前题 太阳系的大行星都以椭圆形轨道绕太阳运行 , 小前题 海王星是太阳系中的大行星 , 结论 所以海王星以椭圆形轨道绕太阳运行 . 大前题 三角函数是周期函数 2. 正切函数 y ＝ tanx 是周期函数 小前题 正切函数 y ＝ tanx 是三角函数 结论 正切函数 y ＝ tanx 是周期函数 小结：在实际使用三段论推理时，为使得语言叙述简洁， 可以省略大前提或小前提，甚至两者都可略去 . (1) 自然数是整数， 3 是自然数， 3 是整数 . 大前提错误 推理形式错误 (4) 自然数是整数， － 3 是整数， － 3 是自然数 . (3) 自然数是整数， -3 是自然数， -3 是整数 . (2) 整数是自然数， -3 是整数， -3 是自然数 . 小前提错误 概念辨析 思维升华 练习：下列推理是否正确，说明理由？ 小结：三段论推理中，（ 1 ） 大、小前提的判断必须是真实的； （ 2 ） 推理过程必须符合正确的逻辑形式和规则 . （ 1 ）中国的大学分布于中国各地， 北京大学是中国的大学， 所以北京大学分布于中国各地。 （ 2 ）有一次，德国著名诗人歌德在公园里散步。 在一条能让一个人通过的小道上，他遇到了一位 自负傲慢的批评家。两人越走越近。“我是从来 不给蠢货让路的！”批评家先开口道。“我却正好相反！”歌德说完，笑着退到路旁。 急中生智，反戈一击 言之有理，论证有据 演绎推理在生活中的应用 概念辨析 思维升华 例 1 ：已知空间四边形 ABCD 中，点 E 、 F 分别是 AB 、 AD 的中点，试判断 EF 与面 BCD 的位置关系，并证明 . 问题 : 如何应用演绎推理解决数学问题？ 数学问题的求解论证过程中，大量运用到三段论的 演绎推理模式，是我们应该熟练掌握的。 概念应用 巩固深化 关系推理 , 也是演绎推理的一种模式 , 在不等式的证明中经常用到。 概念应用 巩固深化 完全归纳推理，也是演绎推理的一种常见模式。把某类 事物所包含的每一对象一一列举出来，逐一分析论证， 进而做出关于这一类事物的一般性结论。分类讨论的思想 就是这一推理形式的具体应用。 概念应用 巩固深化 合情推理与演绎推理的区别联系 合情推理 归纳推理 类比推理 由 部分 到 整体 , 特 殊 到 一般 的推理 . 由 特殊 到 特殊 的推理 . 结论不一定正确，有待进一 步证明 . 演绎推理 由 一般 到 特殊 的 推理 . 在大前提、小前提 和推理形式都正确 的前提下，得到 的结论一定正确 . 合情推理的结论需要演绎推理的验证，而演绎 推理的方向和思路一般是通过合情推理获得的 . 区别 推理 形式 推理结论 联系 课堂总结 整体认识 作业 : 1 、课本 P34 ： 练习 A 练习 B 2 、探究生活中的演绎推理实例 课外延伸 布置作业 再 见