安徽省蚌埠市2020届高三9月第一次教学质量检查（理） 答案

安徽省蚌埠市2020届高三9月第一次教学质量检查（理） 答案

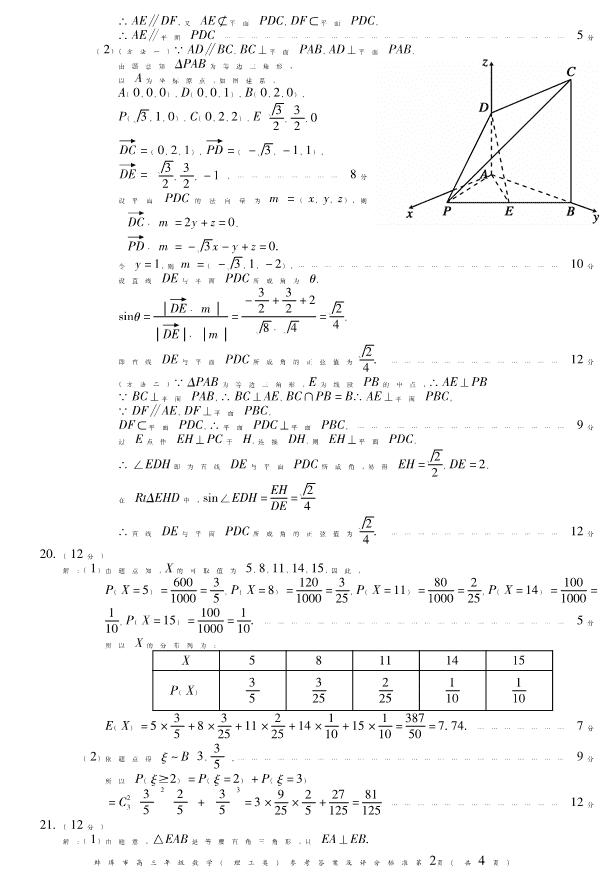
蚌埠市 ２０２０届高三年级第一次教学质量检查考试 数学（理工类）参考答案及评分标准 一、选择题： 题　号 １ ２ ３ ４ ５ ６ ７ ８ ９ １０ １１ １２ 答　案 Ｂ Ｃ Ｃ Ａ Ａ Ｄ Ａ Ｂ Ｂ Ｄ Ｄ Ｂ 二、填空题： １３７ ３　　　　１４２　　　　１５４６０８０　　　　１６２ｌｎ２ 三、解答题： １７（１０分） 解：（１）∵ｃｏｓ（Ａ－Ｂ）＝４ ５，０＜Ａ＜Ｂ＜π，所以 －π＜Ａ－Ｂ＜０， ∴ｓｉｎ（Ａ－Ｂ）＝－３ ５，ｔａｎ（Ａ－Ｂ）＝－３ ４ ２分……………………………………………… ∴ｔａｎＡ＝ｔａｎ［（Ａ－Ｂ）＋Ｂ］＝ｔａｎ（Ａ－Ｂ）＋ｔａｎＢ １－ｔａｎ（Ａ－Ｂ）ｔａｎＢ＝ －３ ４＋４ ３ １－（－３ ４）· ４ ３ ＝７ ２４ ５分…………… （２）由（１）得 ｓｉｎＡ＝７ ２５，ｓｉｎＢ＝４ ５，且 ０＜Ａ＜Ｂ＜π ２， ∴ｃｏｓＡ＝２４ ２５，ｃｏｓＢ＝３ ５ ７分………………………………………………………………… ｓｉｎＣ＝ｓｉｎ（Ａ＋Ｂ）＝ｓｉｎＡｃｏｓＢ＋ｃｏｓＡｓｉｎＢ＝７ ２５· ３ ５＋２４ ２５· ４ ５＝１１７ １２５ ８分………………… ∵ｂ＝２ ａ ｓｉｎＡ＝ ｂ ｓｉｎＢ＝ ｃ ｓｉｎＣ＝２ ４ ５ ＝５ ２， ∴ａ＋ｂ＋ｃ＝５ ２（ｓｉｎＡ＋ｓｉｎＣ）＋２＝５ ２（７ ２５＋１１７ １２５）＋２＝７６ ２５＋２＝１２６ ２５ 即△ＡＢＣ的周长为１２６ ２５ １０分……………………………………………………………… １８（１２分） 解：（１）∵Ｓｎ－２Ｓｎ－１ ＝ｎ（ｎ≥２，ｎ∈Ｎ ），　　∴Ｓｎ＋１ －２Ｓｎ＝ｎ＋１， 两式相减得 ａｎ＋１ －２ａｎ＝１（ｎ≥２）， ２分…………………………………………………… 又（ａ１ ＋ａ２）－２ａ１ ＝２且 ａ１ ＝１，解得 ａ２ ＝３，所以 ａ２ －２ａ１ ＝１． ∴ａｎ＋１ －２ａｎ＝１（ｎ∈Ｎ ）， ∴ａｎ＋１ ＋１＝２（ａｎ＋１）， ４分………………………………………………………………… 又 ａ１ ＋１＝２≠０， 所以数列｛ａｎ＋１｝是首项为 ２，公比为 ２的等比数列  ６分……………………………… （２）由（１）知 ａｎ＋１＝２ｎ∴ａｎ＝２ｎ－１， 则 ｂｎ＝ｌｏｇ２（ａｎ＋１）ａｎ＋１ ＝ｎ·２ｎ， ８分……………………………………………………… Ｔｎ＝２＋２·２２ ＋３·２３ ＋… ＋ｎ·２ｎ，　　　 　① ２Ｔｎ＝２２ ＋２·２３ ＋３·２４ ＋… ＋ｎ·２ｎ＋１，　　　② ① －②得：－Ｔｎ＝２＋２２ ＋２３ ＋… ＋２ｎ－ｎ·２ｎ＋１， 故 Ｔｎ＝（ｎ－１）·２ｎ＋１ ＋２． １２分…………………………………………………………… １９（１２分） 证明：（１）取 ＰＣ的中点 Ｆ，连接 ＤＦ，ＥＦ，因为 Ｅ为线段 ＰＢ的中点， ∴ＥＦ∥ＢＣ，且 ＥＦ＝１ ２ＢＣ＝ＡＤ， ∵ＡＤ∥ＢＣ　　∴ＥＦ瓛ＡＤ， ２分………………………………………………………… ∴四边形 ＥＦＤＡ为平行四边形 ）页４共（页１第准标分评及案答考参）类工理（学数级年三高市埠蚌 ∴ＡＥ∥ＤＦ，又 ＡＥ平面 ＰＤＣ，ＤＦ平面 ＰＤＣ， ∴ＡＥ∥平面 ＰＤＣ ５分…………………………………………………………………… （２）（方法一）∵ＡＤ∥ＢＣ，ＢＣ⊥平面 ＰＡＢ，ＡＤ⊥平面 ＰＡＢ， 由题意知 ΔＰＡＢ为等边三角形， 以 Ａ为坐标原点，如图建系， Ａ（０，０，０），Ｄ（０，０，１），Ｂ（０，２，０）， Ｐ（槡３，１，０），Ｃ（０，２，２），Ｅ 槡３ ２，３ ２，( )０ ＤＣ ＝（０，２，１），ＰＤ ＝（ 槡－ ３，－１，１）， ＤＥ ＝ 槡３ ２，３ ２，( )－１， ８分…………………… 设平面 ＰＤＣ的 法向量 为 ｍ ＝（ｘ，ｙ，ｚ），则 ＤＣ·ｍ ＝２ｙ＋ｚ＝０， ＰＤ·ｍ 槡＝－ ３ｘ－ｙ＋ｚ＝０{ ． 令 ｙ＝１，则ｍ ＝（ 槡－ ３，１，－２）， １０分…………………………………………………… 设直线 ＤＥ与平面 ＰＤＣ所成角为 θ， ｓｉｎθ＝ ＤＥ·ｍ ＤＥ · ｍ ＝ －３ ２＋３ ２＋２ 槡８·槡４ ＝槡２ ４， 即直线 ＤＥ与平面 ＰＤＣ所成角的正弦值为槡２ ４ １２分………………………………… （方法二）∵ΔＰＡＢ为等边三角形，Ｅ为线段 ＰＢ的中点，∴ＡＥ⊥ＰＢ ∵ＢＣ⊥平面 ＰＡＢ，∴ＢＣ⊥ＡＥ，ＢＣ∩ＰＢ＝Ｂ∴ＡＥ⊥平面 ＰＢＣ， ∵ＤＦ∥ＡＥ，ＤＦ⊥平面 ＰＢＣ， ＤＦ平面 ＰＤＣ，∴平面 ＰＤＣ⊥平面 ＰＢＣ， ９分………………………………………… 过 Ｅ点作 ＥＨ⊥ＰＣ于 Ｈ，连接 ＤＨ，则 ＥＨ⊥平面 ＰＤＣ， ∴∠ＥＤＨ即为直线 ＤＥ与平面 ＰＤＣ所成角，易得 ＥＨ＝槡２ ２，ＤＥ＝２， 在 ＲｔΔＥＨＤ中，ｓｉｎ∠ＥＤＨ＝ＥＨ ＤＥ＝槡２ ４ ∴直线 ＤＥ与平面 ＰＤＣ所成角的正弦值为槡２ ４ １２分………………………………… ２０（１２分） 解：（１）由题意知，Ｘ的可取值为 ５，８，１１，１４，１５，因此， Ｐ（Ｘ＝５）＝６００ １０００＝３ ５，Ｐ（Ｘ＝８）＝１２０ １０００＝３ ２５，Ｐ（Ｘ＝１１）＝ ８０ １０００＝２ ２５，Ｐ（Ｘ＝１４）＝１００ １０００＝ １ １０，Ｐ（Ｘ＝１５）＝１００ １０００＝１ １０ ５分…………………………………………………………… 所以 Ｘ的分布列为： Ｘ ５ ８ １１ １４ １５ Ｐ（Ｘ） ３ ５ ３ ２５ ２ ２５ １ １０ １ １０ Ｅ（Ｘ）＝５×３ ５＋８×３ ２５＋１１×２ ２５＋１４×１ １０＋１５×１ １０＝３８７ ５０＝７７４ ７分………………… （２）依题意得 ξ～Ｂ ３，( )３ ５ ， ９分………………………………………………………………… 所以 Ｐ（ξ２）＝Ｐ（ξ＝２）＋Ｐ（ξ＝３） ＝Ｃ２ ３( )３ ５ ２ ( )２ ５ ＋( )３ ５ ３ ＝３×９ ２５×２ ５＋２７ １２５＝８１ １２５ １２分………………………………… ２１（１２分） 解：（１）由题意，△ＥＡＢ是等腰直角三角形，且 ＥＡ⊥ＥＢ ）页４共（页２第准标分评及案答考参）类工理（学数级年三高市埠蚌 不妨设点 Ａ位于第一象限，则直线 ＥＡ的方程为 ｙ＝ｘ＋ｐ ２， 联立方程， ｙ２ ＝２ｐｘ ｙ＝ｘ＋ｐ{ ２ ，解得 ｘ＝ｐ ２ ｙ＝{ ｐ ， 所以点 Ａ（ｐ ２，ｐ），Ｂ（ｐ ２，－ｐ），Ｅ（－ｐ ２，０） ３分………………………………………… Ｓ△ＥＡＢ ＝１ ２×ｐ×２ｐ＝ｐ２ ＝４，解得 ｐ＝２， 故抛物线 Ｃ的方程为 ｙ２ ＝４ｘ ６分………………………………………………………… （２）（方法一）设 Ａ（ｘ０，ｙ０），Ｂ（ｘ０，－ｙ０），则直线 ＥＢ的方程为 ｙ＝－ ｙ０ ｘ０ ＋ｐ ２ （ｘ＋ｐ ２）， 联立方程， ｙ２ ＝２ｐｘ ｙ＝－ ｙ０ ｘ０ ＋ｐ ２ （ｘ＋ｐ ２{ ），消去 ｘ， 得关于 ｙ的方程 ｙ０ ２ｐｙ２ ＋（ｘ０ ＋ｐ ２）ｙ＋ｐｙ０ ２ ＝０， ８分………………………………………… 该方程有一个根 －ｙ０，两根之积为 ｐ２， 则另一个根为 －ｐ２ ｙ０ ，所以点 Ｄ的坐标为 ｐ３ ２ｙ２ ０ ，－ｐ２ ｙ( )０  直线 ＡＤ的斜率为 ｙ０ ＋ｐ２ ｙ０ ｘ０ －ｐ３ ２ｙ２ ０ ＝ ｙ０ ＋ｐ２ ｙ０ ｙ２ ０ ２ｐ－ｐ３ ２ｙ２ ０ ＝ ２ｐｙ０ ｙ２ ０ －ｐ２， １０分……………………………………… 所以 ＡＤ的方程为 ｙ－ｙ０ ＝ ２ｐｙ０ ｙ２ ０ －ｐ２ ｘ－ｙ２ ０ ２( )ｐ， 化简得 ｙ＝ ２ｐｙ０ ｙ２ ０ －ｐ２ ｘ－ｐ( )２ ， 所以直线 ＡＤ过定点 ｐ ２，( )０ １２分……………………………………………………… （方法二）设 Ｂ（ｘ１，ｙ１），Ｄ（ｘ２，ｙ２），Ａ（ｘ１ －ｙ１），直线 ＢＥ的方程为 ｘ＝ｎｙ－ｐ ２， 联立方程， ｙ２ ＝２ｐｘ ｘ＝ｎｙ－ｐ{ ２ ，消去 ｘ， 得关于 ｘ的方程 ｙ２ －２ｎｐｙ＋ｐ２ ＝０，所以 ｙ１ ＋ｙ２ ＝２ｎｐ，ｙ１ｙ２ ＝ｐ２， ８分…………………… 则 ｋＡＤ ＝ｙ２ ＋ｙ１ ｘ２ －ｘ１ ＝ ２ｎｐ ｎｙ２ －ｐ( )２ － ｎｙ１ －ｐ( )２ ＝ ２ｐ ｙ２ －ｙ１ ， 直线 ＡＤ的方程为 ｙ＝ ２ｐ ｙ２ －ｙ１ （ｘ－ｘ２）＋ｙ２， １０分………………………………………… 化简得 ｙ＝ ２ｐ ｙ２ －ｙ１ ｘ－ ２ｐｘ２ ｙ２ －ｙ１ ＋ｙ２ ２ －ｙ１ｙ２ ｙ２ －ｙ１ ＝ ２ｐ ｙ２ －ｙ１ ｘ－ｐ( )２ ， 所以直线 ＡＤ过定点 ｐ ２，( )０ １２分……………………………………………………… ２２（１２分） 解：（１）设切点为 ｘ０，ａｌｎｘ０ ｘ( )０ ，则切线为 ｙ－ａｌｎｘ０ ｘ０ ＝ａ（１－ｌｎｘ０） ｘ０ ２ （ｘ－ｘ０），即 ｙ＝ａ（１－ｌｎｘ０） ｘ０ ２ ｘ＋２ａｌｎｘ０ －ａ ｘ０ ２分…………………… ）页４共（页３第准标分评及案答考参）类工理（学数级年三高市埠蚌 从而 ａ（１－ｌｎｘ０） ｘ２ ０ ＝１ ２ａｌｎｘ０ －ａ ｘ０ { ＝－１ ， 消去 ａ得：ｘ０ －１＋ｌｎｘ０ －２ｘ０ｌｎｘ０ ＝０， ３分………………………………………………… 记 ｍ（ｔ）＝ｔ－１＋ｌｎｔ－２ｔｌｎｔ（ｔ＞０） 则 ｍ′（ｔ）＝１ ｔ－２ｌｎｔ－１，显然 ｍ′（ｔ）单调递减且 ｍ′（１）＝０， 所以 ｔ∈（０，１）时，ｍ′（ｔ）＞０，ｍ（ｔ）单增，ｔ∈（１，＋∞）时，ｍ′（ｔ）＜０，ｍ（ｔ）单减， 故 ｍ（ｔ）当且仅当 ｔ＝１时取到最大值，而 ｍ（１）＝０， 因而方程 ｘ０ －１＋ｌｎｘ０ －２ｘ０ｌｎｘ０ ＝０有唯一解 ｘ０ ＝１，此时 ａ＝１， 所以 ａ＝１，切点为（１，０） ６分……………………………………………………………… （２）（方法一）记 Ｆ（ｘ）＝ｅｘ－１ －ｘ，　（ｘ＞０），则 Ｆ′（ｘ）＝ｅｘ－１ －１ 当 ｘ∈（１，＋∞）时，Ｆ′（ｘ）＞０，Ｆ（ｘ）单调递增； 当 ｘ∈（０，１）时，Ｆ′（ｘ）＜０，Ｆ（ｘ）单调递减， ∴Ｆ（ｘ）≥Ｆ（１）＝１－１＝０，∴ｅｘ－１≥ｘ，即 ｇ（ｘ）≥ｘ－１① ９分…………………………… 记 Ｇ（ｘ）＝ｘ２ －ｘ－ｌｎｘ（ｘ＞０）， 则 Ｇ′（ｘ）＝２ｘ－１－１ ｘ＝２ｘ２ －ｘ－１ ｘ ＝（ｘ－１）（２ｘ＋１） ｘ ∴ｘ∈（０，１）时，Ｇ′（ｘ）＜０，Ｇ（ｘ）单调递减； ｘ∈（１，＋∞）时，Ｇ′（ｘ）＞０，Ｇ（ｘ）单调递增 ∴Ｇ（ｘ）≥Ｇ（１）＝０，即 ｘ２ －ｘ≥ｌｎｘ，∴ｘ－１≥ｌｎｘ ｘ即 ｘ－１≥ｆ（ｘ）　② 由①②得 ｇ（ｘ）≥ｆ（ｘ） １２分……………………………………………………………… （方法二）令 ｈ（ｘ）＝ｘｅｘ ｅ －ｘ－ｌｎｘ，ｘ＞０， 则 ｈ′（ｘ）＝ｘｅｘ＋ｅｘ ｅ －１－１ ｘ＝（ｘ＋１）ｅｘ ｅ －ｘ＋１ ｘ ＝（ｘ＋１） ｅｘ－１ －１( )ｘ ， ７分……………… 令 Ｈ（ｘ）＝ｅｘ－１ －１ ｘ，易知 Ｈ（ｘ）在（０，＋∞）上单增，且 Ｈ（１）＝０， 所以当 ０＜ｘ＜１时，Ｈ（ｘ）＜０，从而 ｈ′（ｘ）＜０； 当 ｘ＞１时，Ｈ（ｘ）＞０，从而 ｈ′（ｘ）＞０， 即 ｈ（ｘ）在（０，１）单减，在（１，＋∞）单增， 则 ｈ（ｘ）的最小值为 ｈ（１）＝０， １０分……………………………………………………… 所以当 ｘ＞０时，ｈ（ｘ）≥ｈ（１）＝０，即ｘｅｘ ｅ－ｘ－ｌｎｘ≥０， ｅｘ ｅ≥ｌｎｘ ｘ＋１，即 ｅｘ－１ －１≥ｌｎｘ ｘ，∴ｇ（ｘ）≥ｆ（ｘ） １２分……………………………………… （方法三）记 Ｆ（ｘ）＝ｅｘ－ｅｘ，则 Ｆ′（ｘ）＝ｅｘ－ｅ， 显然 Ｆ′（１）＝０，且 ｘ＜１时，Ｆ′（ｘ）＜０，Ｆ（ｘ）单调递减， ｘ＞１时，Ｆ′（ｘ）＞０，Ｆ（ｘ）单调递增， 所以 Ｆ（ｘ）ｍｉｎ＝Ｆ（１）＝０，故 Ｆ（ｘ）≥０，等号成立当且仅当 ｘ＝１ 故ｅｘ ｅ≥ｘ，等号成立当且仅当 ｘ＝１ ８分…………………………………………………… 欲证 ｅｘ－１ －１≥ｌｎｘ ｘ，只需证明 ｘ≥ｌｎｘ ｘ＋１，即 ｘ２ －ｘ－ｌｎｘ≥０ 记 Ｇ（ｘ）＝ｘ２ －ｘ－ｌｎｘ，则 Ｇ′（ｘ）＝２ｘ－１－１ ｘ＝（ｘ－１）（２ｘ＋１） ｘ 从而 ０＜ｘ＜１时，Ｇ′（ｘ）＜０，Ｇ（ｘ）单调递减， ｘ＞１时，Ｇ′（ｘ）＞０，Ｇ（ｘ）单调递增， 所以，Ｇ（ｘ）ｍｉｎ＝Ｇ（１）＝０，可得 Ｇ（ｘ）≥０，即 ｅｘ－１ －１≥ｌｎｘ ｘ， ∴ｇ（ｘ）≥ｆ（ｘ） １２分……………………………………………………………………… （以上答案仅供参考，其它解法请参考以上评分标准酌情赋分） ）页４共（页４第准标分评及案答考参）类工理（学数级年三高市埠蚌