七年级下数学课件：第五章 相交线与平行线（小结） （共17张PPT）_人教新课标

七年级下数学课件：第五章 相交线与平行线（小结） （共17张PPT）_人教新课标

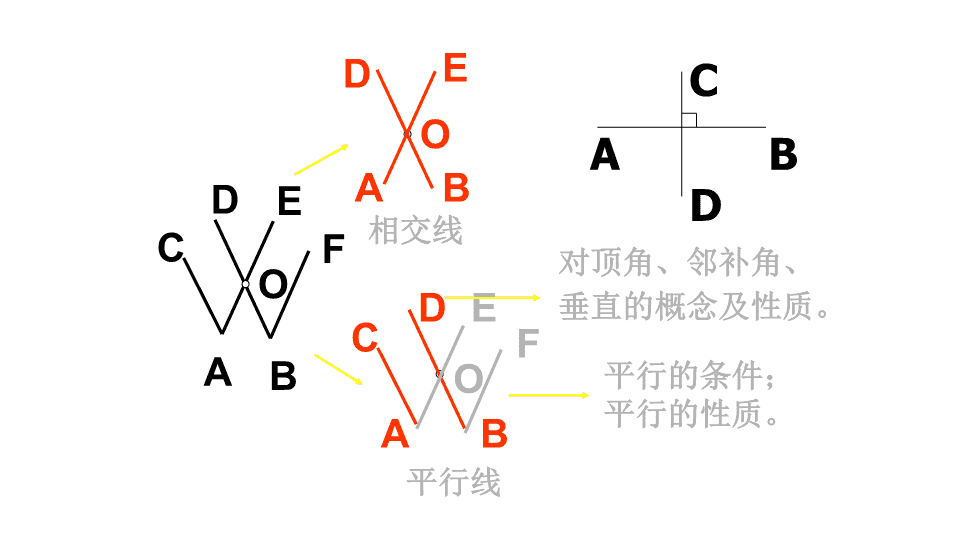
回顾与思考 第五章相交线与平行线 A B C D E F O A B C D A B D E O 相交线 F E O 平行线 对顶角、邻补角、 垂直的概念及性质。 平行的条件； 平行的性质。 A B C D 1、有公共顶点，两边互为反向延长线的两个 角叫做_______。 2、对顶角_____。 对顶角 相等 概念、性质填空： 3、过一点 与已知直线垂直。有且只有一条直线 4、连接直线外一点与直线上各点的所有 线段中， .垂线段最短 .5、对某一事情作出______的语句, 叫做命题. 6、命题是由_______和______两部分组成. 判断 题设 结论 “三线八角” • 两直线被第三直线所截, 平行线的判定方法： 平行线的性质： §两直线平行，同位角相等； §两直线平行，内错角相等； §两直线平行，同旁内角互补。 •同位角相等，两直线平行； •内错角相等，两直线平行； •同旁内角互补，两直线平行； •平行于同一直线的两直线平行。 8 7 6 5 4 3 2 1 a b ∵∠1=∠5 ∴a∥b ∵∠3=∠5 ∴a∥b ∵∠2+∠5=180 ∴a∥b 。 相 交 线 与 平 行 线 相 交 线 平 行 线 垂直、对顶角 丰 富 情 景 探索直线平 行的性质 探索直线平 行的条件 同位角 内错角 同旁内角 本章知识结构图： 二、强化知识、技能训练 a dc b 3 1 2 1.如图，以下是某位同学 作业中的一段说理： 如果∠1=∠2 ，那么 根据同位角相等，两直线平行， 可得a∥b； 如果∠2+∠3=180 °，那么 根据两直线平行，同旁内角互补， 可得c∥d。你认为他说得对吗？ ___ ___ ______________ E 3 OA B C D 2 1 2.若∠BOC=2∠1， 则∠1=______， ∠BOC=_______。 34° 60° 120 ° 若OE⊥AB ,∠1=56°, 则∠3=_____。 3.如图，在甲、乙两地之间 要修一条笔直的公路，从 甲地测得公路的走向是北 偏东42 °.甲、乙两地同 时开工，若干天后公路准 确接通，乙地所修公路的 走向是南偏西多少度？为 什么？ 甲 乙 北 北 42 ° 南偏西42 ° 4.如图是举世闻名的三星堆考古中发掘出 的一个梯形残缺玉片，工作人员从玉片上 已经量得∠A=115°，∠D=110°。已知梯 形的两底AD//BC，请你求出另外两个角的 度数。（学生尝试用自己的方式书写说理 过程） A D B C 115° 110°∠A=115° ∠B=65 ° ∠D=110° ∠C=70 ° 三、运用本章知识、技能 解决一些简单问题： 1.（算算看）已知如图， OB⊥OA，直线CD过O， ∠BOD=110°， 求∠AOC的度数？ A C B D O ∠BOD=110° ∠BOC=70° ∠AOC=20° 2.(考考你)图中如果AC∥BD 、 AE ∥BF ，那么∠A与∠B的关系 如何？你是怎样思考的？ AC∥BD， AE ∥BFA B C D E F O ∠A=∠B ∠A=∠DOE ∠B=∠DOE ∠A=∠B 3.(辨析与比较)如图，是两块相同 的三角尺拼接成的一个图形，请找 出图中互相平行的边。 ∠1= ∠2 A1D∥BC1 ∠3= ∠4 AB∥CD 若其中一块三角尺沿着重合的边向 下滑动（如图所示），原来平行的 边还平行吗？你知道其中的道理吗？ A B C D1 2 4 3 C A1 B D A C1 13 2 4 A B C D E 1 F 2 4.（操作与解释）如图，以点B为顶点, 射线BC为一边，利用尺规作∠EBC，使 得∠EBC=∠A，EB与AD一定平行吗？ 四.拓展——探索与思考： v有一条长方形纸带，按如图所示 沿AB折叠时，当∠1=30°求纸带 重叠部分中∠CAB的度数。 A BC1 2 3 4 E F ∠CAB =75° 如图,已知AB∥CD, (1)若∠ABE=28°,∠CDE=42°,求∠BED的度数. (2)若点E的位置如图(1)(2)(3)变化后,探索∠BED, ∠ABE,∠CDE之间的数量关系. DC B E A 28° 42° C D C A E (1) B D B A E (2) DC A B E (3) 解：画EG∥AB，所以∠B＝∠BEG= 28°， ∵ AB∥CD ∴ EG∥CD，∴∠GED=∠D= 42° ∴∠BED=∠BEG+ ∠GED= 28°+ 42°= 70° G 答：它们的关系分别是： ①∠BED + ∠ABE + ∠CDE = 360° ② ∠BED + ∠ABE = ∠CDE ③ ∠BED + ∠CDE = ∠ABE 课外作业： 独立完成一份小结，用自己的语言 梳理本章内容，并回顾自己在本章学 习中的收获、困难和需要改进的地方。