- 2021-04-20 发布 |
- 37.5 KB |
- 30页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习专题五功 功率 动能定理课件(30张)(全国通用)
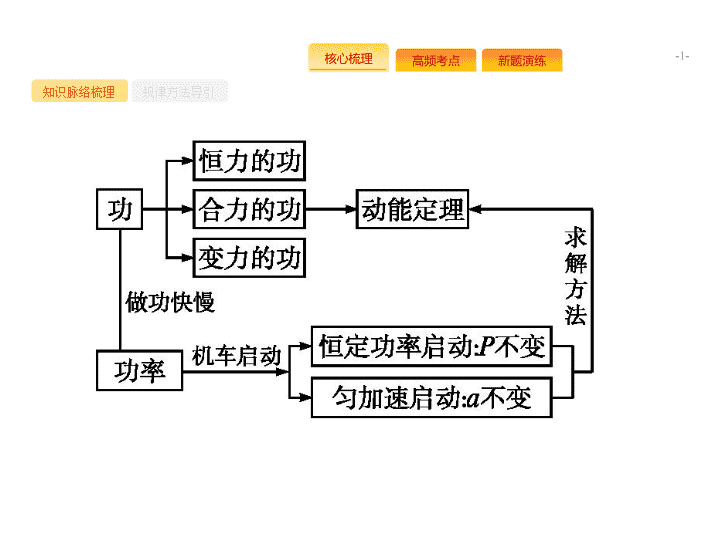
- 1 - 知识脉络梳理 规律方法导引 - 2 - 知识脉络梳理 规律方法导引 - 3 - 命题热点一 命题热点二 命题热点三 功、功率的理解与计算 常以选择题形式考查功、功率的基本公式。 例 1 ( 不定项 ) 质量为 m= 2 kg 的物体沿水平面向右做直线运动 , t= 0 时刻受到一个水平向左的恒力 F , 如图甲所示 , 此后物体的 v - t 图象如图乙所示 , 取水平向右为正方向 , g 取 10 m/s 2 , 则 ( ) A. 物体与水平面间的动摩擦因数为 μ= 0 . 5 B.10 s 末恒力 F 的瞬时功率为 6 W C.10 s 末物体在计时起点左侧 2 m 处 D.10 s 内物体克服摩擦力做功 34 J CD - 4 - 命题热点一 命题热点二 命题热点三 解析 由题图乙知前后两段时间内物体加速度的大小分别为 a 1 = 2 m/s 2 、 a 2 = 1 m/s 2 , 由牛顿第二定律知 F+μmg=ma 1 , F-μmg=ma 2 , 联立得 F= 3 N 、 μ= 0 . 05,A 错误 ;10 s 末恒力 F 的瞬时功率为 P=Fv= 18 W,B 错误 ; 由速度图象与坐标轴所围面积的物理意义知 ,10 s 内物体的位移 x=- 2 m, 即在计时起点左侧 2 m 处 ,C 正确 ;10 s 内物体的路程为 s= 34 m, 即 10 s 内物体克服摩擦力所做的功 W=μmgs= 0 . 05 × 2 × 10 × 34 J = 34 J,D 正确。 - 5 - 命题热点一 命题热点二 命题热点三 思维导引 - 6 - 命题热点一 命题热点二 命题热点三 规律方法关于功、功率应注意的三个问题 (1) 功的公式 W=Fl 和 W=Fl cos α 仅适用于恒力做功的情况。 (2) 变力做功的求解要注意对问题的正确转化 , 如将变力转化为恒力 , 也可应用动能定理等方法求解。 (3) 对于功率的计算 , 应注意区分公式 和公式 P=Fv , 前式侧重于平均功率的计算 , 而后式侧重于瞬时功率的计算。 - 7 - 命题热点一 命题热点二 命题热点三 拓展训练 1 (2017· 全国 Ⅲ 卷 ) 如图所示 , 一质量为 m , 长度为 l 的均匀柔软细绳 PQ 竖直悬挂。用外力将绳的下端 Q 缓慢地竖直向上拉起至 M 点 , M 点与绳的上端 P 相距 。重力加速度大小为 g 。在此过程中 , 外力做的功为 ( ) A - 8 - 命题热点一 命题热点二 命题热点三 机车启动问题 常以选择题的形式考查机车的两种启动方式 , 及学生对实际物理问题的逻辑推理能力。 例 2 ( 不定项 ) 某电动汽车在平直公路上从静止开始加速 , 测得发动机功率随时间变化的图象和其速度随时间变化的图象分别如图甲、乙所示 , 若电动汽车所受阻力恒定 , 则下列说法正确的是 ( ) A. 测试时该电动汽车所受阻力为 1 . 0 × 10 3 N B. 该电动汽车的质量为 1 . 2 × 10 3 kg C. 在 0 ~ 110 s 内该电动汽车的牵引力做功为 4 . 4 × 10 6 J D. 在 0 ~ 110 s 内该电动汽车克服阻力做的功为 2 . 44 × 10 6 J ABD - 9 - 命题热点一 命题热点二 命题热点三 - 10 - 命题热点一 命题热点二 命题热点三 思维导引 - 11 - 命题热点一 命题热点二 命题热点三 规律方法解决机车启动问题时应注意的问题 (1) 分清是匀加速启动还是恒定功率启动。 (2) 匀加速启动过程中 , 机车功率是不断改变的 , 但该过程中的最大功率是额定功率 , 匀加速运动阶段的最大速度小于机车所能达到的最大速度 , 达到额定功率后做加速度减小的加速运动。 (3) 以额定功率启动的过程中 , 机车做加速度减小的加速运动 , 速度最大值等于 , 牵引力是变力 , 牵引力做的功 W=Pt 。 - 12 - 命题热点一 命题热点二 命题热点三 拓展训练 2 一汽车在平直公路上行驶。从某时刻开始计时 , 发动机的功率 P 随时间 t 的变化如图所示。假定汽车所受阻力的大小 F f 恒定不变。下列描述该汽车的速度 v 随时间 t 变化的图线中 , 可能正确的是 ( ) A - 13 - 命题热点一 命题热点二 命题热点三 拓展训练 3 ( 不定项 ) (2017· 云南曲靖模拟 ) 一辆汽车在平直的公路上运动 , 运动过程中先保持某一恒定加速度 , 后保持恒定的牵引功率 , 其牵引力和速度的图象如图所示。若已知汽车的质量 m , 牵引力 F 1 和速度 v 1 及该车所能达到的最大速度 v 3 , 运动过程中所受阻力恒定 , 则根据图象所给的信息 , 下列说法正确的是 ( ) AD - 14 - 命题热点一 命题热点二 命题热点三 动能定理的应用 常以选择、计算题的形式考查学生利用动能定理处理复杂过程的能力。 - 15 - 命题热点一 命题热点二 命题热点三 例 3 如图所示 , 足够长的木板静止在粗糙的水平地面上 , 木板的质量 m 0 = 2 kg, 与地面间的动摩擦因数 μ 1 = 0 . 1; 在木板的左端放置一个质量 m= 2 kg 的小铅块 ( 视为质点 ), 小铅块与木板间的动摩擦因数 μ 2 = 0 . 3 。现给铅块一向右的初速度 v 0 = 4 m/s, 使其在木板上滑行 , 木板获得的最大速度 v= 1 m/s, g 取 10 m/s 2 , 求 : (1) 木板达到最大速度时 , 木板运动的位移 ; (2) 铅块与木板间因摩擦产生的总热量 ; (3) 整个运动过程中木板对铅块的摩擦力所做的功。 答案 (1)0 . 5 m (2)12 J (3) - 16 J - 16 - 命题热点一 命题热点二 命题热点三 - 17 - 命题热点一 命题热点二 命题热点三 思维导引 - 18 - 命题热点一 命题热点二 命题热点三 例 4 如图所示,在一倾角为37 ° 的绝缘斜面下端 O ,固定有垂直于斜面的绝缘挡板。斜面 ON 段粗糙,长度 s= 0 . 02 m, NM 段光滑,长度 l= 0 . 5 m。在斜面所在的区域有竖直向下的匀强电场,电场强度为2 × 10 5 N/C。有一小滑块质量为2 × 10 - 3 kg,带正电,电荷量为1 × 10 - 7 C,小滑块与 ON 段表面的动摩擦因数为0 . 75。将小滑块从 M 点由静止释放,在运动过程中没有电荷量损失,与挡板相碰后原速返回。已知sin 37 ° = 0 . 6,cos 37 ° = 0 . 8, g 取10 m/s 2 。求 : (1)小滑块第一次过 N 点的速度大小; (2)小滑块最后停在距离挡板多远的位置。 - 19 - 命题热点一 命题热点二 命题热点三 解析 (1) 小滑块第一次过 N 点的速度为 v , 则由动能定理有 (2) 滑块在 ON 段运动时所受的摩擦力 F f =μ ( mg cos 37 ° +qE cos 37 ° ) = 2 . 4 × 10 - 2 N 滑块所受重力、电场力沿斜面的分力 F 1 =mg sin 37 ° +qE sin 37 ° = 2 . 4 × 10 - 2 N 因此滑块沿 ON 下滑时做匀速运动 , 上滑时做匀减速运动 , 速度为 0 时可停下。设小滑块与挡板碰撞 n 次后停在距挡板距离为 x 处 , 则由动能定理得 ( mg+qE )( l+s-x )sin 37 ° -μ ( mg+qE )[(2 n- 1) s+x ]cos 37 ° = 0 由 0 ≤ x ≤ 0 . 02 m 得 12 . 5 ≤ n ≤ 13 . 5 取 n= 13 得 x= 0 . 01 m 。 - 20 - 命题热点一 命题热点二 命题热点三 思维导引 - 21 - 命题热点一 命题热点二 命题热点三 规律方法 1 . 电场力做功与重力做功的特点类似 , 都与路径无关。 2 . 对于电场力做功或涉及电势差的计算 , 选用动能定理往往最简便快捷 , 但运用动能定理时要特别注意运动过程的选取。 3 . 应用动能定理解题的基本步骤 : - 22 - 命题热点一 命题热点二 命题热点三 拓展训练 4 (2017· 山东莱州模拟 ) 如图所示 , 用内壁光滑的薄壁细管弯成的 “S” 形轨道固定于竖直平面内 , 其弯曲部分是由两个半径均为 R= 0 . 2 m 的半圆平滑对接而成 ( 圆的半径远大于细管内径 ), 轨道底端 D 点与粗糙的水平地面相切。现有一辆质量为 m= 1 kg 的玩具小车以恒定的功率从 E 点由静止开始出发 , 经过一段时间 t= 4 s 后 , 出现了故障 , 发动机自动关闭 , 小车在水平地面继续运动并进入 “S” 形轨道 , 从轨道的最高点飞出后 , 恰好垂直撞在固定斜面 B 上的 C 点 , C 点与下半圆的圆心 O 等高。已知小车与地面之间的动摩擦因数为 μ= 0 . 1, ED 之间的距离为 x 0 = 10 m, 斜面的倾角为 30 ° 。求 :( g 取 10 m/s 2 ) - 23 - 命题热点一 命题热点二 命题热点三 (1) 小车到达 C 点时的速度大小 ; (2) 在 A 点小车对轨道的压力大小是多少 , 方向如何 ; (3) 小车的恒定功率。 答案 (1)4 m/s (2)10 N 方向竖直向上 (3)5 W - 24 - 命题热点一 命题热点二 命题热点三 - 25 - 1 2 3 4 5 1 . ( 不定项 ) 如图所示 , 足够长的传送带与水平方向的倾角为 θ , 物块 a 通过平行于传送带的轻绳跨过光滑轻滑轮与物块 b 相连 , b 的质量为 m 。开始时 , a 、 b 及传送带均静止 , 且 a 不受传送带摩擦力作用 , 现让传送带逆时针匀速转动 , 则在 b 上升 h 高度 ( 未与滑轮相碰 ) 过程中 ( ) A. 物块 a 的重力势能减少 mgh B. 摩擦力对 a 做的功等于 a 机械能的增量 C. 摩擦力对 a 做的功等于物块 a 、 b 动能增量之和 D. 任意时刻 , 重力对 a 、 b 做功的瞬时功率大小相等 ACD - 26 - 1 2 3 4 5 2 . ( 不定项 ) 如图所示 , 一辆货车通过光滑轻质定滑轮提升一箱货物 , 货箱质量为 m 0 , 货物质量为 m , 货车以速度 v 向左匀速运动 , 将货物提升高度 h , 则 ( ) A. 货物向上做匀速运动 B. 箱中的物体对箱底的压力大于 mg C. 图示位置时货车拉力的功率大于 ( m 0 +m ) gv cos θ D. 此过程中货车拉力做的功为 ( m 0 +m ) gh BC - 27 - 1 2 3 4 5 3 . 如图所示 , 一半径为 R 、粗糙程度处处相同的半圆形轨道竖直固定放置 , 直径 POQ 水平。一质量为 m 的质点自 P 点上方高度 R 处由静止开始下落 , 恰好从 P 点进入轨道。质点滑到轨道最低点 N 时 , 对轨道的压力为 4 mg , g 为重力加速度的大小。用 W 表示质点从 P 点运动到 N 点的过程中克服摩擦力所做的功。则 ( ) C - 28 - 1 2 3 4 5 4 . (2017· 辽宁铁岭模拟 ) 如图所示 , 竖直平面内放一直角杆 MON , OM 水平 , ON 竖直且光滑 , 用不可伸长的轻绳相连的两小球 A 和 B 分别套在 OM 和 ON 杆上 , B 球的质量为 2 kg, 在作用于 A 球的水平力 F 的作用下 , 球 A 、 B 均处于静止状态 , 此时 OA= 0 . 3 m, OB= 0 . 4 m 。改变水平力 F 的大小 , 使 A 球向右加速运动 , 已知 A 球向右运动 0 . 1 m 时速度大小为 3 m/s, 则在此过程中绳对 B 球的拉力所做的功为 ( g 取 10 m/s 2 ) ( ) A.11 J B.16 J C.18 J D.9 J C - 29 - 1 2 3 4 5 (1) 求小球在 B 、 A 两点的动能之比。 (2) 通过计算判断小球能否沿轨道运动到 C 点。 答案 (1)5 ∶ 1 (2) 见解析 - 30 - 1 2 3 4 5查看更多