人教版9年级下册数学精品示范教案27_3 位似（1）

人教版9年级下册数学精品示范教案27_3 位似（1）

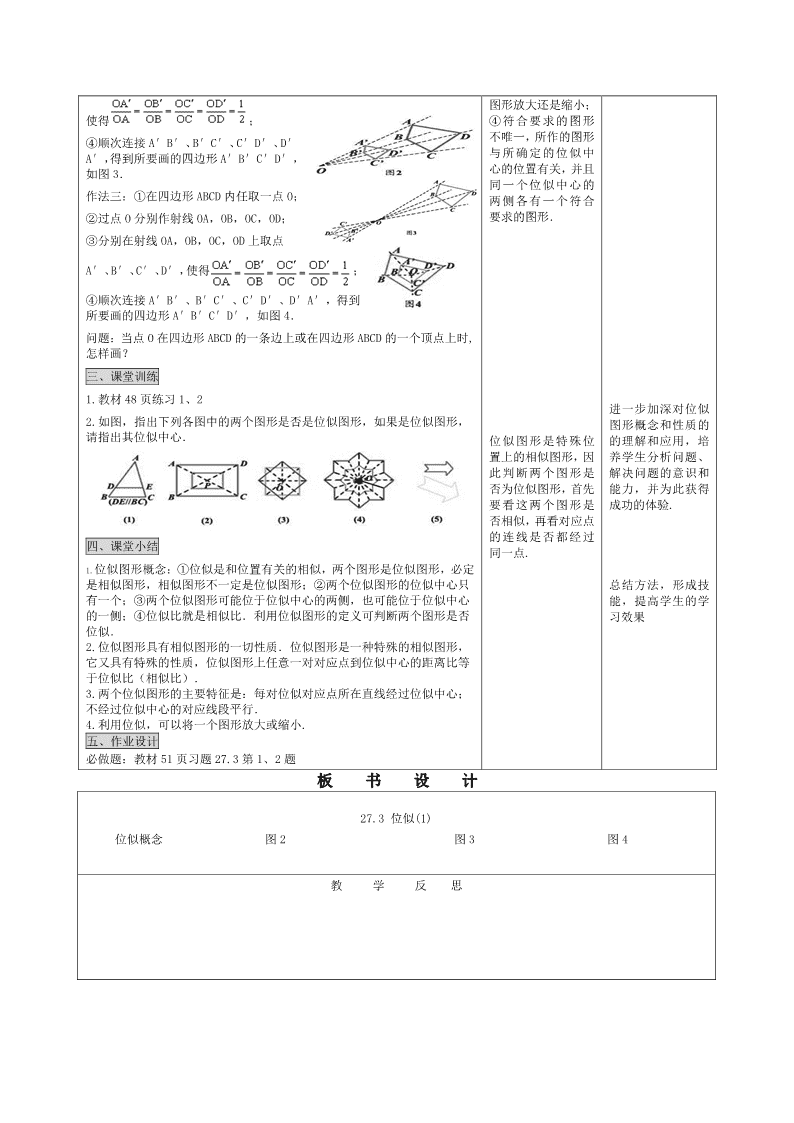
年级 九 年 级 课题 27.3 位似(1) 课型 新授 教 学 媒 体 多 媒 体 教 学 目 标 知识 技能 1.了解位似图形及其有关概念，了解位似与相似的联系和区别，掌握位似图形的性质； 2．掌握位似图形的画法，能够利用作位似图形的方法将一个图形放大或缩小．1 过程 方法 通过设置问题情境，建立数学概念，解释、应用与拓展，引导学生观察、验证，推理，交流，探究 位似变换和图形缩放. 情感 态度 发展学生的探究能力，培养学生多种感官并用的良好学习习惯，增强数学应用意识与能力. 教 学 重 点 位似图形的有关概念、性质与作图. 教 学 难 点 利用位似将一个图形放大或缩小． 教 学 过 程 设 计 教 学 程 序 及 教 学 内 容 师生行为 设 计 意 图 一、情景引入 1．观察：在日常生活中，我们经常见到下面所给的这样一类相似的图形， 它们有什么特征？ 这样的放大或缩小，没有改变图形的形状，经过放大或缩小的图形与原 图形是相似的. 引出课题：这节课来探究这类问题. 二、自主探究 （一）概念 右图中有相似多边形吗？如果有， 这种相似有什么特征？ 每幅图中的两个多边形不仅相似，而且对应顶点的连线相交于一点，像这 样的两个图形叫做位似图形，这个点叫做位似中心．这时的相似比又叫位 似比. （二）利用位似可以将一个图形放大或缩小 把图 1 中的四边形 ABCD 缩小到原来的 ． 分析：把原图形缩小到原来的 ，也就是使新图形上各顶点到位似中心的 距离与原图形各对应顶点到位似中心的距离之比为 1∶2． 作法一：①在四边形 ABCD 外任取一点 O； ②过点 O 分别作射线 OA，OB，OC，OD； ③分别在射线 OA，OB，OC，OD 上取点 A′、B′、C′、D′ 使得 ； ④顺次连接 A′B′、B′C′、C′D′、D′A′，得到四边形 A′B′C′D′， 如图 2． 问：此题还可以如何画出图形？ 作法二：①在四边形 ABCD 外任取一点 O； ②过点 O 分别作射线 OA， OB， OC，OD； ③分别在射线 OA， OB， OC， OD 的反向延长线上取点 A′、B′、C′、D′， 教师提出问题，引入 新课，学生观察，思 考. 教师给出图形，让学 生观察，进行猜想， 探究，交流，归纳， 尝试得出位似图形 的特征.教师给出明 确的相关概念. 教师布置任务，学生 以小组形式完成.通 过画图，证明，师生 总结出画位似图形 的一般步骤： ①首先确定位似中 心，位似中心的位置 可随意选择；②确定 原图形的关键点，如 四边形有四个关键 点，即它的四个顶 点；③确定位似比， 根据位似比的取值， 可以判断是将一个 培养学生的观察能 力与想象力，形象 的引入课题. 提高学生观察能 力，分析解决问题能 力，加强小组活动的 效果. 培养学生的作图能 力和语言表达能力， 拓宽学生思维，让学 生 总 结解 决问 题 的 多 种 方法 ，触 类 旁 通，获得成功体验， 增强学习信心. 35 板 书 设 计 使得 ； ④顺次连接 A′B′、B′C′、C′D′、D′ A′，得到所要画的四边形 A′B′C′D′， 如图 3． 作法三：①在四边形 ABCD 内任取一点 O； ②过点 O 分别作射线 OA，OB，OC，OD； ③分别在射线 OA，OB，OC，OD 上取点 A′、B′、C′、D′，使得 ； ④顺次连接 A′B′、B′C′、C′D′、D′A′，得到 所要画的四边形 A′B′C′D′，如图 4． 问题：当点 O 在四边形 ABCD 的一条边上或在四边形 ABCD 的一个顶点上时, 怎样画？ 三、课堂训练 1.教材 48 页练习 1、2 2.如图，指出下列各图中的两个图形是否是位似图形，如果是位似图形， 请指出其位似中心． 四、课堂小结 1.位似图形概念：①位似是和位置有关的相似，两个图形是位似图形，必定 是相似图形，相似图形不一定是位似图形；②两个位似图形的位似中心只 有一个；③两个位似图形可能位于位似中心的两侧，也可能位于位似中心 的一侧；④位似比就是相似比．利用位似图形的定义可判断两个图形是否 位似． 2.位似图形具有相似图形的一切性质．位似图形是一种特殊的相似图形， 它又具有特殊的性质，位似图形上任意一对对应点到位似中心的距离比等 于位似比（相似比）． 3.两个位似图形的主要特征是：每对位似对应点所在直线经过位似中心； 不经过位似中心的对应线段平行． 4.利用位似，可以将一个图形放大或缩小. 五、作业设计 必做题：教材 51 页习题 27.3 第 1、2 题 图形放大还是缩小； ④符合要求的图形 不唯一，所作的图形 与所确定的位似中 心的位置有关，并且 同一个位似中心的 两侧各有一个符合 要求的图形． 位似图形是特殊位 置上的相似图形，因 此判断两个图形是 否为位似图形，首先 要看这两个图形是 否相似，再看对应点 的连线是否都经过 同一点. 进一步加深对位似 图形概念和性质的 的理解和应用，培 养学生分析问题、 解决问题的意识和 能力，并为此获得 成功的体验. 总结方法，形成技 能，提高学生的学 习效果 27.3 位似(1) 位似概念 图 2 图 3 图 4 教 学 反 思